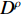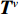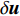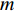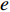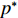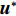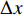Research progress of smoothed particle hydrodynamics and its applications in high-speed hydrodynamic problems
-
摘要: 船海工程领域中的高速水动力问题及其涉及的复杂流−固耦合过程普遍具有大变形、动边界、强对流、多介质等特征，一直是研究的热点和难点。而传统的网格算法在捕捉边界或界面大变形时存在一定局限性，亟待开发新一代无网格数值模拟技术。其中，光滑粒子流体动力学（SPH）作为拉格朗日无网格粒子方法，在捕捉多相界面和流−固耦合界面时具有较高的精度和强鲁棒性。近年来，随着SPH理论及方法的不断完善，SPH在理论完备性及计算稳定性方面取得了许多新的进步和突破，在模拟高速水动力方面的优势不断凸显，开始广泛应用于船海工程问题。为此，围绕水面航行器的高速水动力、航行体的跨介质水动力、水下爆炸与结构毁伤等问题，针对SPH理论及方法在上述领域取得的研究进展进行综述，讨论现有方法面临的问题与挑战，并展望未来需要开展的研究工作，旨在为后续相关研究提供参考。Abstract: High-speed hydrodynamics and its corresponding complex fluid-structure interactions (FSI) are challenging topics associated with naval architecture and ocean engineering, typically characterized by large deformations, moving boundaries, strong convection and multiple fluid media. Since traditional mesh-based numerical methods possess limited ability to accurately simulate such strongly nonlinear problems, it is imperative to develop meshless numerical schemes with high fidelity and robustness to tackle this dilemma. As one of the most promising truly meshless methods, smoothed particle hydrodynamics (SPH) shows apparent advantages in high-speed hydrodynamics problems thanks to its Lagrangian nature. In the present paper, the attention is particularly focused on the latest advances of several SPH techniques with respect to the following high-speed hydrodynamics problems: vessel-induced waves and wakes, the water entry process of projectiles, and underwater explosion and its resulting structural damage; in addition, the future prospects of SPH are provided in the last part of the paper.
-
0. 引 言
面向海洋强国的战略需要，船舶与海洋工程得到了大力发展，与之相关的结构力学和水动力学等领域均产出了丰硕成果[1-3]。其中，高速舰船兴波[4]、航行体（器）出水与入水[5]、水下爆炸与结构毁伤[6-7]等典型高速水动力学问题与现代舰船及其武器装备的综合性能密切相关，但这些问题都具有大变形、动边界、强对流、多介质等复杂特征，而运用传统理论、试验或数值模拟方法较难得到彻底解决，因此，近年来成为了研究热点和难点[8-9]。
高速水面航行器的兴波、飞机水上滑行等过程涉及了复杂曲面结构物与自由液面或水气界面的复杂耦合作用，剧烈的液固耦合运动易产生非线性翻卷和破碎波浪[10]，甚至会引起液滴强烈飞溅，对航行器的结构及内部仪器零件的安全性构成威胁，且诱导的噪声[11]和尾迹[12-13]对航行器隐蔽性极为不利，精准捕捉兴波水花飞溅和预报砰击载荷关系到航行器的隐身性、安全性设计。
在军民用领域中，抛落式救生艇入水、飞行器海上回收，鱼雷空投入水、潜射导弹出水等航行器或结构物高速出、入水的问题[14-15]涉及瞬态强冲击载荷、结构物大幅运动、气泡生长与溃灭等复杂过程[16]，是典型的多相流−固耦合问题[17]。这种高速跨介质过程所产生的巨大砰击载荷，一方面可能造成装备结构损坏、内部零件失灵，另一方面也可能引起航行器弹道失稳、投放失效等。因此，研究航行器的高速出、入水问题对于跨介质武器装备等的研发有着重要意义。
研究表明，水下爆炸冲击波峰值及冲量相比空中爆炸有明显提高[18]。舰船遭受近场水下爆炸时，冲击波、高速射流和破片等首先对舰船造成局部毁伤[19]，随后的气泡脉动和射流冲击可能造成舰船整体失效[7]。近场水下爆炸导致船体出现破口以后，剧烈涌流还可能会进一步造成船体结构损坏，最终导致船体沉没。考虑到水下爆炸过程的复杂性和试验研究的高成本，研发精准的数值计算方法，预报水下爆炸载荷、结构毁伤和舰船破损沉没过程成为了各国海军研究的重点[19]。
对于上述高速航行器的兴波、航行体出水和入水、水下爆炸与结构毁伤等工程问题，其背后的基础力学问题离不开对复杂运动结构物与多相流体之间的流−固耦合过程的求解。研究人员针对不同场景下的力学过程进行简化和凝练，提出了多种理论模型[20-21]，解释了气泡动力学或简单构型结构物与流体作用过程背后的力学机理。然而，理论模型对于复杂的工程实际问题适用性有限。而模型试验虽然是获得可靠结果的重要手段[4, 22]，但开展试验通常需要较大的场地和昂贵的设备，尤其是在高速水动力问题的模型试验中，尺度效应明显[23]，相关物理参数测量困难，试验数据的可重复性较差，试错成本也高。
近年来，随着计算机技术的发展，涌现出了许多数值计算方法。目前，基于不同的离散和求解形式，数值模拟方法可分为有网格法和无网格法[24]。前者在解决大变形流−固耦合问题时容易受到网格畸变的困扰；后者得益于天然的拉格朗日特性及逐渐完备的粒子近似理论优势，在模拟大变形问题时不受边界变形量的限制[25]，故在高速水动力问题中得到了广泛应用[24]。典型的无网格法包括离散元法（discrete element method, DEM）[26]、光滑粒子流体动力学（smoothed particle hydrodynamics, SPH）方法[27-29]、移动粒子半隐式（moving particle semi-implicit）方法[30]等。MPS方法和SPH方法在求解水动力问题方面难分伯仲[31-34]，但MPS方法基于完全不可压缩假设[35-36]，难以应用于压缩效应明显的问题，例如水下爆炸的气泡脉动过程等；而DEM是离散元算法[37]，主要用于处理离散粒子（例如沙砾、冰块等颗粒流）大变形问题[38-40]，并不适用于高速水力学研究。相较而言，SPH理论和方法在处理流体大变形和可压缩问题时的优势明显，便于开展并行计算，工程适用性强，更适合于求解大型高速水动力问题。
海洋结构物在高速航行或跨介质运动时，对自由液面以下的单相流动区域，准确模拟湍流边界层是关键[41]。针对这方面的应用，有网格法因其湍流模型较为成熟、便于采用多分辨率网格技术而受到研究人员的青睐[42]。但对于自由液面或多相界面附近区域，因存在流体高速砰击引起的液滴飞溅和水气掺混等过程，有网格法的精度容易受到网格尺度的极大限制[24]。例如，一旦液滴飞溅到网格稀疏区域，易引起流体质量不守恒造成的液滴飞溅消失。相比而言，SPH无网格粒子法用于模拟液滴飞溅问题更具优势[4, 22]。该方法基于核近似、粒子近似和虚粒子边界等基本原理，辅之以日益完善的高精度修正理论和技术，在模拟运动边界和大变形界面等问题时具有较强计算能力和广阔发展前景。
尽管SPH方法在计算的全过程中能够精确满足质量守恒要求并擅长捕捉自由液面翻卷、破碎和喷溅等复杂现象，但运用传统SPH方法计算的压力载荷一般伴随严重的数值噪声[43]，涉及复杂区域时还容易引起张力不稳定性和数值空洞等[44]。为解决这些问题，经过近半个世纪的不断发展，SPH方法在理论和数值技术方面得到了不断优化，计算精度和稳定性获得巨大提升，在新一代GPU并行技术的加持下，显著提高了计算效率[45]，具备了求解工程问题的能力。并且，随着嵌入SPH的多算法耦合技术的出现和发展[6, 46-47]，SPH理论和方法的优势得以充分发挥，使其为复杂多元的高速水动力学问题提供了新的高精度、高效率求解方案。
综上所述，为进一步阐述SPH理论和方法在船海高速水动力学相关问题中的研究进展，本文将从SPH的基本原理及数值技术研究进展出发，围绕高速水面航行器的水动力以及高速跨介质航行器水动力问题、水下爆炸与结构毁伤等方面展开综述，并对SPH理论和方法在求解高速水动力问题中的未来发展趋势进行展望，以期为涉及上述问题的相关研究提供参考。
1. SPH理论及技术进展
1.1 SPH基本理论与算法
1.1.1 SPH基本理论
SPH方法最初是为研究天体动力学而提出的[48]，上世纪90年代开始应用于水动力问题的模拟[49]。以物体入水问题为例，图1给出了基于流体体积（volume of fluid，VOF）的欧拉网格法[50]及拉格朗日描述的SPH方法[51-52]模拟圆柱体及楔形体入水以及液面飞溅的过程。在欧拉网格法的计算结果中，可见喷溅射流尖端存在非物理性流体消失，水气界面较模糊的情况，而SPH方法中粒子可以精确地捕捉到流体飞溅特征。上述结果体现了SPH方法在处理大变形问题方面的优势，因此被广泛应用于船海工程领域[5, 53]。
从原理上看，SPH方法基于核函数近似理论计算空间导数，可对特定物理场的梯度、散度等采用积分形式进行计算[54]；在数值实现方面，SPH方法一般将流体域离散成紧凑的拉格朗日粒子，每个粒子均具有相应的质量和体积，通过粒子求和代替核近似中的积分，也称“粒子近似”。如图2所示，基于核近似理论和粒子近似理论，SPH方法可对控制方程进行离散求解。图中：
f 和\boldsymbol{f} 分别代表标量和矢量；\rho ，\boldsymbol {u} ，p ，\boldsymbol{r} ，V 分别表示密度、速度、压力、位置矢量和体积，下标i 和j 表示粒子编号；\boldsymbol{g} ，\boldsymbol{T} ，\mu 分别表示重力加速度、应力张量和动力黏性系数；W 为核函数；h 为光滑长度；{c_0} ，{\rho _0} 分别为流体声速及其参考密度。为获得更高的压力场、速度场计算精度，可在离散控制方程中进一步添加耗散项[24]。随后，在特定的初始条件和边界条件（自由液面边界[55]、壁面边界[56]、流入流出边界[57]、无反射边界[58]等）下，将离散控制方程在时域内进行积分，可获得SPH控制方程的数值解。![]()
图 1 三维圆柱体和二维楔形体入水数值模拟结果Figure 1. Numerical simulations of water entry of a 2D wedge and a 3D cylinderSPH粒子携带各自的速度、压力、密度等物理量，按照流体质点本身的速度进行拉格朗日运动。这些粒子的运动代表了流体的流动，粒子所到之处也代表了所处位置的流场速度、压力、密度等物理量的变化。鉴于SPH理论和方法的拉格朗日特性及无网格粒子特性，在模拟自由液面流动问题时，自由面的运动学条件不仅能够自动满足[55]，而且也能够自动追踪水气和流−固界面，所以十分适合处理船海工程中的大变形、动边界、多介质和强对流的流体动力学问题[8]。
1.1.2 SPH算法的分类
经过近半个世纪的发展，基于不同的理论框架，SPH方法已发展出了多种形式，主要包含两种类型：弱可压SPH （weakly compressible SPH, WCSPH）方法[43]和不可压SPH （incompressible SPH, ISPH）方法[59]，并已在各自领域得到广泛的应用。对于水介质，一般认为其近似于不可压缩，但为便于求解压力，Monaghan等[49]最早引入了状态方程，如图2所示控制方程中的第4个等式。基于状态方程求解压力时，积分的时间步长受到克朗条件（Courant–Friedrichs–Lewy condition），也即流体声速的极大限制。此外，Monaghan等[49]还提出了弱可压假设，以马赫数小于0.1为标准确定人工声速，确保流体密度变化不大于1%，以此维持流体的近似不可压特性，所以该方法也被称为WCSPH方法。相反，在ISPH方法中，流场的密度保持不变，亦即速度散度处处为0。Cummins和Rudman[59]在SPH方法框架内，建立了每个时间步的泊松压力方程，用于求解压力，并提出了ISPH方法来模拟不可压缩流动问题。但是，ISPH方法涉及大型稀疏矩阵运算和自由液面粒子搜索，计算量相对较大[60-61]，在大规模粒子数量的三维计算中挑战较大。WCSPH相关理论和方法经过近20年的发展，计算精度已得到明显提高，相比于ISPH方法，WCSPH方法涉及的GPU存储量更小，计算效率更高，所以更适合于开源程序的设计。例如DualSPHysics[62]、SPHinXsys[63]等开源程序包，它们均是基于WCSPH理论框架，目前已被广泛应用于模拟三维复杂自由液面流动等问题。
1.2 SPH数值技术的进展
1.2.1 SPH压力计算精度
在船海流体力学中，准确计算压力对流体砰击载荷预报至关重要。传统WCSPH模型计算压力场时，一般会出现难以避免的压力场噪声，其主要原因是：
1） SPH核函数的近似误差和数值离散误差会导致密度场出现波动，微小的密度波动被状态方程放大，变成剧烈的压力场噪声；
2） 因流体的弱可压假设，声速一般会被降低。在出现流体砰击时，砰击位置辐射的压力波以较小的声速在流场中传播，遇到边界时会发生多次反射和叠加，同样也会在流场中表现为压力场噪声。
针对压力场噪声问题，Colagrossi等[43]率先提出SPH密度过滤技术，成功缓解了SPH压力场脉动。Vila[64]通过Riemann求解器来计算粒子间的相互作用，提出了Riemann SPH方法，此方法能够将SPH数值误差和弱可压假设造成的压力脉动进行快速耗散，从而提高压力场的光滑性。Marrone等[56]提出δ-SPH方法并应用于自由液面流动的模拟，该方法引入了密度耗散项
{D^\rho } ，该耗散项起到与Riemann求解器相似的耗散作用，也同样能够提高压力场的计算精度。图3所示的δ-SPH控制方程中，{\boldsymbol{T}}^{v} 表示黏性力张量。相比Riemann SPH方法，δ-SPH方法的优势在于数值耗散量可通过连续方程中的密度耗散项[65]进行定量控制，从而实时监测流体能量的耗散量，这对于SPH数值波浪水池的建立十分有益。1.2.2 SPH粒子均匀化技术
传统SPH理论基础和算法精度很大程度上依赖于粒子分布的均匀性[66]。为此，Nestor等[67]最早提出了粒子位移修正方法（particle shifting techniques，PST），而Lind等[68]将PST方法引入到自由液面计算中，初步解决了ISPH模拟中的粒子不均匀及流场撕裂的问题。如图3中第3个框图所示，Sun等[69-70]将PST技术与δ-SPH进行结合，提出了δ+-SPH方法（其中，
\delta {\boldsymbol{u}} 为修正速度项，m 表示粒子质量），随后又发展出了张力不稳定性控制（tensile instability control, TIC）技术[44]，克服了高负压区域的流场数值空洞问题，并成功应用到中、高雷诺数的黏性边界层流动的模拟中。其后，又进一步建立了满足一致性的δ+-SPH方法，将PST技术中位移修正以修正速度的方式表示，并在控制方程予以考虑，从而解决了早前PST技术造成的自由液面流动中流体体积的非物理性膨胀问题，极大提高了WCSPH理论和方法的精度及稳定性[70]。最近，Antuono和Sun等[66]又建立了任意拉格朗日−欧拉(arbitrary Lagrangian-Eulerian, ALE)形式的δ-ALE-SPH理论与方法，将质量方程和质量数值耗散项{D^m} 引入到控制方程中，提高了ALE算法的稳定性，进一步完善了含粒子位移修正的该SPH理论框架。针对海洋工程应用问题，Lü和Sun等[5, 17]针对液舱的晃荡、物体出水和入水、黏性绕流等问题进行了深入分析，从理论角度指出了此类问题中张力不稳定性产生的原因，有针对性地提出了完备的控制技术，以克服张力不稳定性问题。1.2.3 高精度SPH理论和离散格式
制约SPH方法计算精度的另一个重要原因是，传统SPH理论和方法离散格式本身的精度不够，误差主要来源于核函数近似误差和粒子近似误差，其中后者又被称为数值离散误差。因此，为提高SPH方法的计算精度，研究人员先后提出了修正SPH算法[71]、移动最小二乘算法[72]、有限粒子法[73]以及近两年发展的高阶SPH方法，例如WENO-SPH方法[74]、TENO-SPH方法[75]等。高阶SPH理论是在Riemann SPH的基础上发展而来，其通过引入网格法的高阶计算框架来提高求解精度。如图4所示，在Riemann SPH控制方程中，
e 表示比内能[75]，{p^*} 和{\boldsymbol{u}^*} 分别表示粒子对之间的压力及速度[76]，是Riemann方程求解的中间变量，也是重构框架的作用对象。Meng和Zhang等[75]提出的TENO-SPH理论和方法，有效提高了SPH方法的计算精度和鲁棒性，验证了高阶SPH理论和应用的可行性。此外，为减少离散误差，可通过增加光滑长度与粒子间距的比例系数，来增加核函数半径范围内的粒子数量，达到减小离散误差的目的，使之满足理论要求，提高SPH方法的计算精度，具体详见文献[77]。尽管高精度SPH方法在解决特定问题方面明显提升了计算精度，但在物理量守恒性及算法稳定性上仍有很大的改善空间。对于工程化应用，因涉及了巨大的粒子数量和较长模拟时间，目前仍普遍采用传统的SPH数值离散理论，辅之以δ-SPH或Riemann SPH等数值方法，能够严格保障质量、动量的守恒特性，实现对自由液面流动的长时间的稳定数值模拟。1.2.4 SPH方法的工程应用
随着SPH理论和方法的不断发展，其已被广泛应用于海洋工程领域。事实上，SPH工程化应用的重要前提是其具备了复杂结构物的粒子化建模和离散能力，以及复杂形状边界条件的处理能力。经过数十年的发展，慕尼黑工业大学Zhu等[78]开发出了基于.STL格式文件的粒子化填充算法，并已成功用于复杂构型结构物的粒子化离散。图5所示为飞机模型从CAD到粒子化的离散过程，这为后续的工程化应用研究奠定了良好的基础。基于离散后的粒子，将其设置为虚拟粒子（ghost particle），采用基于固定虚粒子（fixed ghost particle）的固壁边界理论和技术[56, 79]，即可实现固定、运动甚至变形的壁面边界的高精度施加处理[51, 80]。
![]()
图 5 复杂构型结构物的CAD建模和粒子化离散Figure 5. CAD modeling and particle discretization of a complex structure1.2.5 SPH硬件加速技术
在SPH数值计算中，精确反映三维复杂结构物构型通常需要设置精细的粒子分辨率，故也必然导致高昂的计算成本。随着计算机技术的快速发展，硬件并行计算技术的出现极大地提高了SPH方法的计算效率，推动了SPH方法的工程化应用[45, 60]。硬件加速技术一般可基于CPU或GPU两种并行计算框架。绝大部分网格法（例如有限体积法（FVM）等）均采用CPU并行计算，原因是该方法需要求解大型稀疏矩阵和隐式时间积分，并不适合或较难采用GPU并行计算。而弱可压SPH方法作为一种纯拉格朗日粒子方法，其计算原理基于点对点的方式，且时间积分为显式格式，这两个特性决定了SPH方法非常适合用于GPU并行计算。目前，大量文献已表明，在同等模拟规模下SPH方法的GPU并行可比CPU并行在效率上提高1~2个数量级[45]，极大提升了SPH方法的工程实用性，尤其是基于该方法开发的计算软件能够在装有GPU的个人电脑上运行[62]，并不完全依赖于大型超级计算机或服务器，因此在未来工程领域有较大的应用潜力。
当前，实现SPH并行计算首先可基于并行计算框架，自主编制SPH程序，例如Marrone等[22]搭建的MPI-OpenMP混合编程模型，设计了一种新型的三维并行SPH求解器，成功实现了对三维船体兴波的全局仿真，为自主构造SPH并行计算模型提供了参考。此外，还可以采用目前主流的并行SPH开源程序包完成计算，例如SPHinXsys[63]、DualSPHysics[62]等开源程序包，它们均在三维复杂问题应用方面有出色表现[81]，为高精度SPH理论和方法在船海工程中的实际应用提供了强大的计算能力保障。
2. 水面航行器高速水动力问题
随着上述数值技术的发展和应用，运用SPH理论和方法求解实际工程问题的能力得到了不断加强。SPH方法利用其在处理自由液面大变形和喷溅问题方面的优势，可以十分方便地对高速水动力问题开展相关研究。例如，图6展示的是三维SPH方法模拟的“中山大学”号（SYSU）科考船高速航行兴波和飞机水上迫降过程。由图可见，SPH方法准确再现了自由液面的翻卷、破碎、喷溅过程。
![]()
图 6 三维SPH方法模拟的“中山大学”号科考船高速航行兴波和飞机水上迫降Figure 6. 3D SPH simulations of the breaking wave of SYSU research vessel in high-speed and the aircraft ditching process以下将围绕航行器的兴波与非线性波浪砰击等问题，对SPH理论和方法在水面航行器高速水动力问题中的应用研究进展进行综述。
2.1 高速水面航行器兴波
目前，计算流−固耦合问题通常使用有限元法（FEM）、FVM等工业化程度高、应用发展较为成熟的求解器，例如，常使用VOF[82]或Level-Set[83]等方法模拟自由面流动。在单相、小变形、低弗劳德数的情况下，使用以上的网格法模拟航行器的兴波和尾流可以得到精准结果，但对高速航行过程中产生的强非线性自由液面流动、流体喷溅等情况，网格法较难精准捕捉到波浪破碎、浪花飞溅等细节。图7展示了FVM和SPH方法模拟高速舰船兴波的结果与Tagliafierro等[84]的模型试验结果的对比。由图可见，FVM只能够模拟出微幅的液面变形，而SPH方法能够很好地捕捉液面的飞溅细节。可见，SPH充分发挥了拉格朗日粒子方法的理论优势，能更准确模拟兴波特征。
早期的计算机内存和效率低，三维仿真计算成本高，故一般采用切片法、二维半[85-86]理论研究航行器的兴波问题。Marrone等[4]通过2D+t SPH方法对细长船体兴波的问题进行研究，对不同弗劳德数下的船艏兴波演化和尾迹进行模拟，较成功地模拟了细长船舶两侧兴波特征，并通过试验对比验证了结果的准确度。但是，2D+t SPH方法的研究对象局限于纵向速度变化小的细长船体，对于横剖面变化大的复杂构型，只有进行三维仿真才可以尽可能全面地保留兴波特征。最近，Mintu等[87]成功实现了实尺度高速舰船船艏破波的三维模拟，验证了三维SPH计算方法的数值精度和技术可行性。
与真实试验结果[84]相比，SPH方法已可以初步模拟船体两侧喷射的水花，如图7所示，但目前仍未能对微小尺度的水气混合多相流实现精准捕捉。高密度比混合多相流模拟是未来SPH方法的发展方向，需选用更精细的粒子分辨率、开发新的理论和数值模型进行求解。Monaghan和Kocharyan[88]首次提出了基于体积分数理论的SPH混合物模型，经过十余年的发展，Fonty等[89-90]提出的SPH混合物模型在模拟振荡水柱波浪能转换器的水−气高速耦合作用方面表现优越，可进一步拓展应用于航行器（体）的兴波模拟中。SPH混合物模型在高速水动力学应用领域发展前景广阔，相信未来会应用于模拟兴波水花及其他大密度比多相流体扩散、混合过程。
2.2 非线性波浪砰击
2.2.1 SPH数值造波与消波
水面航行器高速航行时会受到反复交替的非线性波浪砰击载荷作用，尤其是在恶劣海况下，波浪力所引起的砰击压力和力矩可能会造成海洋结构物的局部毁伤甚至整体倾覆，因此研究波浪与浮体耦合作用意义重大。近年来，数值波浪水池以及波浪与结构物的耦合作用模型迅速发展，其中数值造波与消波技术成为研究重点。得益于SPH方法模拟动边界的天然优势，SPH方法可通过固定虚粒子理论和技术构建数值造波板，对其运动予以控制，模拟物理水池中的推板式[91]、活塞式[92]、摇板式[93]等造波机，生成多种形式的波浪[94]。
SPH数值水池消波技术可分为被动消波和主动消波。被动消波是指通过斜坡和多孔结构[95]或在数值水池中设置人工阻尼区进行消波[92, 96]，而主动消波方法是通过改变数值造波板的运动机制达到消波目的。虚粒子组成的造波板会根据反射波的变化重新调整运动方程，使反射波与新生成的波叠加形成与原波形一致的波浪[91]，从而保证结构物受恒定的数值波浪作用。研究表明，SPH方法可以产生包括不规则波[91]、畸形波[94]、孤立波[92]等各类波形，造波质量较高，为进一步研究浪固耦合问题提供了技术支撑和保障。
2.2.2 甲板上浪与畸形波砰击
若巨幅波浪砰击船体、海洋平台等结构物，一般会造成严重的波浪爬升，甚至可能翻越甲板，发生甲板上浪现象，导致甲板设备严重毁坏或人员伤亡等，因此，受到了研究人员的高度重视[97-98]。早期的SPH方法在研究舰船甲板上浪问题时，为降低计算难度，通常是通过二维仿真波浪冲击翻越固定水平平板[10]过程来进行研究。而随着计算机计算能力的提高，现已能够对舰船航行的上浪情况进行三维模拟，进一步研究甲板上浪对上层建筑的破坏力[99]。为更精确预报砰击载荷，Areu-Rangel等[100]通过对比SPH方法的仿真结果和精密实验仪器的测量结果，优化了甲板上浪的SPH数值模型，该方法用于预报甲板上浪压力载荷的精度得以验证，有效性和可行性也得到证明。
传统的规则波和不规则波理论难以解释深海中时常出现的极大波高，因此，近年来兴起了对极端海况下畸形波和畸形波砰击海洋结构物的研究。Sun等[94]基于规则波和畸形波理论，采用推板和摇板式造波数值技术联合人工阻尼消波技术，建立了数值波浪水池的SPH数值模型，以研究规则波、聚焦波与结构物的浪固耦合作用，结果如图8（a）所示。针对Zhao等[101-102]提出的畸形波−结构物耦合运动算例，SPH方法可预报浮体结构物的纵荡、升沉、纵摇运动和波浪砰击、甲板上浪、回流等现象，计算结果与试验结果吻合，如图8（b）所示。
![]()
图 8 SPH数值波浪水槽模拟的非线性波浪砰击固定或浮动结构物的结果对比Figure 8. The results comparison of nonlinear wave slamming on a fixed or floating structure simulated in a SPH numerical wave flume畸形波砰击过程中会卷入气体，波浪翻卷上涌甲板后，受气相的影响出现负压区，如图8（a）所示。Sun等[94]通过研究砰击过程中的负压现象，指出一次砰击过程相当于进水与出水过程的耦合，非线性波浪砰击退去后，会在结构下方（例如外漂底部）产生负压，而负压在SPH方法中会带来张力不稳定性，随之造成非物理性的流场空洞并导致流场演化的错误。文献[94]模拟结果还表明，当波浪砰击甲板边缘时，由于砰击速度高，卷入的气穴会形成负压（相对于背景压力）而导致流体吸附。此时，流体并不会立即在甲板上分离，而是在甲板表面形成高速吸附流，这就要求SPH模拟能精确地预报流场中负压形成的吸附力。对于此问题的研究，研究人员建议使用SPH张力不稳定性控制技术[44]。此外，波浪翻越甲板的过程还需考虑空气的气垫效应[94]，否则容易导致压力峰值预报失真。总之，涉及甲板上浪的浪固耦合问题还需进一步完善SPH的理论和方法，建立多相流SPH模型[17]，在考虑空气影响的情况下进行数值模拟研究。
3. 航行体跨介质水动力问题
航行体跨介质过程是指物体出水和入水，实质上也是一个复杂的多相流−固耦合过程。流体与结构物的相互强耦合可能导致相变、湍流和空化，力学机理极具复杂性和挑战性。目前，对出水和入水力学机制的研究方法主要采用试验方法[103]、数值模拟[51]或两者结合的方法。研究表明，SPH方法能很好地模拟此类大变形、多边界和多相流问题[15]。
3.1 细长体入水
细长航行体入水是典型的瞬态强非线性动力学过程，入水瞬间的砰击作用会造成强烈的液面变形，形成液滴喷溅。面对此类问题，网格法受网格尺度限制，对喷溅的模拟略显逊色。图9给出了采用SPH方法、VOF方法计算模拟细长圆柱体（细长体）以100 m/s高速入水的结果对比。由图9可见，网格法（VOF）难以捕捉到喷溅细节，多相界面相对模糊，而SPH方法在流场喷溅特性的捕捉方面表现更佳。图10所示为该算例中运用不同算法预报的细长体端部砰击压力和运动速度曲线。由图10可见，SPH方法能够精确地捕捉到瞬态冲击载荷的峰值，获得的细长体运动速度与CEL方法更吻合。可见，SPH方法能够精确地对航行体高速入水冲击进行仿真，尤其是液面喷溅模拟方面的优势更明显。
![]()
![]()
图 10 细长体高速入水砰击压力与运动速度变化曲线Figure 10. Time evolution of impact pressure and velocity of the slender body during high-speed water entry高速入水问题主要关注细长体结构局部砰击区域所受载荷及其附近流场的演化过程，而远场流动变化随着距离的增大而减小。因此，为了在保证局部高精度的同时提高计算效率，Sun等[44]采用自适应粒子细化技术（adaptive particle refinement, APR）对大范围的计算域分设多级粒子分辨率。该技术也能根据需求定义高分辨率区域，通过此区域动态跟踪细长体结构运动的过程，并可对整个弹体周围流场区域进行加密，精准预报流体对弹体和弹道的影响，如图11（a）所示。此外，APR技术也可仅对弹体头部进行局部加密，捕捉弹头区域的流动特征，如图11（b）所示（
\Delta x 表示粒子间距）。总之，APR技术为SPH方法实现高效精准的仿真提供了技术支撑。![]()
图 11 多级粒子分辨率SPH技术模拟的细长体高速入水过程Figure 11. High-speed water entry process of a slender body simulated by SPH with APR technique前人基于SPH方法的许多入水问题的研究，例如旋转[104]、倾斜[105]入水的仿真以及空腔演化特征等，大部分忽略了空腔闭合后的内部气体对结构运动的影响。首先，这是因为空腔闭合后会产生高速射流[17]，冲击结构物表面并造成运动姿态变化，所以空腔的产生及气相的影响对结构载荷与运动预报有着重要意义[103, 106]，需要采用多相流SPH模型开展计算，详见文献[17]。其次，砰击入水的高速运动会导致细长体周边产生空化，且目前SPH理论框架内尚未建立完备的空化理论和数值模型，如何做到空化、湍流[107]、多相SPH模型的结合以实现精准数值预报仍有待深入研究。
3.2 细长体出水
SPH方法为细长体高速入水过程的模拟提供了可靠数值方案，对于细长体出水过程其同样具有较精确的预报能力。此外，高速出水过程还涉及复杂气−液−固三相的耦合，包括瞬态强冲击载荷、空泡产生及演化和流−固耦合效应等，这也是工程前沿所要研究的重要课题。为此，前人开展了丰富的数值和试验研究，包括球体出水[109]和圆柱出水仿真并结合试验校核[110]等。
在细长体高速出水时，其肩部或底部会出现相对背景压力的负压现象，负压在SPH数值计算中会导致强烈的张力不稳定。通过建立张力不稳定性控制理论（tensile instability control, TIC）可避免细长体出水过程的非物理性数值空洞[5]，而且，还可通过多级粒子分辨率技术对细长体附近区域的粒子进行加密，提高局部区域的精度。 图12给出了细长体高速出水过程的初步模拟结果。由图可见，对于高速出水问题研究，SPH方法已具备较强的预报能力。
![]()
图 12 SPH方法模拟的细长体高速出水过程Figure 12. Numerical simulation of high-speed water exit process of a slender body by SPH method细长体从空中入水的瞬态过程中砰击载荷占主导地位，计算过程一般忽略黏性力，但因出水过程涉及了空化、湍流、强可压过程，通常受黏性严重影响，所以出水与入水并非是完全逆向过程[8]。Zhang和Sun等[8]采用δ+-SPH方法研究二维圆柱体出水过程，使用TIC技术成功模拟了圆柱体底部产生的涡旋分离，所得结果比边界元法（BEM）更精准。
高速出水问题还需要考虑细长体出水过程肩部产生的空泡，这就需要开发SPH理论框架下的空化模型，精确预报空泡的产生、演化和溃灭过程。空化问题具有强可压特性，Sun等[111]提出的体积自适应粒子撕裂与融合理论和技术在应对强可压的问题时具有较强的适用性，能够为开发SPH空化模型提供基础支撑。然而，目前传统的计算流体力学（CFD）算法模拟空化相变的相关技术[112]暂时难以直接拓展应用到SPH算法中，亟需在未来研究中重点开展此项工作。
4. 水下爆炸与结构毁伤
水下爆炸是一个涉及高温高压爆炸产物剧烈膨胀的强非线性过程[19]，爆炸过程分别与船体结构和海况相关，研究极具挑战性，难以通过单纯的理论和试验方法开展研究，而数值模拟是实现实尺度预报的最佳策略之一。
从目前来看，远场水下爆炸载荷的预报理论相对完善，但近场和超近场水下爆炸载荷预报仍十分困难。SPH方法模拟水下爆炸问题时，可自动捕捉多相界面，模拟从起爆、冲击波传播到气泡膨胀的全过程。当SPH算法与结构求解器进行耦合时，可计算船体从损毁到沉没的全过程[6, 113]。本节将对SPH理论和方法在研究水下爆炸冲击波和气泡脉动方面取得的进展进行综述。
4.1 水下爆炸冲击波模拟
炸药在水下引爆后会产生高温高压的爆炸产物，辐射的高热量使附近的水瞬时汽化，形成高温高压气泡，并向外辐射形成冲击波。水下爆炸中冲击波的威力占据了总能量的一半左右。爆炸后产生的瞬态冲击波在多相中的传播，具有强可压、强非线性等特征，这对SPH算法的精确性和稳定性要求极高。而以往的SPH理论和方法基于不可压缩[59]或弱可压假设[49]，难以直接应用于水下爆炸这类强压缩性问题，尤其是对水下爆炸气泡的周期性膨胀和收缩过程难以精准模拟。
Riemann SPH方法的出现推动了粒子方法处理可压缩问题的应用发展，但早期在捕捉激波时的精度不如成熟的网格法，在理论方面还需进一步提高。因此，基于传统SPH理论，借鉴和引入网格法中处理可压缩流动的先进数值技术及高精度计算框架，Meng和Zhang等[75]提出的TENO-SPH模型与方法，在冲击波捕捉和分辨方面具备了较高的数值精度和计算能力，增强了Riemann SPH方法处理此类问题的鲁棒性。Sun等[111]针对强可压问题的数值特征，提出一种新型的粒子体积自适应理论，实现了粒子在膨胀作用下撕裂和收缩时的融合模拟，较准确地预报了冲击波载荷。但是，对于气体膨胀压缩导致的核函数影响域内粒子数的变化问题，通常还需采用变光滑长度技术[114]，来提高SPH方法的计算精度和稳定性。
在水下爆炸的具体计算中，SPH相关处理技术和方法取得了可观的进展。Wang和Zhang等[58]提出基于特征线原理的无反射边界条件，有效消除了水下爆炸冲击波计算中的边界反射，为SPH方法用于高精度模拟水下爆炸提供了依据。彭玉祥[115]采用SPH方法模拟文献[116]中相同工况下的二维近平面固壁柱状水下爆炸算例，研究了高压气泡产生的冲击波和稀疏波的传播，求解的压力结果与参考结果高度吻合，为SPH方法用于模拟强可压瞬态流动的可行性和有效性提供了参考。同时，文献[115]针对三维自由场的水下爆炸问题进行模拟，将计算得到的冲击波压力时历曲线与经验公式进行了对比，两者吻合较好，体现了SPH方法预报冲击波压力的良好精度。
在计算三维轴对称水下爆炸问题时，还可以通过轴对称SPH数值模型[117-119]进行模拟，以减小计算量。图13给出了采用轴对称SPH方法计算得到的水下爆炸几个典型时刻的冲击波压力云图。轴对称SPH方法的计算量小，相对于直接三维模拟，可采用更加精细的粒子分辨率，因而计算得到的冲击波波阵面十分锐利。由图可见，SPH方法模拟水下爆炸冲击波阶段已发展得相当成熟可靠，具备了水下爆炸冲击波阶段载荷的精确预报能力。
![]()
图 13 轴对称SPH方法模拟的水下爆炸几个典型时刻的冲击波压力云图Figure 13. Pressure contours of the shock wave induced by underwater explosion at typical time instant by axisymmetric SPH model4.2 水下爆炸气泡模拟
May和Monaghan[120]最早采用SPH方法研究了气泡引起的舰船沉没过程。在此研究领域，文献[10]主要考虑的是巨大的上浮气泡，而事实上更不可忽视的是水下爆炸气泡及其在舰船附近脉动激起的鞭状运动和射流对结构的冲击效应。研究水下爆炸产生的大尺度脉动气泡，需考虑环境中的静水压力、大气压力、重力及边界等的耦合作用，以及气泡脉动产生的热交换和能量耗散，此机理十分复杂。在上述方面，前人提出了理论、试验和计算等多种方法进行研究，取得了丰硕成果[7, 121]。
SPH方法尽管在处理大变形和动边界问题时具有明显优势，但用于模拟水下爆炸气泡脉动较为少见，其主要原因是，爆炸气泡涉及了爆炸气体的强压缩和膨胀过程，给粒子法模拟带来了挑战。Joshi等[122]对固体边界的空泡崩塌进行了模拟，然而忽略了气体粒子以及气泡的膨胀过程；Pineda等[123]也进行了多相模型模拟空泡崩塌，但因缺乏粒子体积自适应技术，气体粒子体积被过度压缩，导致水−气界面出现了明显的锯齿状。总之，水下爆炸气泡SPH模拟的难点主要体现在气泡脉动过程中。SPH理论的拉格朗日粒子特性决定了气体粒子分布会随气泡体积大幅度变化。为简化问题的复杂性，目前，SPH方法暂未计入气泡脉动过程中的热力学效应和能量损失，首要任务是需要提出、验证和优化适用于强可压问题的SPH理论，以增强SPH方法模拟气泡脉动的可行性，提高对气泡脉动和射流的仿真精度。
采用SPH方法计算爆炸气泡时，粒子不仅会因气泡膨胀变得十分稀疏，也会因气泡收缩而变得十分稠密，使得计算的载荷结果不准确[111]。如图14所示，当气泡体积收缩至最小时（见图14左侧），气体粒子严重集聚，核函数半径范围内粒子数量急剧增多；相反，当气泡体积膨胀到最大时，气泡粒子的间距随之增大，核函数半径范围内粒子数量急剧减少（见图14右侧）。以上气泡收缩和膨胀过程中，核函数内部粒子数量大幅变化，但气泡外围的水粒子间距几乎不变（水的压缩性较小所导致）。由此，造成水−气界面的两侧粒子分布极不均衡，使得水−气界面不光顺，计算精度剧烈下降甚至计算中断。为解决SPH方法模拟空泡脉动时气体粒子的体积和间距剧烈变化所带来的计算精度及稳定性问题，Sun等[111]建立了基于SPH体积自适应理论（volume adaptive scheme, VAS）的粒子撕裂−融合技术，成功模拟了水下爆炸气泡在自由场、自由液面、壁面等边界下的脉动过程。
![]()
图 14 气泡脉动时气体粒子体积和间距变化示意图Figure 14. Variation of the volume and spacing of gas particles during the pulsation of a bubble尽管SPH理论和方法拥有精确捕捉大变形水−气界面的优势，但在处理三维气泡脉动问题时，因需要较大的计算域以避免边界影响而使得计算量较大、效率较低。为此，Sun等[117]构建了轴对称强可压多相流SPH模型，实现了SPH方法对水下爆炸气泡脉动的模拟，可精确捕捉高压气泡的膨胀、收缩、崩塌、射流等过程。图15给出了自由场溃灭气泡半径演化和自由液面附近气泡膨胀及收缩时最大宽度演化的SPH模拟结果与参考数据[124-126]的对比验证[117]。由图可见，轴对称SPH方法能准确预报不同条件下气泡的膨胀和收缩动态过程。
![]()
本文采用Sun等[117]的轴对称SPH方法，模拟了Tian等[127]给出的自由液面以下10 m处500 kg装药所产生的水下爆炸气泡脉动和射流过程，如图16所示。结果表明，计算得到的气泡膨胀和射流过程与Tian等[127]提供的数值结果十分吻合。从数值模拟结果可以看出，基于Sun 等[111]提出的VAS理论，采用粒子撕裂−融合技术，SPH算法可用于模拟水下爆炸冲击波和气泡脉动的全过程。最近，Fang等[119]将VAS理论与Riemann SPH方法结合应用于激波及入水问题，也取得了较好的计算精度，验证了SPH理论和方法应用于水下爆炸及气泡动力学的可行性及有效性，为进一步深入研究水下爆炸力学和载荷机理提供了更多元的求解方案。
![]()
图 16 自由液面附近水下爆炸气泡脉动和射流的SPH模拟Figure 16. SPH simulations of bubble pulsation and jetting near a free surface4.3 水下爆炸结构毁伤模拟
如上所述，SPH方法因其不依赖网格，极为适合用于模拟大变形流−固耦合问题。早在1991年，Libersky等[128]就将SPH方法应用到了固体结构的冲击碰撞断裂的研究中，将SPH方法的应用领域拓宽到了固体力学领域。早期运用SPH方法研究固体断裂时都采用三维实体对结构进行建模，但考虑到汽车、飞机和舰船等工程结构中广泛采用的是薄壳结构，采用三维实体建模会导致壳体厚度方向的粒子间距极小，从而限制时间积分的增量，使得计算效率降低。在2008年，Maurel等[129]提出了SPH壳单元理论，解决了时间增量受壳体厚度限制的缺点，极大提高了SPH方法在薄壳结构动响应方面的求解能力。此后，Caleyron等[130]又将该理论应用到了对薄壳结构冲击断裂响应的模拟中。同时，Ming等[131]应用并发展了该理论，将该理论命名为光滑粒子壳单元（smoothed particle shell，SPS），并应用到了水下爆炸结构毁伤的模拟中[132]。
然而，因SPH理论和方法采用的是强形式的控制方程，经过使用移动最小二乘法（moving least squares， MLS）形函数修正其核函数后，使之不能自动满足结构自由边界条件，需要人工施加自由边界条件[133-134]，增加了断裂自由边模拟的复杂度。针对此问题，Peng等[135-136]采用重构核粒子方法（reproducing kernel particle method，RKPM）建立了任意曲壳曲梁三维无网格法的计算模型，实现了加筋壳结构的无网格模拟。而且，在上述基础上，建立了水下爆炸结构毁伤的流−固耦合计算模型[113]，分别采用SPH和RKPM方法求解水下爆炸载荷和舰船结构的断裂响应，并与试验结果进行对比，验证了所提计算模型的有效性和计算精度。图17给出了水下爆炸时舰船结构断裂毁伤的SPH-RKPM数值仿真结果。由图可见，该数值计算模型具备了预报水下爆炸时的舰船毁伤能力。目前，张阿漫教授团队建立了SPH-RKPM流−固耦合动力学模型及计算方法，开发了具有自主知识产权的水下爆炸舰船毁伤数值计算FSLAB软件[6]，该软件被应用到了舰船结构强冲击毁伤的模拟之中，广泛论证了SPH-RKPM耦合计算方法在水下爆炸领域的应用前景，能够为舰船防护结构设计提供理论依据和基础性技术支撑。
![]()
图 17 SPH-RKPM算法模拟水下爆炸引起的舰船结构毁伤过程Figure 17. Numerical simulations of structural damage resulted from underwater explosion simulated by SPH-RKPM method4.4 破舱涌流与结构动态沉没模拟
SPH理论和方法除了能够精确预报船体在冲击载荷作用下的结构破损外，对破舱涌流和结构沉没的模拟也具有强适用性。在船体结构破损情况下，涌流灌入破口后与波浪的相互耦合作用，会使船体产生剧烈的横摇、升沉等多自由度的复杂运动。Guo等[137]采用三维SPH方法对静水中不同破口位置的破舱动态沉没过程进行了仿真，通过相关试验验证了SPH方法的精度和稳定性，为破舱动态沉没问题提供了基准算例，其舷侧破口涌流的仿真结果与试验结果对比如图18（a）所示。 Cheng等[138] 、Ming等[139]和Cao等[140]构造了SPH数值水池，对多水密舱体在波浪耦合作用下的沉没过程进行研究，准确模拟了舱内涌流晃动和外部波浪的耦合过程，进一步完善了破损结构在波浪环境下的动态沉没力学机理，如图18（b）所示的沉没过程[138]。综上，建议未来考虑舱内气体的真实压缩性，基于VAS框架的多级粒子分辨率技术和多相流模型[141]，进一步开发适用于破舱涌流的高精度SPH理论和方法，以提高模拟精度和稳定性。SPH方法用于水下爆炸的各环节及船体破口与动态沉没过程均具有较强的数值模拟能力，预期未来能够实现将SPH方法应用到水下爆炸全过程的精准仿真。
![]()
图 18 三维SPH方法模拟破损舱段涌流和沉没过程的结果与试验结果对比Figure 18. Comparison between experimental and 3D SPH simulation results of flowing and sinking process due to a damaged ship cabin5. 高速水动力学耦合算法
考虑到SPH数值模拟在实际工程应用中难以规避计算成本的问题，为充分发挥SPH模拟大变形问题的优势，提高其在船海力学领域的应用范围，建议SPH方法在未来发展上应重视与其他算法的耦合。例如，开发有/无网格耦合算法、黏流−势流耦合算法等，构建如图19所示的耦合计算框架，以解决船海高速水动力领域常见的出水和入水以及水下爆炸与冲击问题。图19所示的耦合算法可在流−固耦合作用剧烈的区域采用SPH粒子法进行局部范围的精准计算，在较小变形的外围区域使用黏流网格法进行高效求解，在远场区域可采用势流方法进行大范围海域的模拟。事实上，文献[142]中的部分耦合算法已为该框架的搭建和实现奠定了坚实的技术基础，例如，SPH-FVM算法[143]在大变形流动仿真上拥有较好的稳定性，已拓展应用至航行体的兴波、高速入水等问题。此外，高阶谱（higher-order spectral, HOS）方法与网格法求解器的耦合也得到了验证[144]，其适合用于对大范围海域内的船海水动力问题进行黏流−势流耦合计算。图19所示的多算法耦合计算框架通过结合有网格、无网格和黏流、势流数值算法的优点进行耦合求解，有望为SPH理论和方法应用于实际船海工程问题提供新的技术方案，为实现高精度、高效率的船海工程应用仿真奠定基础。
![]()
图 19 有/无网格耦合算法和黏流−势流耦合算法求解典型高速水动力问题示意图Figure 19. Schematics of coupled algorithm between mesh-based and particle-based methods and between viscous-flow and potential-flow solvers for typical high-speed hydrodynamic problems6. 结 语
本文综述了SPH理论与方法在船海高速水动力学研究中的最新进展。可见，SPH理论和方法日趋得到完善，相关数值方法在高速舰船兴波、细长体出水和入水、水下爆炸与冲击等高速水动力问题中已得到广泛应用，取得了较高的计算精度，在精确捕捉大变形的多相界面和流−固界面等方面具备明显优势。
在未来研究中，SPH理论与方法在以下几个方面仍有提高的空间，主要包括：
1） 在计算精度和效率方面，进一步提高SPH理论和方法的完备性及数值格式的收敛阶数，实现以较少粒子数量达到预期的计算精度，提高计算效率。
2） 在边界处理方面，仍需进一步发展三维复杂构型壁面边界的SPH数值处理技术，减弱边界效应对物理问题模拟结果的影响。
3） 在应用范围和领域方面，开发SPH理论框架下的湍流模型和空化模型，加强高雷诺数流动和相变问题的模拟能力。同时，发展基于体积分数的SPH水气混合物的理论和数值模型，进一步拓展应用于高速航行体的兴波和水汽泡混合流模拟中。
4） 在解决实际工程问题方面，进一步提高SPH方法和计算程序的高性能并行计算能力，与国产大型超级计算机的能力结合，实现亿级粒子数的大规模并行化模拟，增强SPH理论和方法的工程化应用能力。
7. 致 谢
感谢哈尔滨工程大学明付仁副教授、王平平博士和中国海洋大学程晗博士对本文水下爆炸冲击波和细长体出入水计算提供的帮助。
-
![]()
图 1 三维圆柱体和二维楔形体入水数值模拟结果
Figure 1. Numerical simulations of water entry of a 2D wedge and a 3D cylinder
![]()
图 5 复杂构型结构物的CAD建模和粒子化离散
Figure 5. CAD modeling and particle discretization of a complex structure
![]()
图 6 三维SPH方法模拟的“中山大学”号科考船高速航行兴波和飞机水上迫降
Figure 6. 3D SPH simulations of the breaking wave of SYSU research vessel in high-speed and the aircraft ditching process
![]()
图 8 SPH数值波浪水槽模拟的非线性波浪砰击固定或浮动结构物的结果对比
Figure 8. The results comparison of nonlinear wave slamming on a fixed or floating structure simulated in a SPH numerical wave flume
![]()
![]()
图 10 细长体高速入水砰击压力与运动速度变化曲线
Figure 10. Time evolution of impact pressure and velocity of the slender body during high-speed water entry
![]()
图 11 多级粒子分辨率SPH技术模拟的细长体高速入水过程
Figure 11. High-speed water entry process of a slender body simulated by SPH with APR technique
![]()
图 12 SPH方法模拟的细长体高速出水过程
Figure 12. Numerical simulation of high-speed water exit process of a slender body by SPH method
![]()
图 13 轴对称SPH方法模拟的水下爆炸几个典型时刻的冲击波压力云图
Figure 13. Pressure contours of the shock wave induced by underwater explosion at typical time instant by axisymmetric SPH model
![]()
图 14 气泡脉动时气体粒子体积和间距变化示意图
Figure 14. Variation of the volume and spacing of gas particles during the pulsation of a bubble
![]()
![]()
图 16 自由液面附近水下爆炸气泡脉动和射流的SPH模拟
Figure 16. SPH simulations of bubble pulsation and jetting near a free surface
![]()
图 17 SPH-RKPM算法模拟水下爆炸引起的舰船结构毁伤过程
Figure 17. Numerical simulations of structural damage resulted from underwater explosion simulated by SPH-RKPM method
![]()
图 18 三维SPH方法模拟破损舱段涌流和沉没过程的结果与试验结果对比
Figure 18. Comparison between experimental and 3D SPH simulation results of flowing and sinking process due to a damaged ship cabin
-
[1] ZHANG Z R, LIU H, ZHU S P, et al. Application of CFD in ship engineering design practice and ship hydrodynamics[J]. Journal of Hydrodynamics, Ser. B, 2006, 18(Supp 3): 315–322.
[2] 王建华, 万德成. CFD数值模拟船舶在波浪中的回转操纵运动[J]. 中国舰船研究, 2019, 14(1): 1–8. WANG J H, WAN D C. CFD simulation of ship turning motion in waves[J]. Chinese Journal of Ship Research, 2019, 14(1): 1–8 (in Chinese).
[3] 刘鑫旺, 万德成. 豪华邮轮多航速兴波阻力的船型优化[J]. 中国舰船研究, 2020, 15(5): 1–10,40. LIU X W, WAN D C. Hull form optimization of wave-making resistance in different speeds for a luxury cruise ship[J]. Chinese Journal of Ship Research, 2020, 15(5): 1–10,40 (in Chinese).
[4] MARRONE S, COLAGROSSI A, ANTUONO M, et al. A 2D+t SPH model to study the breaking wave pattern generated by fast ships[J]. Journal of Fluids and Structures, 2011, 27(8): 1199–1215. doi: 10.1016/j.jfluidstructs.2011.08.003
[5] LYU H G, SUN P N, HUANG X T, et al. On removing the numerical instability induced by negative pressures in SPH simulations of typical fluid-structure interaction problems in ocean engineering[J]. Applied Ocean Research, 2021, 117: 102938. doi: 10.1016/j.apor.2021.102938
[6] 彭玉祥, 张阿漫, 薛冰, 等. 强冲击作用下舰船结构毁伤的三维无网格SPH-RKPM方法数值模拟[J]. 中国科学: 物理学、力学、天文学, 2021, 51(12): 124614. PENG Y X, ZHANG A M, XUE B, et al. Numerical investigation of ship structure damage subject to strong impact using a 3D meshless SPH-RKPM method[J]. Scientia Sinica:Physica, Mechanica & Astronomica, 2021, 51(12): 124614 (in Chinese).
[7] 张阿漫, 王诗平, 彭玉祥, 等. 水下爆炸与舰船毁伤研究进展[J]. 中国舰船研究, 2019, 14(3): 1–13. ZHANG A M, WANG S P, PENG Y X, et al. Research progress in underwater explosion and its damage to ship structures[J]. Chinese Journal of Ship Research, 2019, 14(3): 1–13 (in Chinese).
[8] ZHANG A M, SUN P N, MING F R, et al. Smoothed particle hydrodynamics and its applications in fluid-structure interactions[J]. Journal of Hydrodynamics, Ser. B, 2017, 29(2): 187–216. doi: 10.1016/S1001-6058(16)60730-8
[9] YE T, PAN D Y, HUANG C, et al. Smoothed particle hydrodynamics (SPH) for complex fluid flows: Recent developments in methodology and applications[J]. Physics of Fluids, 2019, 31(1): 011301. doi: 10.1063/1.5068697
[10] GÓMEZ-GESTEIRA M, CERQUEIRO D, CRESPO C, et al. Green water overtopping analyzed with a SPH model[J]. Ocean Engineering, 2005, 32(2): 223–238. doi: 10.1016/j.oceaneng.2004.08.003
[11] 于汉, 李清, 杨德庆. 水面舰船粘性流场和流噪声的数值计算[J]. 中国舰船研究, 2017, 12(6): 22–29. doi: 10.3969/j.issn.1673-3185.2017.06.004 YU H, LI Q, YANG D Q. Numerical simulation of viscous flow and hydrodynamic noise in surface ship[J]. Chinese Journal of Ship Research, 2017, 12(6): 22–29 (in Chinese). doi: 10.3969/j.issn.1673-3185.2017.06.004
[12] WANG B L, GUO X Y, LIU H, et al. Numerical simulations of wake signatures around high-speed ships[J]. Journal of Hydrodynamics, Ser. B, 2015, 26(6): 986–989.
[13] REED A M, MILGRAM J H. Ship wakes and their radar images[J]. Annual Review of Fluid Mechanics, 2002, 34(1): 469–502. doi: 10.1146/annurev.fluid.34.090101.190252
[14] CHEN C, ZHANG A M, CHEN J Q, et al. SPH simulations of water entry problems using an improved boundary treatment[J]. Ocean Engineering, 2021, 238: 109679. doi: 10.1016/j.oceaneng.2021.109679
[15] SUN P N, MING F R, ZHANG A M. Numerical simulation of interactions between free surface and rigid body using a robust SPH method[J]. Ocean Engineering, 2015, 98: 32–49. doi: 10.1016/j.oceaneng.2015.01.019
[16] 王永虎, 石秀华. 入水冲击问题研究的现状与进展[J]. 爆炸与冲击, 2008, 28(3): 276–282. doi: 10.3321/j.issn:1001-1455.2008.03.014 WANG Y H, SHI X H. Review on research and development of water-entry impact problem[J]. Explosion and Shock Waves, 2008, 28(3): 276–282 (in Chinese). doi: 10.3321/j.issn:1001-1455.2008.03.014
[17] LYU H G, DENG R, SUN P N, et al. Study on the wedge penetrating fluid interfaces characterized by different density-ratios: Numerical investigations with a multi-phase SPH model[J]. Ocean Engineering, 2021, 237: 109538. doi: 10.1016/j.oceaneng.2021.109538
[18] 张社荣, 孔源, 王高辉. 水下和空中爆炸冲击波传播特性对比分析[J]. 振动与冲击, 2014, 33(13): 148–153. ZHANG S R, KONG Y, WANG G H. Comparative analysis on propagation characteristics of shock wave induced by underwater and air explosions[J]. Journal of Vibration and Shock, 2014, 33(13): 148–153 (in Chinese).
[19] 张阿漫, 王诗平, 汪玉, 等. 水下爆炸对舰船结构损伤特征研究综述[J]. 中国舰船研究, 2011, 6(3): 1–7. doi: 10.3969/j.issn.1673-3185.2011.03.001 ZHANG A M, WANG S P, WANG Y, et al. Advances in the research of characteristics of warship structural damage due to underwater explosion[J]. Chinese Journal of Ship Research, 2011, 6(3): 1–7 (in Chinese). doi: 10.3969/j.issn.1673-3185.2011.03.001
[20] VON KARMAN T H. The impact on seaplane floats during landing[J]. National Advisory Committee for Aeronatics, 1929.
[21] WANG S P, ZHANG A M, LIU Y L, et al. Bubble dynamics and its applications[J]. Journal of Hydrodynamics, 2018, 30(6): 975–991. doi: 10.1007/s42241-018-0141-3
[22] MARRONE S, BOUSCASSE B, COLAGROSSI A, et al. Study of ship wave breaking patterns using 3D parallel SPH simulations[J]. Computers & Fluids, 2012, 69: 54–66.
[23] LANDRINI M, COLAGROSSI A, GRECO M, et al. The fluid mechanics of splashing bow waves on ships: A hybrid BEM-SPH analysis[J]. Ocean Engineering, 2012, 53: 111–127. doi: 10.1016/j.oceaneng.2012.06.027
[24] 孙鹏楠. 物体与自由液面耦合作用的光滑粒子流体动力学方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2018. SUN P N. Study on SPH method for the simulation of object-free surface interactions[D]. Harbin: Harbin Engineering University, 2018 (in Chinese).
[25] LIU M B, LI S M. On the modeling of viscous incompressible flows with smoothed particle hydro-dynamics[J]. Journal of Hydrodynamics, 2016, 28(5): 731–745. doi: 10.1016/S1001-6058(16)60676-5
[26] 陈亚东, 陆凡, 孙华圣, 等. 基于离散单元法的抗拔桩承载特性研究[J]. 水利水电技术, 2020, 51(9): 200–204. CHEN Y D, LU F, SUN H S, et al. Study on bearing behavior of uplift pile based on discrete element method[J]. Water Resources and Hydropower Engineering, 2020, 51(9): 200–204 (in Chinese).
[27] 郑温刚, 王媛, 张云云, 等. 基于SPH方法的阶梯式溢洪道消能特性研究[J]. 水利水电技术, 2020, 51(12): 117–124. ZHENG W G, WANG Y, ZHANG Y Y, et al. SPH method-based study on energy dissipation characteristics of stepped spillway[J]. Water Resources and Hydropower Engineering, 2020, 51(12): 117–124 (in Chinese).
[28] 顾声龙, 吴玉帅, 解宏伟, 等. 基于CSPM方法对二维管嘴出流的数值模拟[J]. 水利水电技术, 2016, 47(9): 39–43. GU S L, WU Y S, XIE H W, et al. CSPM method-based numerical simulation on outflow from 2-D pipe nozzle[J]. Water Resources and Hydropower Engineering, 2016, 47(9): 39–43 (in Chinese).
[29] 马理强, 刘谋斌, 常建忠, 等. 液滴冲击液膜问题的光滑粒子动力学模拟[J]. 物理学报, 2012, 61(24): 244701. doi: 10.7498/aps.61.244701 MA L Q, LIU M B, CHANG J Z, et al. Numerical simulation of droplet impact onto liquid films with smoothed particle hydrodynamics[J]. Acta Physica Sinica, 2012, 61(24): 244701 (in Chinese). doi: 10.7498/aps.61.244701
[30] 田鑫, 万德成. MPS方法模拟三维圆柱形液舱晃荡问题[J]. 中国舰船研究, 2019, 14(3): 116–121. TIAN X, WAN D C. Simulation of sloshing in three-dimensional cylindrical tank by MPS method[J]. Chinese Journal of Ship Research, 2019, 14(3): 116–121 (in Chinese).
[31] HASHIMOTO H, GRENIER N, SUEYOSHI M, et al. Comparison of MPS and SPH methods for solving forced motion ship flooding problems[J]. Applied Ocean Research, 2022, 118: 103001. doi: 10.1016/j.apor.2021.103001
[32] ABDELRAZEK A M, KIMURA I, SHMIZU Y. Comparison between SPH and MPS methods for numerical simulations of free surface flow problems[J]. Journal of Japan Society of Civil Engineers, Ser. B1 (Hydraulic Engineering), 2014, 70(4): I_67–I_72. doi: 10.2208/jscejhe.70.I_67
[33] BAKTI F P, KIM M H, KIM K S, et al. Comparative study of standard WC-SPH and MPS solvers for free surface academic problems[J]. International Journal of Offshore and Polar Engineering, 2016, 26(3): 235–243. doi: 10.17736/ijope.2016.pf17
[34] ZHANG Y X, WAN D C. Comparison investigations of numerical simulations of incompressible viscous flows by SPH and MPS[C]//ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai, China: ASME, 2010: 837-845.
[35] 陈翔, 万德成. MPS与GPU结合数值模拟LNG液舱晃荡[J]. 力学学报, 2019, 51(3): 714–729. doi: 10.6052/0459-1879-18-410 CHEN X, WAN D C. Numerical simulation of liquid sloshing in LNG tank using GPU-accelerated MPS method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(3): 714–729 (in Chinese). doi: 10.6052/0459-1879-18-410
[36] 陈翔, 张友林, 万德成. MPS方法研究进展及其在船舶水动力学问题中的应用[J]. 哈尔滨工程大学学报, 2018, 39(6): 955–972. CHEN X, ZHANG Y L, WAN D C. Developments of the MPS method and its applications on hydrodynamics problems[J]. Journal of Harbin Engineering University, 2018, 39(6): 955–972 (in Chinese).
[37] 徐泳, 孙其诚, 张凌, 等. 颗粒离散元法研究进展[J]. 力学进展, 2003, 33(2): 251–260. doi: 10.3321/j.issn:1000-0992.2003.02.010 XU Y, SUN Q C, ZHANG L, et al. Advances in discrete element methods for particulate materials[J]. Advances in Mechanics, 2003, 33(2): 251–260 (in Chinese). doi: 10.3321/j.issn:1000-0992.2003.02.010
[38] SUN X S, SAKAI M, YAMADA Y. Three-dimensional simulation of a solid-liquid flow by the DEM-SPH method[J]. Journal of Computational Physics, 2013, 248: 147–176. doi: 10.1016/j.jcp.2013.04.019
[39] ROBB D M, GASKIN S J, MARONGIU J C. SPH-DEM model for free-surface flows containing solids applied to river ice jams[J]. Journal of Hydraulic Research, 2016, 54(1): 27–40. doi: 10.1080/00221686.2015.1131203
[40] KLOSS C, GONIVA C, HAGER A, et al. Models, algorithms and validation for open source DEM and CFD-DEM[J]. Progress in Computational Fluid Dynamics, 2012, 12(2/3): 140–152.
[41] 王哲, 邓迪, 万德成. 基于CFD方法的变张力柔性圆柱涡激振动数值模拟[J]. 水动力学研究与进展(A辑), 2019, 34(2): 201–209. WANG Z, DENG D, WAN D C. Numerical simulations of vortex-induced vibrations of flexible cylinder with varying tensions based on CFD method[J]. Journal of Hydrodynamics (Ser. A), 2019, 34(2): 201–209 (in Chinese).
[42] 余安正, 万德成. 高航速下KCS模型艏波破碎与艏部涡量数值研究[J]. 水动力学研究与进展(A辑), 2020, 35(1): 122–132. YU A Z, WAN D C. Numerical study of bow wave breaking and vorticity of KCS under high speeds[J]. Journal of Hydrodynamics (Ser. A), 2020, 35(1): 122–132 (in Chinese).
[43] COLAGROSSI A, LANDRINI M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics[J]. Journal of Computational Physics, 2003, 191(2): 448–475. doi: 10.1016/S0021-9991(03)00324-3
[44] SUN P N, COLAGROSSI A, MARRONE S, et al. Multi-resolution Delta-plus-SPH with tensile instability control: Towards high Reynolds number flows[J]. Computer Physics Communications, 2018, 224: 63–80. doi: 10.1016/j.cpc.2017.11.016
[45] CRESPO A C, DOMINGUEZ J M, BARREIRO A, et al. GPUs, a new tool of acceleration in CFD: efficiency and reliability on smoothed particle hydrodynamics methods[J]. PLoS One, 2011, 6(6): e20685. doi: 10.1371/journal.pone.0020685
[46] ZHANG Z F, WANG C, ZHANG A M, et al. SPH-BEM simulation of underwater explosion and bubble dynamics near rigid wall[J]. Science China Technological Sciences, 2019, 62(7): 1082–1093. doi: 10.1007/s11431-018-9420-2
[47] GROENENBOOM P, CARTWRIGHT B, MCGUCKIN D. Recent features and industrial applications of the hybrid SPH-FE method[J]. International Journal of Computational Fluid Dynamics, 2021, 35(1/2): 106–128.
[48] GINGOLD R A, MONAGHAN J J. Smoothed particle hydrodynamics: theory and application to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society, 1977, 181(3): 375–389. doi: 10.1093/mnras/181.3.375
[49] MONAGHAN J J. Simulating free surface flows with SPH[J]. Journal of Computational Physics, 1994, 110(2): 399–406. doi: 10.1006/jcph.1994.1034
[50] NGUYEN V T, VU D T, PARK W G, et al. Navier-Stokes solver for water entry bodies with moving Chimera grid method in 6DOF motions[J]. Computers & Fluids, 2016, 140: 19–38.
[51] SUN P N, ZHANG A M, MARRONE S, et al. An accurate and efficient SPH modeling of the water entry of circular cylinders[J]. Applied Ocean Research, 2018, 72: 60–75. doi: 10.1016/j.apor.2018.01.004
[52] CHENG H, MING F R, SUN P N, et al. Towards the modeling of the ditching of a ground-effect wing ship within the framework of the SPH method[J]. Applied Ocean Research, 2019, 82: 370–384. doi: 10.1016/j.apor.2018.09.014
[53] LUO M, KHAYYER A, LIN P Z. Particle methods in ocean and coastal engineering[J]. Applied Ocean Research, 2021, 114: 102734. doi: 10.1016/j.apor.2021.102734
[54] LIU M B, LIU G R. Smoothed particle hydrodynamics (SPH): an overview and recent developments[J]. Archives of Computational Methods in Engineering, 2010, 17(1): 25–76. doi: 10.1007/s11831-010-9040-7
[55] COLAGROSSI A, ANTUONO M, LE TOUZÉ D. Theoretical considerations on the free-surface role in the smoothed-particle-hydrodynamics model[J]. Physical Review E, 2009, 79(5): 056701. doi: 10.1103/PhysRevE.79.056701
[56] MARRONE S, ANTUONO M, COLAGROSSI A, et al. δ-SPH model for simulating violent impact flows[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(13/14/15/16): 1526–1542.
[57] FEDERICO I, MARRONE S, COLAGROSSI A, et al. Simulating 2D open-channel flows through an SPH model[J]. European Journal of Mechanics-B/Fluids, 2012, 34: 35–46. doi: 10.1016/j.euromechflu.2012.02.002
[58] WANG P P, ZHANG A M, MING F R, et al. A novel non-reflecting boundary condition for fluid dynamics solved by smoothed particle hydrodynamics[J]. Journal of Fluid Mechanics, 2019, 860: 81–114. doi: 10.1017/jfm.2018.852
[59] CUMMINS S J, RUDMAN M. An SPH projection method[J]. Journal of Computational Physics, 1999, 152(2): 584–607. doi: 10.1006/jcph.1999.6246
[60] CHOW A D, ROGERS B D, LIND S J, et al. Incompressible SPH (ISPH) with fast Poisson solver on a GPU[J]. Computer Physics Communications, 2018, 226: 81–103. doi: 10.1016/j.cpc.2018.01.005
[61] CHOW A D, ROGERS B D, LIND S J, et al. Numerical wave basin using incompressible smoothed particle hydrodynamics (ISPH) on a single GPU with vertical cylinder test cases[J]. Computers & Fluids, 2019, 179: 543–562.
[62] CRESPO A J C, DOMÍNGUEZ J M, ROGERS B D, et al. DualSPHysics: open-source parallel CFD solver based on smoothed particle Hydrodynamics (SPH)[J]. Computer Physics Communications, 2015, 187: 204–216. doi: 10.1016/j.cpc.2014.10.004
[63] ZHANG C, REZAVAND M, ZHU Y J, et al. SPHinXsys: an open-source multi-physics and multi-resolution library based on smoothed particle hydrodynamics[J]. Computer Physics Communications, 2021, 267: 108066. doi: 10.1016/j.cpc.2021.108066
[64] VILA J P. On particle weighted methods and smooth particle hydrodynamics[J]. Mathematical Models and Methods in Applied Sciences, 1999, 9(2): 161–209. doi: 10.1142/S0218202599000117
[65] ANTUONO M, COLAGROSSI A, MARRONE S. Numerical diffusive terms in weakly-compressible SPH schemes[J]. Computer Physics Communications, 2012, 183(12): 2570–2580. doi: 10.1016/j.cpc.2012.07.006
[66] ANTUONO M, SUN P N, MARRONE S, et al. The δ-ALE-SPH model: An arbitrary Lagrangian-Eulerian framework for the δ-SPH model with particle shifting technique[J]. Computers & Fluids, 2021, 216: 104806.
[67] NESTOR R M, BASA M, LASTIWKA M, et al. Extension of the finite volume particle method to viscous flow[J]. Journal of Computational Physics, 2009, 228(5): 1733–1749. doi: 10.1016/j.jcp.2008.11.003
[68] LIND S J, XU R, STANSBY P K, et al. Incompressible smoothed particle hydrodynamics for free-surface flows: A generalised diffusion-based algorithm for stability and validations for impulsive flows and propagating waves[J]. Journal of Computational Physics, 2012, 231(4): 1499–1523. doi: 10.1016/j.jcp.2011.10.027
[69] SUN P N, COLAGROSSI A, MARRONE S, et al. The δ-plus-SPH model: Simple procedures for a further improvement of the SPH scheme[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 315: 25–49. doi: 10.1016/j.cma.2016.10.028
[70] SUN P N, COLAGROSSI A, MARRONE S, et al. A consistent approach to particle shifting in the δ-plus-SPH model[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 348: 912–934. doi: 10.1016/j.cma.2019.01.045
[71] ZHANG G M, BATRA R C. Modified smoothed particle hydrodynamics method and its application to transient problems[J]. Computational Mechanics, 2004, 34(2): 137–146.
[72] DILTS G A. Moving-least-squares-particle hydrodynamics—I. Consistency and stability[J]. International Journal for Numerical Methods in Engineering, 1999, 44(8): 1115–1155. doi: 10.1002/(SICI)1097-0207(19990320)44:8<1115::AID-NME547>3.0.CO;2-L
[73] LIU M B, XIE W P, LIU G R. Modeling incompressible flows using a finite particle method[J]. Applied Mathematical Modelling, 2005, 29(12): 1252–1270. doi: 10.1016/j.apm.2005.05.003
[74] WANG P P, ZHANG A M, MENG Z F, et al. A new type of WENO scheme in SPH for compressible flows with discontinuities[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 381: 113770. doi: 10.1016/j.cma.2021.113770
[75] MENG Z F, ZHANG A M, WANG P P, et al. A targeted essentially non-oscillatory (TENO) SPH method and its applications in hydrodynamics[J]. Ocean Engineering, 2022, 243: 110100. doi: 10.1016/j.oceaneng.2021.110100
[76] PURI K, RAMACHANDRAN P. Approximate Riemann solvers for the Godunov SPH (GSPH)[J]. Journal of Computational Physics, 2014, 270: 432–458. doi: 10.1016/j.jcp.2014.03.055
[77] COLAGROSSI A, SOUTO-IGLESIAS A, ANTUONO M, et al. Smoothed-particle-hydrodynamics modeling of dissipation mechanisms in gravity waves[J]. Physical Review E, 2013, 87(2): 023302. doi: 10.1103/PhysRevE.87.023302
[78] ZHU Y J, ZHANG C, YU Y C, et al. A CAD-compatible body-fitted particle generator for arbitrarily complex geometry and its application to wave-structure interaction[J]. Journal of Hydrodynamics, 2021, 33(2): 195–206. doi: 10.1007/s42241-021-0031-y
[79] ADAMI S, HU X Y, ADAMS N A. A generalized wall boundary condition for smoothed particle hydrodynamics[J]. Journal of Computational Physics, 2012, 231(21): 7057–7075. doi: 10.1016/j.jcp.2012.05.005
[80] CHENG H, MING F R, SUN P N, et al. Ship hull slamming analysis with smoothed particle hydrodynamics method[J]. Applied Ocean Research, 2020, 101: 102268. doi: 10.1016/j.apor.2020.102268
[81] DOMÍNGUEZ J M, FOURTAKAS G, ALTOMARE C, et al. DualSPHysics: from fluid dynamics to multiphysics problems[J]. Computational Particle Mechanics, 2021: 1–29.
[82] GAROOSI F, HOOMAN K. Numerical simulation of multiphase flows using an enhanced volume-of-fluid (VOF) method[J]. International Journal of Mechanical Sciences, 2022, 215: 106956. doi: 10.1016/j.ijmecsci.2021.106956
[83] DI MASCIO A, BROGLIA R, MUSCARI R. On the application of the single-phase level set method to naval hydrodynamic flows[J]. Computers & Fluids, 2007, 36(5): 868–886.
[84] TAGLIAFIERRO B, MANCINI S, ROPERO-GIRALDA P, et al. Performance assessment of a planing hull using the smoothed particle hydrodynamics method[J]. Journal of Marine Science and Engineering, 2021, 9(3): 244. doi: 10.3390/jmse9030244
[85] VEEN D, GOURLAY T. A combined strip theory and smoothed particle hydrodynamics approach for estimating slamming loads on a ship in head seas[J]. Ocean Engineering, 2012, 43: 64–71. doi: 10.1016/j.oceaneng.2012.01.026
[86] ANDRILLON Y, ALESSANDRINI B. A 2D+T VOF fully coupled formulation for the calculation of breaking free-surface flow[J]. Journal of Marine Science and Technology, 2004, 8(4): 159–168. doi: 10.1007/s00773-003-0167-1
[87] MINTU S, MOLYNEUX D, COLBOURNE B. Full-scale SPH simulations of ship-wave impact generated sea spray[J]. Ocean Engineering, 2021, 241: 110077. doi: 10.1016/j.oceaneng.2021.110077
[88] MONAGHAN J J, KOCHARYAN A. SPH simulation of multi-phase flow[J]. Computer Physics Communications, 1995, 87(1/2): 225–235.
[89] FONTY T, FERRAND M, LEROY A, et al. Mixture model for two-phase flows with high density ratios: a conservative and realizable SPH formulation[J]. International Journal of Multiphase Flow, 2019, 111: 158–174. doi: 10.1016/j.ijmultiphaseflow.2018.11.007
[90] FONTY T, FERRAND M, LEROY A, et al. Air entrainment modeling in the SPH method: a two-phase mixture formulation with open boundaries[J]. Flow, Turbulence and Combustion, 2020, 105(4): 1149–1195. doi: 10.1007/s10494-020-00165-7
[91] ALTOMARE C, DOMÍNGUEZ J M, CRESPO A J C, et al. Long-crested wave generation and absorption for SPH-based DualSPHysics model[J]. Coastal Engineering, 2017, 127: 37–54. doi: 10.1016/j.coastaleng.2017.06.004
[92] HE M, KHAYYER A, GAO X F, et al. Theoretical method for generating solitary waves using plunger-type wavemakers and its smoothed particle hydrodynamics validation[J]. Applied Ocean Research, 2021, 106: 102414. doi: 10.1016/j.apor.2020.102414
[93] ANTUONO M, COLAGROSSI A, MARRONE S, et al. Propagation of gravity waves through an SPH scheme with numerical diffusive terms[J]. Computer Physics Communications, 2011, 182(4): 866–877. doi: 10.1016/j.cpc.2010.12.012
[94] SUN P N, LUO M, LE TOUZÉ D, et al. The suction effect during freak wave slamming on a fixed platform deck: smoothed particle hydrodynamics simulation and experimental study[J]. Physics of Fluids, 2019, 31(11): 117108. doi: 10.1063/1.5124613
[95] REN B, WEN H J, DONG P, et al. Numerical simulation of wave interaction with porous structures using an improved smoothed particle hydrodynamic method[J]. Coastal Engineering, 2014, 88: 88–100. doi: 10.1016/j.coastaleng.2014.02.006
[96] REN B, HE M, DONG P, et al. Nonlinear simulations of wave-induced motions of a freely floating body using WCSPH method[J]. Applied Ocean Research, 2015, 50: 1–12. doi: 10.1016/j.apor.2014.12.003
[97] SHAO S D, JI C M, GRAHAM D I, et al. Simulation of wave overtopping by an incompressible SPH model[J]. Coastal Engineering, 2006, 53(9): 723–735. doi: 10.1016/j.coastaleng.2006.02.005
[98] 段文洋, 王瑞锋, 马山, 等. 规则波中船舶甲板上浪模型试验研究[J]. 哈尔滨工程大学学报, 2013, 34(10): 1209–1213,1260. DUAN W Y, WANG R F, MA S, et al. Model test for green water of ships in regular waves[J]. Journal of Harbin Engineering University, 2013, 34(10): 1209–1213,1260 (in Chinese).
[99] LE TOUZÉ D, MARSH A, OGER G, et al. SPH simulation of green water and ship flooding scenarios[J]. Journal of Hydrodynamics, Ser. B, 2010, 22(5 Supp. 1): 231-236.
[100] AREU-RANGEL O S, HERNÁNDEZ-FONTES J V, SILVA R, et al. Green water loads using the wet dam-break method and SPH[J]. Ocean Engineering, 2021, 219: 108392. doi: 10.1016/j.oceaneng.2020.108392
[101] ZHAO X Z, HU C H. Numerical and experimental study on a 2-D floating body under extreme wave conditions[J]. Applied Ocean Research, 2012, 35: 1–13. doi: 10.1016/j.apor.2012.01.001
[102] ZHAO X Z, YE Z T, FU Y N, et al. A CIP-based numerical simulation of freak wave impact on a floating body[J]. Ocean Engineering, 2014, 87: 50–63. doi: 10.1016/j.oceaneng.2014.05.009
[103] SUI Y T, ZHANG A M, MING F R, et al. Experimental investigation of oblique water entry of high-speed truncated cone projectiles: Cavity dynamics and impact load[J]. Journal of Fluids and Structures, 2021, 104: 103305. doi: 10.1016/j.jfluidstructs.2021.103305
[104] GHAZANFARIAN J, SAGHATCHI R, GORJI-BANDPY M. Turbulent fluid-structure interaction of water-entry/exit of a rotating circular cylinder using SPH method[J]. International Journal of Modern Physics C, 2015, 26(8): 1550088. doi: 10.1142/S0129183115500886
[105] ZHANG H S, ZHANG Z L, HE F, et al. Numerical investigation on the water entry of a 3D circular cylinder based on a GPU-accelerated SPH method[J]. European Journal of Mechanics-B/Fluids, 2022, 94: 1–16. doi: 10.1016/j.euromechflu.2022.01.007
[106] YANG Q Z, XU F, YANG Y, et al. Two-phase SPH model based on an improved Riemann solver for water entry problems[J]. Ocean Engineering, 2020, 199: 107039. doi: 10.1016/j.oceaneng.2020.107039
[107] DI MASCIO A, ANTUONO M, COLAGROSSI A, et al. Smoothed particle hydrodynamics method from a large eddy simulation perspective[J]. Physics of Fluids, 2017, 29(3): 035102. doi: 10.1063/1.4978274
[108] 杨松. 基于SPH方法的回转体结构入水的瞬态流固耦合特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2020. YANG S. Transient fluid-solid interaction characteristics of the water entry of revolved body based on SPH method[D]. Harbin: Harbin Engineering University, 2020 (in Chinese).
[109] WU Q G, NI B Y, BAI X L, et al. Experimental study on large deformation of free surface during water exit of a sphere[J]. Ocean Engineering, 2017, 140: 369–376. doi: 10.1016/j.oceaneng.2017.06.009
[110] CHU X S, YAN K, WANG Z, et al. Numerical simulation of water-exit of a cylinder with cavities[J]. Journal of Hydrodynamics, Ser. B, 2010, 22(Supp.1): 877–881.
[111] SUN P N, LE TOUZÉ D, OGER G, et al. An accurate SPH volume adaptive scheme for modeling strongly-compressible multiphase flows. Part 1: numerical scheme and validations with basic 1D and 2D benchmarks[J]. Journal of Computational Physics, 2021, 426: 109937. doi: 10.1016/j.jcp.2020.109937
[112] 季斌, 程怀玉, 黄彪, 等. 空化水动力学非定常特性研究进展及展望[J]. 力学进展, 2019, 49(1): 428–479. JI B, CHENG H Y, HUANG B, et al. Research progresses and prospects of unsteady hydrodynamics characteristics for cavitation[J]. Advances in Mechanics, 2019, 49(1): 428–479 (in Chinese).
[113] PENG Y X, ZHANG A M, MING F R. Numerical simulation of structural damage subjected to the near-field underwater explosion based on SPH and RKPM[J]. Ocean Engineering, 2021, 222: 108576. doi: 10.1016/j.oceaneng.2021.108576
[114] BENZ W. Smooth particle hydrodynamics: a review[M]//BUCHLER J R. The numerical modelling of nonlinear stellar pulsations. Dordrecht: Springer, 1990: 269-288.
[115] 彭玉祥. 改进的无网格计算方法及其在结构流固耦合冲击毁伤中的应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2019. PENG Y X. Improved mesh free methods and its application in structural damage analysis under fluid-structure impact[D]. Harbin: Harbin Engineering University, 2019 (in Chinese).
[116] XIE W F, LIU T G, KHOO B C. Application of a one-fluid model for large scale homogeneous unsteady cavitation: The modified Schmidt model[J]. Computers & Fluids, 2006, 35(10): 1177–1192.
[117] SUN P N, LE TOUZÉ D, OGER G, et al. An accurate SPH volume adaptive scheme for modeling strongly-compressible multiphase flows. Part 2: extension of the scheme to cylindrical coordinates and simulations of 3D axisymmetric problems with experimental validations[J]. Journal of Computational Physics, 2021, 426: 109936. doi: 10.1016/j.jcp.2020.109936
[118] ZHANG A M, YANG W S, HUANG C, et al. Numerical simulation of column charge underwater explosion based on SPH and BEM combination[J]. Computers & Fluids, 2013, 71: 169–178.
[119] FANG X L, COLAGROSSI A, WANG P P, et al. An accurate and robust axisymmetric SPH method based on Riemann solver with applications in ocean engineering[J]. Ocean Engineering, 2022, 244: 110369. doi: 10.1016/j.oceaneng.2021.110369
[120] MAY D A, MONAGHAN J J. Can a single bubble sink a ship?[J]. American Journal of Physics, 2003, 71(9): 842–849. doi: 10.1119/1.1582187
[121] 王诗平. 水中结构物附近爆炸气泡运动特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2011. WANG S P. Study on dynamics of underwater explosion bubbles near structures[D]. Harbin: Harbin Engineering University, 2011 (in Chinese).
[122] JOSHI S, FRANC J P, GHIGLIOTTI G, et al. SPH modelling of a cavitation bubble collapse near an elasto-visco-plastic material[J]. Journal of the Mechanics and Physics of Solids, 2019, 125: 420–439. doi: 10.1016/j.jmps.2018.12.016
[123] PINEDA S, MARONGIU J C, AUBERT S, et al. Simulation of a gas bubble compression in water near a wall using the SPH-ALE method[J]. Computers & Fluids, 2019, 179: 459–475.
[124] YIN J Y, ZHANG Y X, ZHANG Y N. Numerical study of a laser generated cavitation bubble based on FVM and CLSVOF method[J]. IOP Conference Series:Earth and Environmental Science, 2019, 240(7): 072021.
[125] MÜLLER S, BACHMANN M, KRÖNINGER D, et al. Comparison and validation of compressible flow simulations of laser-induced cavitation bubbles[J]. Computers & Fluids, 2009, 38(9): 1850–1862.
[126] LI T, ZHANG A M, WANG S P, et al. Bubble interactions and bursting behaviors near a free surface[J]. Physics of Fluids, 2019, 31(4): 042104. doi: 10.1063/1.5088528
[127] TIAN Z L, LIU Y L, ZHANG A M, et al. Analysis of breaking and re-closure of a bubble near a free surface based on the Eulerian finite element method[J]. Computers & Fluids, 2018, 170: 41–52.
[128] LIBERSKY L D, PETSCHEK A G. Smooth particle hydrodynamics with strength of materials[M]. Advances in the free-Lagrange method including contributions on adaptive gridding and the smooth particle hydrodynamics method. Springer, Berlin, Heidelberg, 1991: 248-257.
[129] MAUREL B, COMBESCURE A. A SPH shell formulation for plasticity and fracture analysis in explicit dynamics[J]. International Journal for Numerical Methods in Engineering, 2008, 76(7): 949–971. doi: 10.1002/nme.2316
[130] CALEYRON F, COMBESCURE A, FAUCHER V, et al. Dynamic simulation of damage-fracture transition in smoothed particles hydrodynamics shells[J]. International Journal for Numerical Methods in Engineering, 2012, 90(6): 707–738. doi: 10.1002/nme.3337
[131] MING F R, ZHANG A M, WANG S P. Smoothed particle hydrodynamics for the linear and nonlinear analyses of elastoplastic damage and fracture of shell[J]. International Journal of Applied Mechanics, 2015, 7(2): 1550032. doi: 10.1142/S1758825115500325
[132] MING F R, ZHANG A M, XUE Y Z, et al. Damage characteristics of ship structures subjected to shockwaves of underwater contact explosions[J]. Ocean Engineering, 2016, 117: 359–382. doi: 10.1016/j.oceaneng.2016.03.040
[133] CALEYRON F. Simulation numérique par la méthode SPH de fuites de fluide consécutives à la déchirure d'un réservoir sous impact[D]. Villeurbanne, France: INSA de Lyon, 2011.
[134] HUANG Y H, ZHANG Z G, PENG Y X, et al. A three-dimensional beam formulation for large deformation and an accurate implementation of the free boundary[J]. International Journal of Non-Linear Mechanics, 2021, 134: 103736. doi: 10.1016/j.ijnonlinmec.2021.103736
[135] PENG Y X, ZHANG A M, MING F R. A thick shell model based on reproducing kernel particle method and its application in geometrically nonlinear analysis[J]. Computational Mechanics, 2018, 62(3): 309–321. doi: 10.1007/s00466-017-1498-9
[136] PENG Y X, ZHANG A M, LI S F, et al. A beam formulation based on RKPM for the dynamic analysis of stiffened shell structures[J]. Computational Mechanics, 2019, 63(1): 35–48. doi: 10.1007/s00466-018-1583-8
[137] GUO K, SUN P N, CAO X Y, et al. A 3-D SPH model for simulating water flooding of a damaged floating structure[J]. Journal of Hydrodynamics, Ser. B, 2017, 29(5): 831–844. doi: 10.1016/S1001-6058(16)60795-3
[138] CHENG H, ZHANG A M, MING F R. Study on coupled dynamics of ship and flooding water based on experimental and SPH methods[J]. Physics of Fluids, 2017, 29(10): 107101. doi: 10.1063/1.4986004
[139] MING F R, ZHANG A M, CHENG H, et al. Numerical simulation of a damaged ship cabin flooding in transversal waves with smoothed particle hydrodynamics method[J]. Ocean Engineering, 2018, 165: 336–352. doi: 10.1016/j.oceaneng.2018.07.048
[140] CAO X Y, TAO L B, ZHANG A M, et al. Smoothed particle hydrodynamics (SPH) model for coupled analysis of a damaged ship with internal sloshing in beam seas[J]. Physics of Fluids, 2019, 31(3): 032103. doi: 10.1063/1.5079315
[141] CAO X Y, MING F R, ZHANG A M, et al. Multi-phase SPH modelling of air effect on the dynamic flooding of a damaged cabin[J]. Computers & Fluids, 2018, 163: 7–19.
[142] HUANG C, ZHAO L, NIU J P, et al. Coupled particle and mesh method in an Euler frame for unsteady flows around the pitching airfoil[J]. Engineering Analysis with Boundary Elements, 2022, 138: 159–176. doi: 10.1016/j.enganabound.2022.02.011
[143] MARRONE S, DI MASCIO A, LE TOUZÉ D. Coupling of smoothed particle hydrodynamics with finite volume method for free-surface flows[J]. Journal of Computational Physics, 2016, 310: 161–180. doi: 10.1016/j.jcp.2015.11.059
[144] ZHUANG Y, WAN D C. Parametric study of a new HOS-CFD coupling method[J]. Journal of Hydrodynamics, 2021, 33(1): 43–54. doi: 10.1007/s42241-021-0012-1
-
期刊类型引用(7)
1. 黄晓婷，孙鹏楠，邱艳宇，熊自明. 柱形装药水下爆炸近场荷载SPH数值模拟研究. 华中科技大学学报(自然科学版). 2025(04): 8-14 . 
百度学术
2. 吴诗贤，黄敏沾，尹家栋，梅璇，周珉立，孙鹏楠. 科考船极端海况下砰击载荷与液体飞溅特性数值模拟. 中国舰船研究. 2025(02): 175-186 . 本站查看
3. 管祥善，孙鹏楠，李江昊，孙龙泉. 基于光滑粒子流体动力学的波浪中航行体入水数值模拟. 空气动力学学报. 2024(02): 85-95 . 百度学术
4. 王琰，蒋海燕，韩璐，苏健军，杨峰. 爆炸冲击波作用下板架结构响应研究综述. 兵器装备工程学报. 2024(03): 151-160 . 百度学术
5. 李营，杜志鹏，陈赶超，王诗平，侯海量，李晓彬，张攀，张伦平，孔祥韶，李海涛，郭君，姚术健，王志凯，殷彩玉. 舰艇爆炸毁伤与防护若干关键问题研究进展. 中国舰船研究. 2024(03): 3-60 . 本站查看
6. 黄晓婷，孙鹏楠，吕鸿冠. 考虑气体压缩性的多相δ~+-SPH模型及应用. 中国造船. 2024(06): 235-243 . 百度学术
7. 黄杰，李明鸿，吴拓展，宗周红. 钙质砂场地爆炸成坑实验与数值模拟研究. 爆炸与冲击. 2023(10): 30-45 . 百度学术
其他类型引用(9)
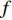
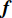
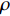
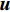
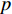
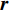
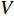
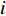
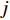
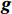
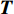
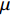
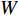
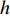
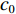
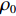
下载:
计量
- 文章访问数: 1980
- HTML全文浏览量: 839
- PDF下载量: 412
- 被引次数: 16
