0.   引　言

无人船（unmanned surface vehicles，USVs）作为一种探索海洋、开发海洋的工具，具有低成本、智能化和灵活性强等优点，在代替人类执行危险、耗时和繁重的作业任务时具有显著优势^[1]。多艘无人船通过协同控制以编队的形式进行作业更具有优势，成为未来发展的必然趋势^[2-4]。根据多无人船运动场景的不同，可以将多无人船的运动控制分为协同轨迹跟踪^[5-8]、协同目标跟踪^[9-10]和协同路径跟踪^[11-16]。其中，协同路径跟踪控制是指驱动多艘无人船跟踪一条或多条参数化的预设路径，并保持期望队形，近年引起研究人员的广泛关注。

针对多无人船的协同路径跟踪控制问题，国内外学者已经取得了一些研究成果。Gu等^[12]针对欠驱动无人船的协同路径跟踪问题，提出了一种具有内外环结构的抗干扰协同路径跟踪控制器，在外环设计了视距制导律，在内环设计了基于扩张状态观测器的抗扰控制律，通过有向通信拓扑传输路径参数来实现协同控制。Liu等^[14]提出一种模块化自适应控制方法，通过自适应项和回声状态网络分别估计不确定的运动学和未知的动力学项，并设计协同路径操纵控制器，实现沿参数化路径的队列编队模式。Chen等^[16]研究了全驱动无人船沿闭合路径恒速协同运动并保持航向同步的问题，在双向通信拓扑结构下，提出一种基于共识的自适应控制方法，用于估计参考速度，使得参考速度无需全局已知。值得注意的是，上述协同路径跟踪控制方法在协同层采用连续或者周期性的通信方式，会持续占用网络通信带宽资源。然而对于海洋环境中航行的多无人船，通常采用海上自组网的无线通信方式。无人船之间，无人船和远程控制中心之间的信息传输不可避免地会占用通信网络带宽。随着编队中无人船数量的增加，网络带宽受限问题将会越发明显。此外，无线通信的性能会随着通信距离的增加及受复杂海洋环境和气象条件的影响而下降^[17]。工作在海洋环境中的无人船编队面临着海上通信带宽受限的挑战。

事件触发控制为解决通信网络占用问题提供了可行的解决方法，引起了学者的关注。Praveen等^[18]提出一种分散式事件触发的协同路径跟踪控制器，可减少无人船之间的信息交换次数。Ma等^[19]针对网络化控制的无人船提出基于事件触发的模糊控制方法，可减少通过网络的采样次数和控制次数。Liu等^[20]针对无人船的状态和扰动估计问题提出基于事件触发的扩张状态观测器，可减少采样次数和计算次数。值得一提的是，上述事件触发机制所设计的触发条件都是静态的。虽然静态事件触发机制能够减轻通信负担，但当无人船协同趋于一致时，会使触发阈值变小从而触发大量不必要的事件。因此，需要探索设计更灵活的事件触发机制，以进一步减少触发次数。

另外，在无人船跟踪给定路径的过程中，会受到风、浪、海流等外部环境扰动的影响；此外，由于无人船的数学模型无法精确获得，模型内部存在水动力系数变化和未建模动态引起的不确定性，给无人船的运动控制带来了严峻挑战^[21]。协同路径跟踪控制的性能很大程度上受无人船动力学不确定性和外部扰动的影响，甚至会导致控制的不稳定。为了提高无人船控制层的控制精度, 保证控制的稳定性，研究人员提出了各种解决不确定性和扰动的方法，主要有神经网络控制^[5-6]、模糊控制^[10-19]、自抗扰控制^[12-13]、自适应控制^[14-15]、滑模控制^[22-23]等。

本文将针对网络带宽资源受限、模型参数不确定和环境扰动情况下的多无人船协同路径跟踪控制问题，提出一种基于动态事件触发的协同路径跟踪控制方法。本文的主要贡献为：1）针对网络带宽资源受限的问题，提出一种基于动态事件触发的协同路径更新律，以非周期方式通信，只在预定义事件满足的情况下才会进行通信，因此能够有效降低网络通信量。所提的动态事件触发机制通信通过引入动态变量，在兼顾系统性能的同时，增大系统稳态时的通信间隔，进一步降低网络通信量。2）针对无人船模型参数不确定和受环境扰动的问题，提出基于超螺旋观测器的动力学抗扰控制方法，能够在有限时间内实现无人船的动力学跟踪控制，改善控制子系统的性能。

1.   问题描述

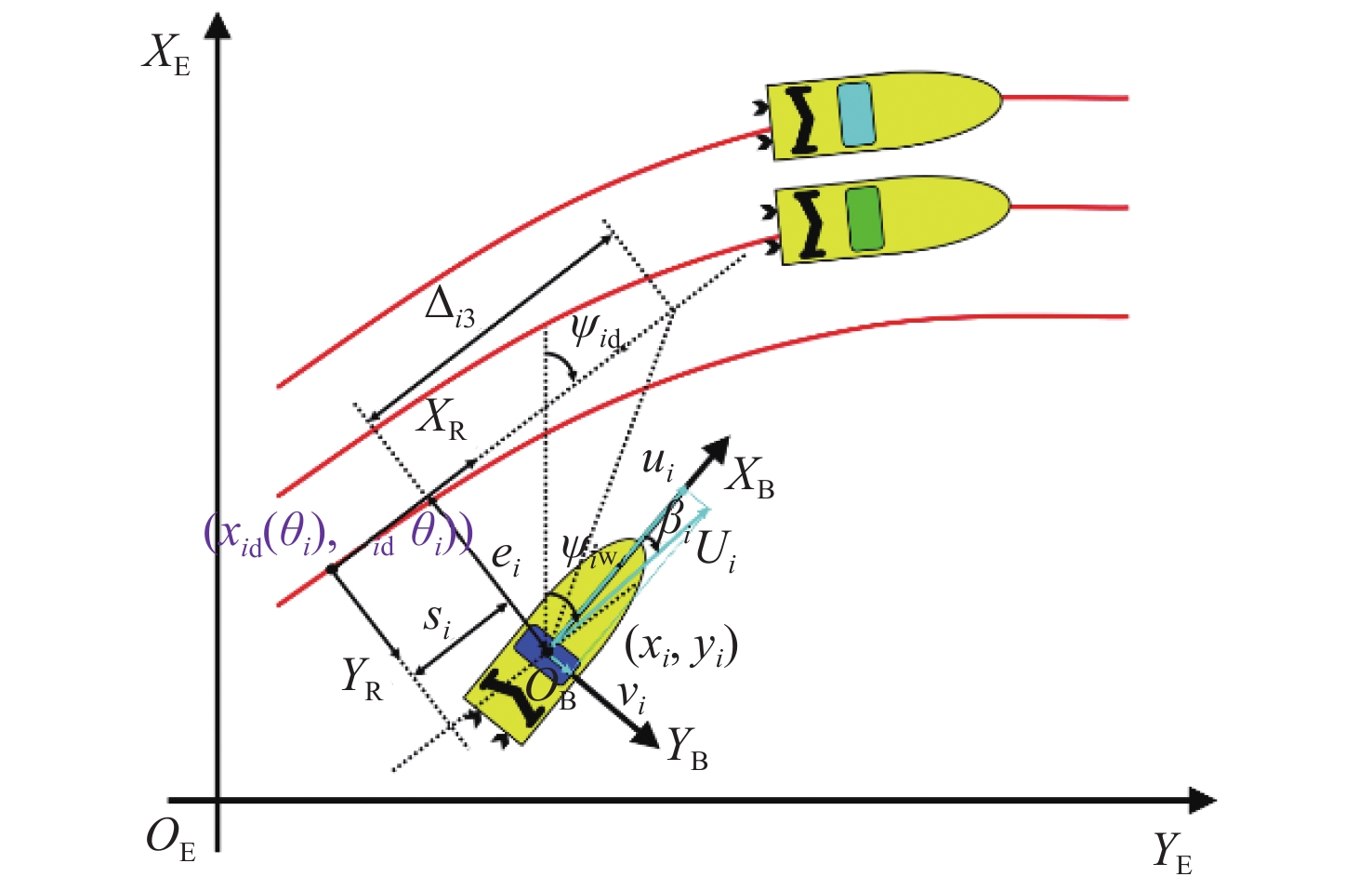
考虑一个由N艘欠驱动无人船组成的系统，如图1所示，无人船编号为1，…，N。其中，无人船在水平面进行三自由度运动。图中，第i艘无人船的运动学和动力学模型可以表示为：

图  1  无人船协同路径跟踪

Figure  1.  The cooperative path following of the USVs

下载: 全尺寸图片 幻灯片

和

式中：${x_i}$，${y_i}$为无人船在北东地（NED）坐标系${\text{(}}{O_{\text{E}}} - {X_{\text{E}}}{Y_{\text{E}}})$下的位置坐标；${\psi _{i{\text{w}}}} \in ( - {\text{π}} ,{\text{π}} ]$为无人船的航迹角；${U_i} = \sqrt {u_i^2 + v_i^2}$为无人船的合速度；${\beta _i} =$ ${\text{atan2}}({v_i},{u_i})$为侧滑角；${u_i},{v_i},{r_i}$分别为无人船在船体坐标系$({O_{\text{B}}} - {X_{\text{B}}}{Y_{\text{B}}})$下的纵荡速度、横荡速度和艏摇角速度；${m_{iu}},{m_{iv}},{m_{ir}}$分别为无人船在纵荡方向的质量、横荡方向的质量和转动惯量；${f_{iu}}( \cdot ),{f_{iv}}( \cdot ),{f_{ir}}( \cdot )$为无人船模型中的未知非线性函数，与无人船水动力阻尼力、科里奥利力以及未建模流体动力学相关；${d_{iu}},{d_{iv}},{d_{ir}}$为由风、浪和海流引起的时变环境扰动；${\tau _{iu}}$和${\tau _{ir}}$分别表示无人船的纵荡推力和艏摇力矩。

如图1所示，多艘无人船沿着多条参数化路径$(x_{i\mathrm{d}}(\theta_i),y_{i\mathrm{d}}(\theta_i))$运动，并保持并排队形以完成协同路径跟踪任务，其中${\theta _i} \in {\bf{R}}$表示路径参数。考虑一个虚拟领导船，虚拟领导船的路径参数${\theta _0}$的更新动态定义为${\dot {\boldsymbol{\theta}} _0} = {v_0}$，其中${v_0} \in {{\bf{R}}^ + }$为路径参数的更新速度。

定义路径切向坐标系${\text{(}}{X_{\text{R}}}{Y_{\text{R}}})$下的路径跟踪误差为

式中：${s_i}$和${e_i}$分别为横向和纵向路径跟踪误差；$\psi_{i\mathrm{d}}=\text{atan2}\left(y'_{i\mathrm{d}}(\theta_i),x'_{i\mathrm{d}}(\theta_i)\right)$为路径的切向角，其中，$y'_{i\mathrm{d}}(\theta_i)$和$x'_{i\mathrm{d}}(\theta_i)$为路径的偏导数，$y'_{i\mathrm{d}}(\theta_i)={\partial}y_{i\mathrm{d}}(\theta_i)/{\partial}\theta_i$，$x'_{i\mathrm{d}}(\theta_i)=\partial x_{i\mathrm{d}}(\theta_i)/\partial\theta_i$。

本文的目的是设计动态事件触发的协同路径跟踪控制器，实现如下控制目标。

1） 路径跟踪目标：驱动第i艘无人船跟踪第i个参考路径，使得

式中，${\delta _1},{\delta _2} \in {{\bf{R}}^ + }$为小常数。

2） 速度目标：使得第i艘无人船的路径参数更新速度趋于虚拟领导船的速度${v_0}$，满足

式中，${\delta _3} \in {{\bf{R}}^ + }$为一个小常数。

3） 协同目标：驱动第i艘无人船通过有向通信拓扑实现期望的队形，使得

式中，${\delta _4} \in {{\bf{R}}^ + }$为一个小常数。

2.   控制器设计

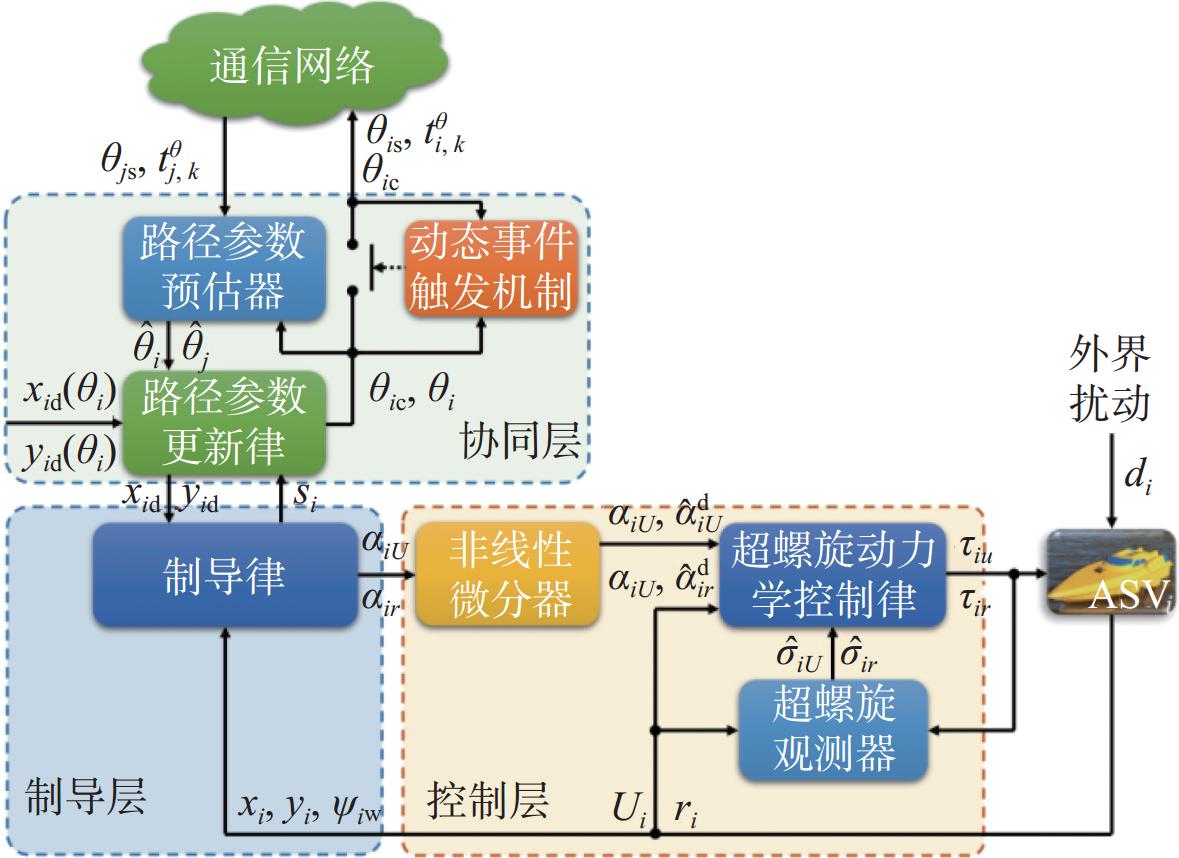
本节将设计基于动态事件触发的多无人船协同路径跟踪控制器，实现上文的控制目标。本节控制器设计分为协同层、制导层和控制层，所设计的基于动态事件触发的多无人船协同路径跟踪控制器结构框架如图2所示，图中部分变量解释见本章公式。

图  2  动态事件触发多无人船协同路径跟踪控制器结构框架

Figure  2.  Structure of the dynamic event-triggered cooperative path following controller for multiple USVs

下载: 全尺寸图片 幻灯片

2.1   协同层设计

定义分布式路径参数协同误差$\theta_{i\mathrm{e}}(t)= \Sigma_{j\in\mathcal{N}_i}a_{ij}\left(\theta_i(t)-\theta_j(t)\right)+b_i\left(\theta_i(t)-\theta_0(t)\right)$，其中${a_{ij}}$为无人船之间的通信关系，如果无人船i能收到无人船j的信息，则${a_{ij}} = 1$，否则${a_{ij}} = 0$；${b_i}$为无人船和虚拟领导船之间的通信关系，如果无人船i能收到虚拟领导船的信息，则${b_i} = 1$，否则，${b_i} = 0$。从定义的协同误差可以看出，需要连续地获取$j \in {\mathcal{N}_i}$艘邻居无人船的路径参数，其中，${\mathcal{N}_i}$为第i艘无人船的邻居船集合。为了降低网络通信量，设计一个路径参数预估器：

式中，$\theta_{j\mathrm{s}}(t_k^j)$为第j艘无人船在$t_k^j$时刻通信的路径信息。

定义一个基于预估器的协同误差为${\theta _{i{\mathrm{c}}}}(t) = \sum\limits_{j \in {N_i}} {} {a_{ij}}( {\hat \theta _i^i(t) - \hat \theta _j^i(t)} ) + {b_i}( {\hat \theta _i^i(t) - {\theta _0}(t)} )$。设计第i艘无人船的动态事件触发路径参数更新律：

式中：$k_{i1}^\theta ,k_{i2}^\theta \in {{\bf{R}}^ + }$为控制参数；${\omega _i}$为协同项；$\theta_{i\mathrm{c}}^s$为触发的协同误差。

为了减少通信次数，实现非周期协同控制，在静态事件触发机制的基础上，引入一个动态变量${\eta _{i\theta }}$，设计如下的动态事件触发机制：

式中：${\rho _{i\eta }} \in {{\bf{R}}^ + }$为参数；$0 < {\xi _{i\theta }} < 1$为动态事件触发阈值；${\varsigma _{i\theta }}(t) = \theta _{i{\mathrm{c}}}^{\mathrm{s}}(t) - {\theta _{i{\mathrm{c}}}}(t)$为测量误差；${\varepsilon _{i\theta }} \in {{\bf{R}}^ + }$为小参数；$t_{k + 1}^i$为下一次的通信时刻，$t_k^i$为最近一次的通信时刻，并且有$t_1^i = 0$。

2.2   制导层设计

利用式（1）和式（3），可得${s_i}$和${e_i}$对时间的导数

式中，${U_{i{\mathrm{d}}}} = \sqrt {x_{i{\mathrm{d}}}^{\prime 2}({\theta _i}) + y_{i{\mathrm{d}}}^{\prime 2}({\theta _i})}$为路径的速度。

定义动力学跟踪误差${z_{iU}} = {U_i} - {\alpha _{iU}}$，${z_{ir}} = {r_i} - {\alpha _{ir}}$和航迹角跟踪误差$\psi_{i\mathrm{e}}=\psi_{i\text{w}}-\alpha_{i\psi}$，其中${\alpha _{iU}}$，${\alpha _{ir}}$和${\alpha _{i\psi }}$是制导信号，则式（10）可以整理为

式中：${\varrho _{i2}} = \sin ({\psi _{i{\text{w}}}} - {\psi _{i{\mathrm{d}}}}) - \sin ({\alpha _{i\psi }} - {\psi _{i{\mathrm{d}}}})$；${\varrho _{i1}} =$ ${\sin ^2}(\psi _{i{\text{w}}} / 2 - {{\psi _{i{\mathrm{d}}}}} / 2)$。

为了稳定式（11），设计基于视距制导方法^[24]（line of sight，LOS）的制导律：

式中：${k_{i1}},{k_{i2}} \in {{\bf{R}}^ + }$为控制增益；${\varDelta _{i1}},{\varDelta _{i2}} \in {{\bf{R}}^ + }$为常数；${\varDelta _{i3}} \in {{\bf{R}}^ + }$为前视距离。

2.3   控制层设计

通过前一节的设计，获得了无人船的制导信号。为了获取制导信号的导数信息，将制导信号通过以下非线性微分器进行计算：

式中：$\hat{\alpha}_{iU},\hat{\alpha}_{iU}^{\mathrm{d}}$和$\hat{\alpha}_{ir},\hat{\alpha}_{ir}^{\mathrm{d}}$分别为${\alpha _{iU}},{\dot \alpha _{iU}}$和${\alpha _{ir}},{\dot \alpha _{ir}}$的估计值；$\rho _{i1}^U,\;\rho _{i2}^U,\;\rho _{i1}^r,\;\rho _{i2}^r \in {{\bf{R}}^ + }$为微分器参数；${\tilde \alpha _{iU}} = {\hat \alpha _{iU}} - {\alpha _{iU}}$和${\tilde \alpha _{ir}} = {\hat \alpha _{ir}} - {\alpha _{ir}}$为微分器的估计误差；$\left\lceil {\cdot} \right\rfloor^{\chi }= \text{sign}(\cdot){|\cdot|}^{\chi },\chi > 0$，其中$\text{sign}(\cdot)$表示符号函数。

将无人船的动力学模型式（2）改写为

式中：${\sigma _{iU}} = m_{iu}^{ - 1}\left[ {{f_{iu}}({u_i},{v_i},{r_i}) + {d_{iu}}} \right]\cos {\beta _i} - 2m_{iu}^{ - 1}{\tau _{iu}}\cdot$ ${\sin ^2}{{({\beta _i}} /{2)}} + m_{iv}^{ - 1}\left[ {{f_{iv}}({u_i},{v_i},{r_i}) + {d_{iv}}} \right]\sin {\beta _i}$和${\sigma _{ir}} = m_{ir}^{ - 1}{f_{ir}}({u_i}, {v_i},{r_i}) + m_{ir}^{ - 1}{d_{ir}}$为无人船受到的总扰动，包括内部模型不确定性和外部环境扰动。

为了在有限时间内估计模型式（14）中的总扰动，设计如下超螺旋观测器：

式中：${\hat U_i}$, ${\hat r_i}$和${\hat \sigma _{iU}}$, ${\hat \sigma _{ir}}$分别为${U_i}$, ${r_i}$和${\sigma _{iU}}$, ${\sigma _{ir}}$的估计值；$k_{i1}^U$, $k_{i2}^U$, $k_{i1}^r$, $k_{i2}^r \in {{\bf{R}}^ + }$为观测器增益；${\tilde U_i} = {\hat U_i} - {U_i}$和${\tilde r_i} = {\hat r_i} - {r_i}$为观测器的估计误差。

定义滑模面${z_{iU}} = {U_i} - {\alpha _{iU}}$和${z_{ir}} = {r_i} - {\alpha _{ir}}$，利用式（14），可得${z_{iU}}$和${z_{ir}}$对时间的导数为

为了稳定${z_{iU}}$和${z_{ir}}$，设计基于超螺旋的动力学控制律：

式中：${\eta _{iu}},\;{\eta _{ir}}$为控制器的辅助状态变量；$k_{i1}^{{\mathrm{c}}u},\;k_{i2}^{{\mathrm{c}}u}, k_{i1}^{{\mathrm{c}}r},\;k_{i2}^{{\mathrm{c}}r} \in {{\bf{R}}^ + }$为控制器增益。

3.   稳定性分析

本节将分析整个闭环系统的稳定性。为了进行稳定性分析，作如下假设。

假设1：${\sigma _{iU}},\;{\sigma _{ir}},\;{\dot \alpha _{iU}},\;{\dot \alpha _{ir}}$的导数是有界的，满足$\left| {{{\dot \sigma }_{iU}}} \right| \leqslant \sigma _{iU}^*$, $\left| {{{\dot \sigma }_{ir}}} \right| \leqslant \sigma _{ir}^*,$ $\left| {{{\ddot \alpha }_{iU}}} \right| \leqslant \alpha _{iU}^*,\;\left| {{{\ddot \alpha }_{ir}}} \right| \leqslant \alpha _{ir}^*$，其中$\sigma _{iU}^*$, $\sigma _{ir}^*,\;\alpha _{iU}^*,\;\alpha _{ir}^* \in {{\bf{R}}^ + }$。

3.1   协同子系统稳定性分析

定义$\boldsymbol{\theta}=\left[\theta_1,\ldots,\theta_N\right]^{\mathrm{T}}$, $\boldsymbol{\theta}_{\mathrm{e}}=\left[\theta_{1\mathrm{ }\mathrm{e}},\ldots,\theta_{N\mathrm{e}}\right]^{\mathrm{T}}$，则协同误差可以写成向量形式：

式中：$\mathcal{L}$为通信图的拉普拉斯矩阵；$\mathcal{B} = {\text{diag}}\{ {b_1}, \ldots , {b_N} \}$；${{\mathbf{1}}_N}$为元素为1的n维列向量；$\otimes$为克罗内克积。

定义$\boldsymbol{\omega}=\left[\omega_1,\ldots,\omega_N\right]\mathrm{^T}$，$\mathcal{H} = \mathcal{L} + \mathcal{B}$，对$\boldsymbol{\theta}_{\mathrm{e}}$求时间的导数，可得

将式（8）代入，可得协同子系统误差动态为

式中：${{\boldsymbol{A}}_\theta }{\text{ = }} - \mathcal{H}{\boldsymbol{k}}_2^\theta$；${{\boldsymbol{B}}_\theta }{\text{ = }}\mathcal{H}k_1^\theta$；$\boldsymbol{\varsigma}_{\theta}=[\varsigma_{1\theta},\ldots,\varsigma_{N\theta}]^{\mathrm{T}}$；$\tilde{\boldsymbol{\theta}}=[\tilde{\theta}_1,\ldots,\tilde{\theta}_N]\mathrm{^T}$；$\boldsymbol{s}=[s_1,\ldots,s_N]^{\mathrm{T}}$，其中${\boldsymbol{k}}_1^\theta = {\text{diag}}\{ k_{11}^\theta , \ldots , k_{N1}^\theta \}$，${\boldsymbol{k}}_2^\theta = {\text{diag}}\{ {k_{12}^\theta , \ldots ,k_{N2}^\theta } \}$，${\tilde \theta _i} = \sum\limits_{j \in {N_i}} {} {a_{ij}}\tilde \theta _j^i(t)$，$\tilde \theta _j^i(t) = {\theta _j}(t) - \hat \theta _j^i(t)$。由于矩阵${{\boldsymbol{A}}_\theta }$是赫尔维兹矩阵，则存在正定对称矩阵${{\boldsymbol{P}}_\theta } \in {{\bf{R}}^{N \times N}}$，满足${\boldsymbol{A}}_\theta ^{\mathrm{T}}{{\boldsymbol{P}}_\theta } + {{\boldsymbol{P}}_\theta }{{\boldsymbol{A}}_\theta } \leqslant - {\varepsilon _1}{{\boldsymbol{I}}_N}$，其中${\varepsilon _1} \in {{\bf{R}}^ + }$。

协同子系统式（20）的稳定性由以下引理给出。

引理1：协同子系统式（20），以${{\boldsymbol{\varsigma}}_\theta },\tilde {\boldsymbol{\theta}} ,{\boldsymbol{s}}$为输入，$\boldsymbol{\theta}_{\mathrm{e}}$为状态，是输入–状态稳定的。

证明：构建李雅普诺夫函数：

利用式（20），对${V_\theta }$求时间的导数：

当满足以下条件时，

将式（23）代入式（22），可得

式中，$0 < {\ell _1} < 1$。

对$\tilde \theta _j^i$求时间的导数，可得$\dot \tilde \theta _j^i(t) = k_{j1}^\theta ( {{s_j}(t) - {s_j}(t_{j,k}^\theta )} )$，由引理2可知，s是有界的。可得$\dot \tilde \theta _j^i(t) \leqslant 2k_{j1}^\theta | {{s_j}} |$，$| {\tilde \theta _j^i} | \leqslant 2k_{j1}^\theta (t - t_{j,k}^\theta )| {{s_j}} |$，即$\tilde \theta$有界。根据事件触发机制式（9），可知输入${{\boldsymbol{\varsigma}}_\theta }$有界。因此，可以得出协同子系统式（20）输入–状态稳定，且系统状态满足

式中：${\gamma _1}$是$\mathcal{K}\mathcal{L}$类函数；${\kappa ^s},{\kappa ^{\tilde \theta }}$是$\mathcal{K}$类函数，定义为

3.2   制导子系统稳定性分析

将式（12）代入式（11），可以得到制导子系统的误差动态：

式中：$k_{i1}^{\mathrm{L}}=k_{i1}/\sqrt{s_{i\mathrm{s}}^2+\mathit{\Delta}_{i1}^2}$, $k_{i2}^{\mathrm{L}}=k_{i2}/\sqrt{\psi_{i\mathrm{e}}^2+\mathit{\Delta}_{i2}^2}$, $k_{i3}^{\mathrm{L}}= U_i/\sqrt{e_{i\mathrm{s}}^2+\mathit{\Delta}_{i3}^2}$。

定义$\boldsymbol{h}_i=\left[U_{i\mathrm{d}}w_i,U_i\varrho_{i2},\; \dot{\beta}_i\right]\mathit{^{\mathrm{T}}\mathrm{ }}$，$\boldsymbol{E}_{i1}=\left[s_i,e_i,\psi_{i\mathrm{e}}\right]\mathrm{^T}$, $\boldsymbol{z}_i=\left[{z}_{iU},\; {z}_{ir}\right]^{\mathrm{T}}$，则式（27）可写成向量形式：

其中：

运动学制导子系统式（28）的稳定性由以下引理给出。

引理2：运动学制导子系统式（28），以${{\boldsymbol{z}}_i}$和${{\boldsymbol{h}}_i}$为输入，以${{\boldsymbol{E}}_{i1}}$为状态，是输入−状态稳定的。

证明：构建李雅普诺夫函数：

利用式（28），对${V_{i1}}$求时间的导数，可得

当满足以下条件时，

将式（31）代入式（30），可得

式中，$0 < {\ell _{i2}} < 1$。根据假设1和引理1可知，输入${{\boldsymbol{h}}_i}$是有界的。${{\boldsymbol{z}}_i}$的有界性由引理5保证。因此，可以得出运动学制导子系统式（28）输入−状态稳定，且系统状态满足

式中：${\gamma _2}$是$\mathcal{K}\mathcal{L}$类函数；${\kappa ^z},{\kappa ^h}$是$\mathcal{K}$类函数，定义为

3.3   非线性微分器子系统稳定性分析

定义微分器的估计误差为$\tilde{\alpha}_{iU}^{\mathrm{d}}=\hat{\alpha}_{iU}^{\mathrm{d}}-\dot{\alpha}_{iU}$和$\tilde{\alpha}_{ir}^{\mathrm{d}}=\hat{\alpha}_{ir}^{\mathrm{d}}-\dot{\alpha}_{ir}$，根据式（13），可以得到非线性微分器子系统的误差动态为

式（35）与式（36）有相同的形式，稳定性证明过程相似，在此直接给出结论。

引理3：在满足假设1的前提下，非线性微分器子系统式（35），以${\ddot \alpha _{iU}},\;{\ddot \alpha _{ir}}$为输入，以$\tilde{\alpha}_{iU},\; \tilde{\alpha}_{iU}^{\mathrm{d}},\; \tilde{\alpha}_{ir}, \tilde{\alpha}_{ir}^{\mathrm{d}}$为状态，是有限时间收敛的。估计误差$\tilde{\alpha}_{iU}, \tilde{\alpha}_{iU}^{\mathrm{d}}$和$\tilde{\alpha}_{ir},\; \tilde{\alpha}_{ir}^{\mathrm{d}}$分别在有限时间$T_{i1}^U$和$T_{i1}^r$内收敛到0。

3.4   估计子系统稳定性分析

定义观测器估计误差为${\tilde \sigma _{iU}} = {\hat \sigma _{iU}} - {\sigma _{iU}}$和${\tilde \sigma _{ir}} = {\hat \sigma _{ir}} - {\sigma _{ir}}$，根据式（14）和式（15），可以得到超螺旋观测器估计子系统的误差动态为

定义$\boldsymbol{E}_{i 2}^U=\left[{\left\lceil{\tilde{U}_i}\right\rfloor} ^{\tfrac{1}{2}}, \tilde{\sigma}_{i U}\right]^{\mathrm{T}},\; \boldsymbol{E}_{i 2}^r=\left[{\left\lceil{\tilde{r}_i}\right\rfloor} ^{\tfrac{1}{2}},\; \tilde{\sigma}_{i r}\right]^{\mathrm{T}}$, ${\varsigma _{iU}}{\text{ = }} {\left| {{{\tilde U}_i}} \right|^{ - \tfrac{1}{2}}},\;{\varsigma _{ir}}{\text{ = }}{\left| {{{\tilde r}_i}} \right|^{ - \tfrac{1}{2}}}$，${\mu _{iU}} = {\dot \sigma _{iU}}{\left| {{{\tilde U}_i}} \right|^{\tfrac{1}{2}}},\;{\mu _{ir}} = {\dot \sigma _{ir}}{\left| {{{\tilde r}_i}} \right|^{\tfrac{1}{2}}}$，则式（36）可写成向量形式：

其中：

由假设1可得，${\mu _{iU}},\;{\mu _{ir}}$满足$| {{\mu _{iU}}} | < | {{{\bar \mu }_{iU}}} | <\sigma _{iU}^*\| {{\boldsymbol{E}}_{i2}^U} \|$, $| {{\mu _{ir}}} | < | {{{\bar \mu }_{ir}}} | < \sigma _{ir}^*\| {{\boldsymbol{E}}_{i2}^r} \|$，其中，$| {{{\bar \mu }_{iU}}} |{\text{ = }}\sigma _{iU}^*{| {{{\tilde U}_i}} |^{\tfrac{1}{2}}}$, $| {{{\bar \mu }_{ir}}} | = \sigma _{ir}^*{| {{{\tilde r}_i}} |^{\tfrac{1}{2}}}$，故有$\sigma _{iU}^{*2}{\| {{\boldsymbol{E}}_{i2}^U} \|^2} - {| {{\mu _{iU}}} |^2} > 0, \sigma _{ir}^{*2}{\| {{\boldsymbol{E}}_{i2}^r} \|^2} - {| {{\mu _{ir}}} |^2} > 0$成立。注意到子系统${\boldsymbol{E}}_{i2}^U$和${\boldsymbol{E}}_{i2}^r$有相同的形式，在此以子系统${\boldsymbol{E}}_{i2}^U$为例给出详细分析过程。

引理4：在满足假设1的前提下，若存在正定对称矩阵${\boldsymbol{P}}_{i2}^U,{\boldsymbol{Q}}_{i2}^U \in {{\bf{R}}^{2 \times 2}}$使等式$\boldsymbol{A}_{i2}^{U\mathrm{T}}\boldsymbol{P}_{i2}^U+\boldsymbol{P}_{i2}^U\boldsymbol{A}_{i2}^U+\boldsymbol{P}_{i2}^U\boldsymbol{B}_{iU} \boldsymbol{B}_{iU}^{\mathrm{T}}\boldsymbol{P}_{i2}^U+\overline{\mu}_{iU}^2\boldsymbol{C}_{iU}^{\mathrm{T}}\boldsymbol{C}_{iU}=-\boldsymbol{Q}_{i2}^U$成立，其中${{\boldsymbol{C}}_{iU}} = \left[ {{\text{0,1}}} \right]$。则超螺旋观测器估计子系统${\boldsymbol{E}}_{i2}^U$，以${\mu _{iU}}$为输入，以${\boldsymbol{E}}_{i2}^U$为状态，是有限时间收敛的。

证明：构建李雅普诺夫函数：

利用式（37），对$V_{i2}^U$求时间的导数，可得

将不等式${\varsigma _{iU}}\left\| {{\boldsymbol{E}}_{i2}^U} \right\| > 1$代入式（39），可得

因为式(38)为二次正定函数，故有${\lambda _{\min }}\left( {{\boldsymbol{P}}_{i2}^U} \right){\left\| {{\boldsymbol{E}}_{i2}^U} \right\|^2} \leqslant V_{i2}^U \leqslant {\lambda _{\max }}\left( {{\boldsymbol{P}}_{i2}^U} \right){\left\| {{\boldsymbol{E}}_{i2}^U} \right\|^2}$，由此可得$\left\| {{\boldsymbol{E}}_{i2}^U} \right\| \geqslant \sqrt {{{V_{i2}^U} \mathord{\left/ {\vphantom {{V_{i2}^U} {{\lambda _{\max }}}}} \right. } {{\lambda _{\max }}}}\left( {{\boldsymbol{P}}_{i2}^U} \right)}$。将所得不等式继续代入式（40），可得

因此，状态${\boldsymbol{E}}_{i2}^U$在有限时间$T_{i2}^U \leqslant 2{\sqrt {{\lambda _{\max }}\left( {{\boldsymbol{P}}_{i2}^U} \right)} } / {{\lambda _{\min }}}\left( {{\boldsymbol{Q}}_{i2}^U} \right)V_{i2}^{U\tfrac{1}{2}}(0)$内收敛到零。同样地，状态${\boldsymbol{E}}_{i2}^r$在有限时间$T_{i2}^r$内收敛到零。可以得出估计子系统（37）是有限时间收敛的。

3.5   控制子系统稳定性分析

将式（17）代入式（16），可以得到动力学控制子系统的误差动态：

由引理3和引理4可知，微分器估计误差$\tilde{\alpha}_{iU}^{\mathrm{d}},\tilde{\alpha}_{ir}^{\mathrm{d}}$和超螺旋观测器估计误差${\tilde \sigma _{iU}}$, ${\tilde \sigma _{ir}}$在$t > \max \left\{ {T_{i1}^U,T_{i1}^r,T_{i2}^U,T_{i2}^r} \right\}$时收敛到零。因此，将$\tilde{\alpha}_{iU}^{\mathrm{d}}=0$，$\tilde{\alpha}_{ir}^{\mathrm{d}}=0$，${\tilde \sigma _{iU}} = 0$和${\tilde \sigma _{ir}} = 0$代入式（42）中，可得

定义$\boldsymbol{E}_{i 3}^U=\left[\left\lceil z_{i U}\right\rfloor^{\tfrac{1}{2}}, \eta_{i U}\right]^{\mathrm{T}}, \;\boldsymbol{E}_{i 3}^r=\left[\left\lceil z_{i r}\right\rfloor^{\tfrac{1}{2}}, \eta_{i r}\right]^{\mathrm{T}}$, $\varsigma _{iU}^z{\text{ = }} {\left| {{z_{iU}}} \right|^{ - \tfrac{1}{2}}},\varsigma _{ir}^z{\text{ = }}{\left| {{z_{ir}}} \right|^{ - \tfrac{1}{2}}}$，则式（43）可写成向量形式：

其中：

注意到子系统${\boldsymbol{E}}_{i3}^U$和${\boldsymbol{E}}_{i3}^r$有相同的形式，在此以子系统${\boldsymbol{E}}_{i3}^U$为例给出详细分析。

引理5：若存在正定对称矩阵${\boldsymbol{P}}_{i3}^U,{\boldsymbol{Q}}_{i3}^U \in {{\bf{R}}^{2 \times 2}}$使等式$\boldsymbol{A}_{i3}^{U\mathrm{T}}\boldsymbol{P}_{i3}^U+\boldsymbol{P}_{i3}^U\boldsymbol{A}_{i3}^U=-\boldsymbol{Q}_{i3}^U$成立。则超螺旋动力学控制子系统${\boldsymbol{E}}_{i3}^U$，以${\mu _{iU}}$为输入，以${\boldsymbol{E}}_{i3}^U$为状态，是有限时间收敛的。

证明：构建李雅普诺夫函数：

利用式（44），对$V_{i3}^U$求时间的导数，可得

将不等式$\varsigma _{iU}^z\left\| {{\boldsymbol{E}}_{i3}^U} \right\| > 1$代入（46），可得

因为式（45）为二次正定函数，故有${\lambda _{\min }}\left( {{\boldsymbol{P}}_{i3}^U} \right){\left\| {{\boldsymbol{E}}_{i3}^U} \right\|^2} \leqslant V_{i3}^U \leqslant {\lambda _{\max }}\left( {{\boldsymbol{P}}_{i3}^U} \right){\left\| {{\boldsymbol{E}}_{i3}^U} \right\|^2}$，由此可得$\left\| {{\boldsymbol{E}}_{i3}^U} \right\| \geqslant \sqrt {{{V_{i3}^U} \mathord{\left/ {\vphantom {{V_{i3}^U} {{\lambda _{\max }}}}} \right. } {{\lambda _{\max }}}}\left( {{\boldsymbol{P}}_{i3}^U} \right)}$。将所得不等式继续代入式（47），可得

因此，状态${\boldsymbol{E}}_{i3}^U$在有限时间$T_{i3}^U \leqslant 2{\sqrt {{\lambda _{\max }}\left( {{\boldsymbol{P}}_{i3}^U} \right)} }/ {{\lambda _{\min }}}\left( {{\boldsymbol{Q}}_{i3}^U} \right)V_{i3}^{U\tfrac{1}{2}}\left( {\max \left\{ {T_{i1}^U,T_{i2}^U} \right\}} \right)$内收敛到零。同样地，状态${\boldsymbol{E}}_{i3}^r$在有限时间$T_{i3}^r$内收敛到0。可以得出超螺旋动力学控制子系统式（44）有限时间收敛。

3.6   闭环系统稳定性分析

最后给出整个系统的稳定性分析。将协同子系统式（20），制导子系统式（28），非线性微分器子系统式（35），估计子系统式（37），和控制子系统式（44）所组成的系统看作一个输入为$h=[\boldsymbol{\varsigma}_{\theta}^{\mathrm{T}},\boldsymbol{h}_i^{\mathrm{T}},\mu_{iU},\mu_{ir}]^{\mathrm{T}}$，状态为$E=[\boldsymbol{\theta}_e^{\mathrm{T}},\boldsymbol{E}_{i1}^{\mathrm{T}},\boldsymbol{E}_{i2}^{U\mathrm{T}},\boldsymbol{E}_{i2}^{r\mathrm{T}}, \boldsymbol{E}_{i3}^{U\mathrm{T}},\boldsymbol{E}_{i3}^{r\mathrm{T}}]^{\mathrm{T}}$的级联系统$\varPi$。所组成的闭环级联系统的稳定性由定理1给出。

定理1：在满足假设1的前提下，考虑无人船动态式（1）和式（2），路径参数预估器式（7），动态事件触发机制式（9），动态事件触发路径参数更新律式（8），运动学制导律式（12），非线性微分器式（13），超螺旋观测器式（15），超螺旋的动力学控制律式（17），使得组成的闭环级联系统$\varPi$是输入−状态稳定的。

证明：根据引理1～引理5，可得闭环级联系统$\varPi$，以h为输入，以E为状态，是输入−状态稳定的。存在$\mathcal{K}\mathcal{L}$类函数$\gamma$和$\mathcal{K}$类函数$\kappa$，使得系统状态满足：

系统输入h有界，可以得到闭环系统内所有误差信号E都是一致最终有界的。

3.7   芝诺分析

定理2：采用所提动态事件触发机制式（9），控制系统不会发生芝诺现象，即触发间隔有正下界。

证明：对测量误差${\varsigma _{i\theta }}$在区间$t \in [t_k^i,t_{k + 1}^i)$求时间的导数，可得

式中，${\hbar _{i\theta }} \in {{\bf{R}}^ + }$为上界。

根据事件触发原理，当有事件被触发时，测量误差被重置为零，即${\varsigma _{i\theta }}(t_k^i) = 0$。对式（49）在区间$t \in [t_k^i,t_{k + 1}^i)$积分，可得

根据动态事件触发机制式（9），可知$\varsigma_{i\theta}^2-\xi_{i\theta}^2\theta_{i\mathrm{c}}^2- \varepsilon_{i\theta}\leqslant\eta_{i\theta}$成立。将其代入${\dot \eta _{i\theta }}$可得${\dot \eta _{i\theta }} \geqslant - {\rho _{i\eta }}{\eta _{i\theta }} - {\eta _{i\theta }}$。那么有$\eta_{i\theta}\ge\eta_{i\theta}(0)\mathrm{e}^{-(\rho_{i\eta}+1)t}＞0$。

根据动态事件触发机制式（9），当$t \to t_{k + 1}^i$时，测量误差${\varsigma _{i\theta }}$满足

式中，${\varepsilon }_{i\theta }\in {{\bf{R}}}^{+}$为下界。

联合式（50）和式（51）可得相邻触发间隔的下界满足

因此，采用所提动态事件触发机制式（9），系统不会发生芝诺现象。

4.   仿真结果

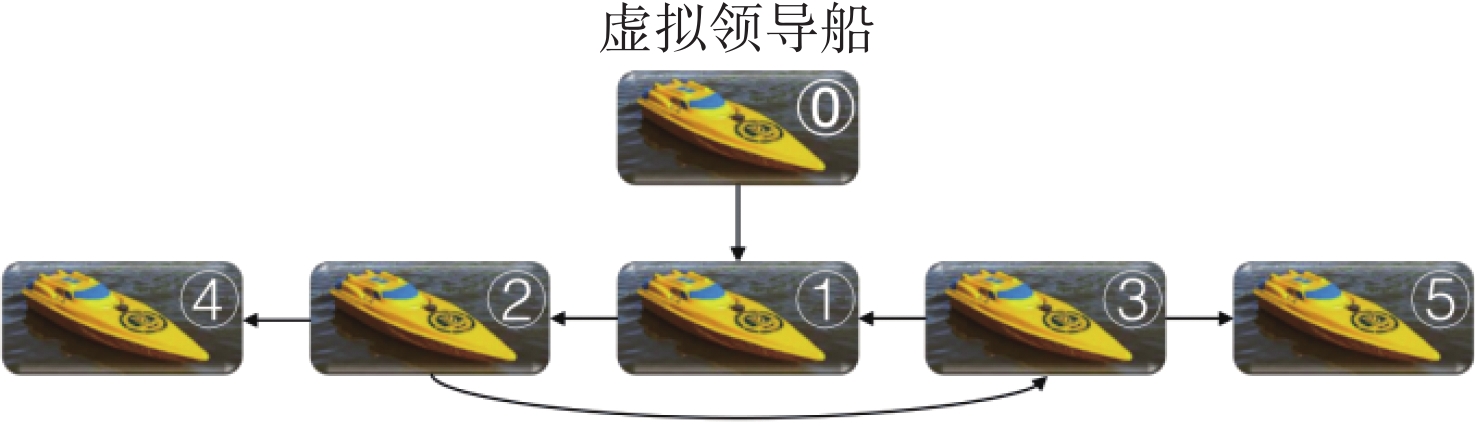
考虑由一个虚拟领导船和5艘无人船组成的系统，其中的无人船模型参考文献[25]中的参数。无人船之间的通信拓扑如图3所示。控制参数设为${v_0} = 0.3,\;k_{i1}^\theta = 0.3,\;k_{i2}^\theta = 1.5$，${k_{i1}} = {\text{0}}{\text{.2}},\;{k_{i2}} = {\text{0}}{\text{.3}}$，$\mathit{\Delta}_{i1}=\text{1}$，$\mathit{\Delta}_{i2}=\text{1}$，$\mathit{\Delta}_{i3} = 8$，$\rho _{i1}^U = {\text{1}},\;\rho _{i2}^U = {\text{0}}{\text{.1}},\;\rho _{i1}^r = {\text{1}}$，$\rho _{i2}^r = {\text{0}}{\text{.1}}$，$k_{i1}^U = {\text{60}}$, $k_{i2}^U = {\text{50}}$, $k_{i1}^r = {\text{20}}$, $k_{i2}^r = {\text{20}}$，$k_{i1}^{\mathrm{c}u}=\text{20}, k_{i2}^{\mathrm{c}u} = 0.1,\; k_{i1}^{\mathrm{c}u}=\text{40}$，$k_{i2}^{\mathrm{c}r}=0.1$，${\xi _{i\theta }} = {\text{0}}{\text{.01}}$，$\eta_{i\theta}(0)=\text{0}\text{.001}, \rho_{i\eta}=0.08,\; \varepsilon_{i\theta}=0.000\ 1$。为了说明所提动态事件触发方法的有效性，将所提动态事件触发机制式（9）与Praveen等^[18]研究中的静态事件触发机制进行比较，并选取相同的触发参数。

图  3  通信拓扑

Figure  3.  The communication topology

下载: 全尺寸图片 幻灯片

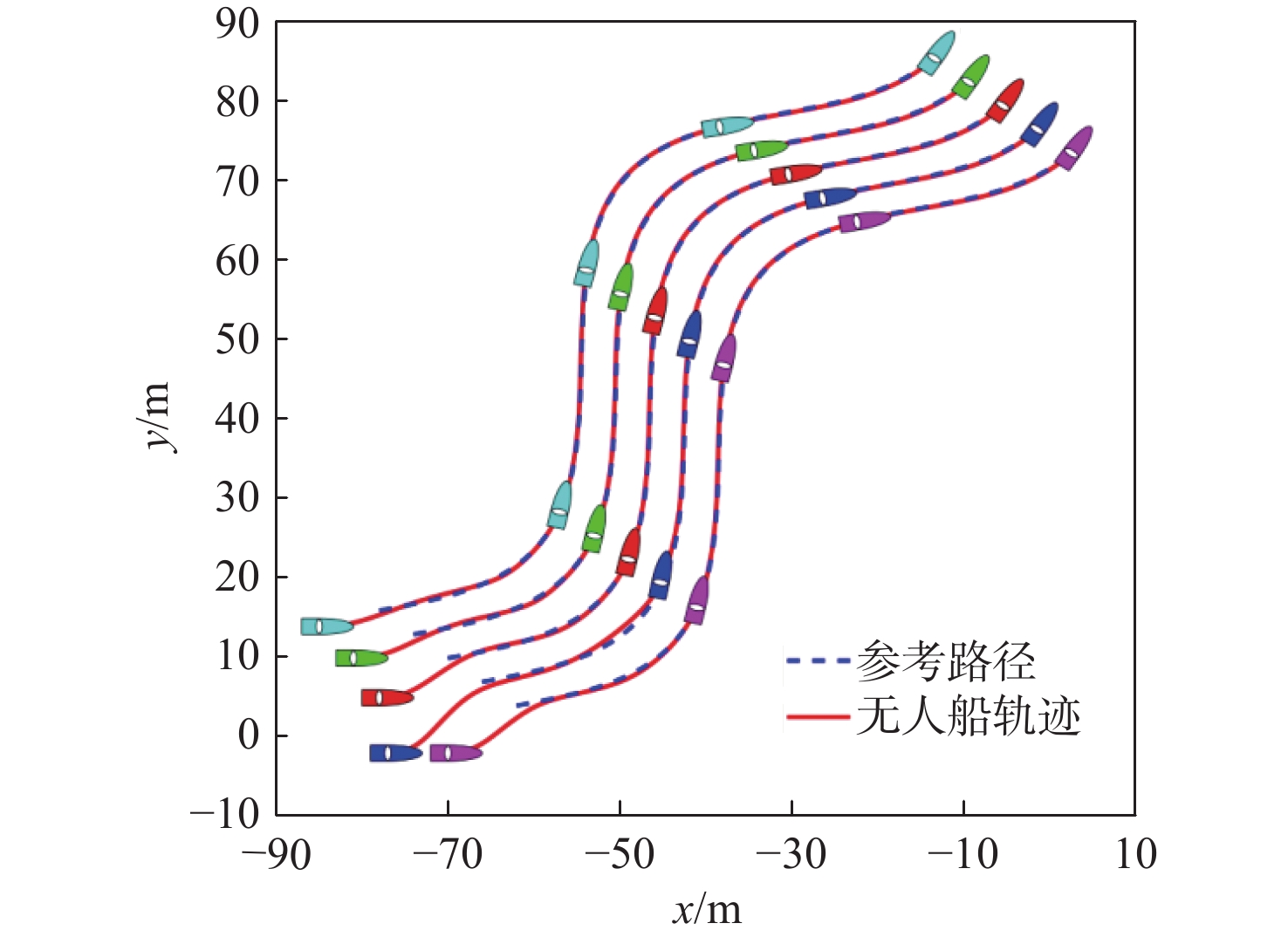
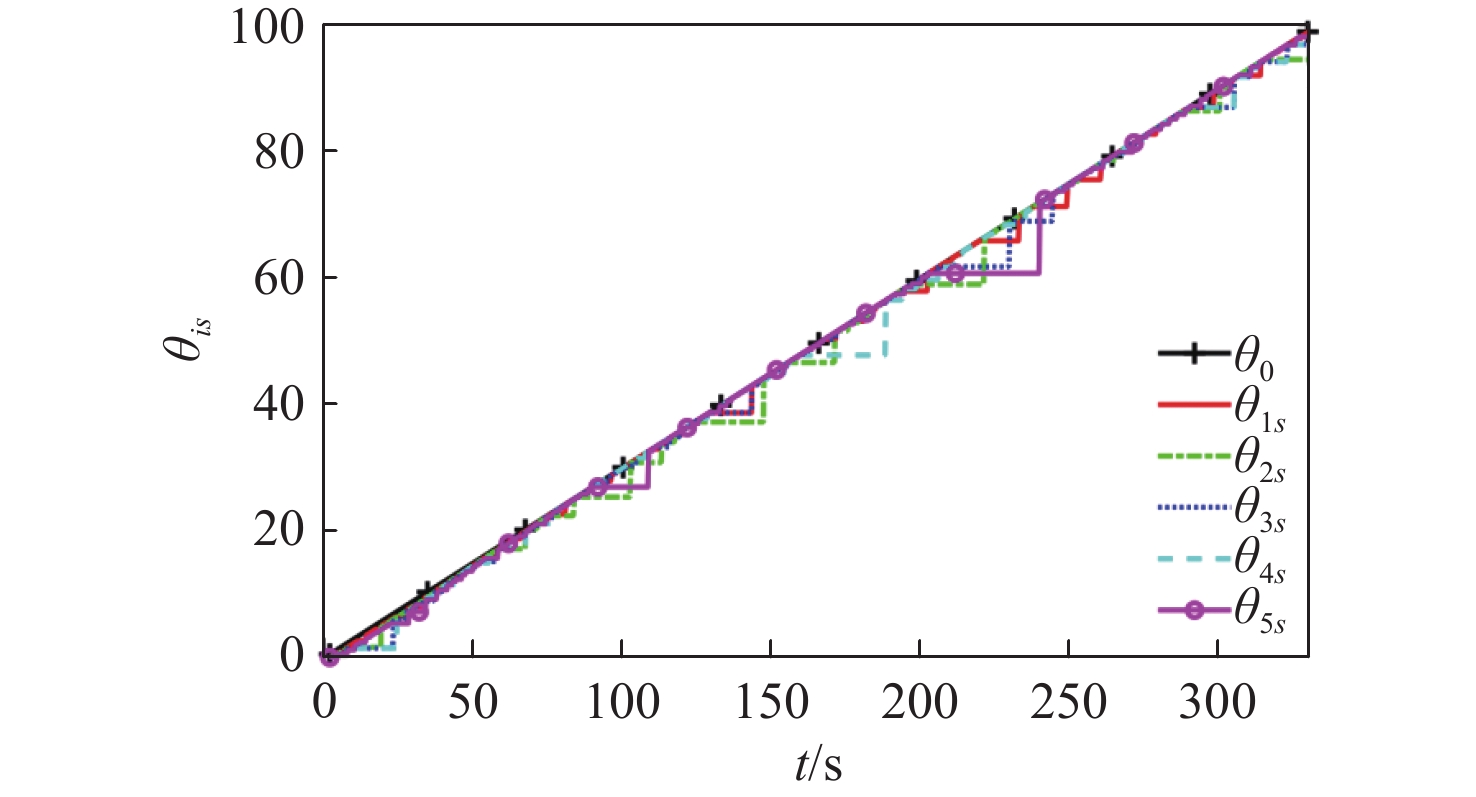
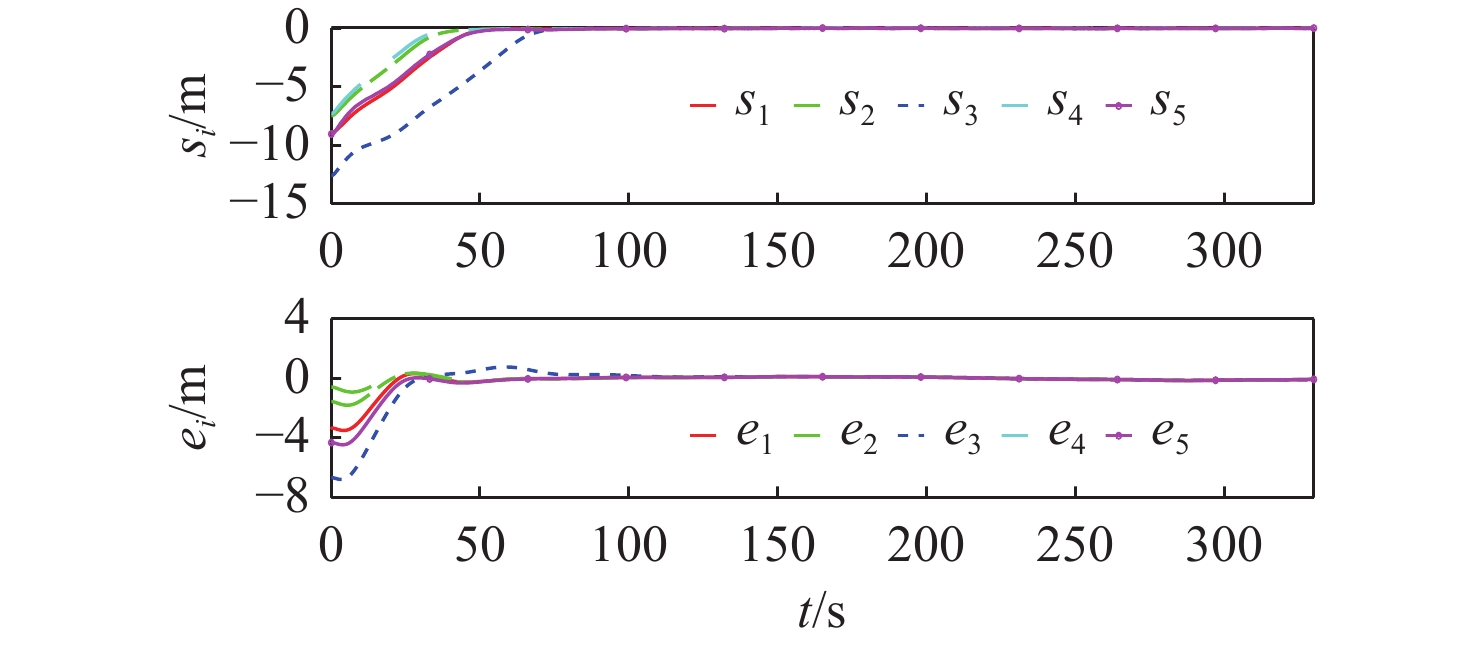
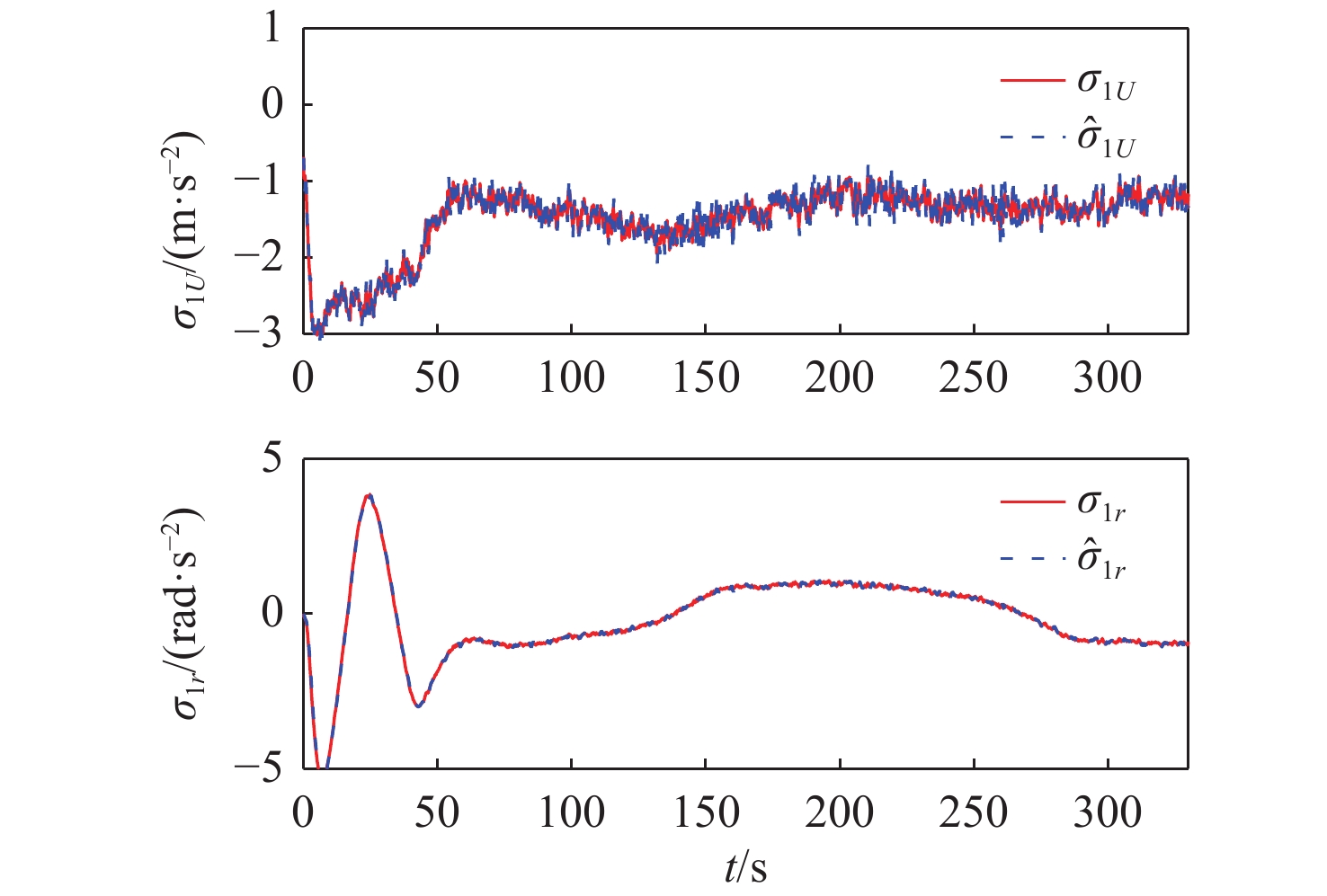
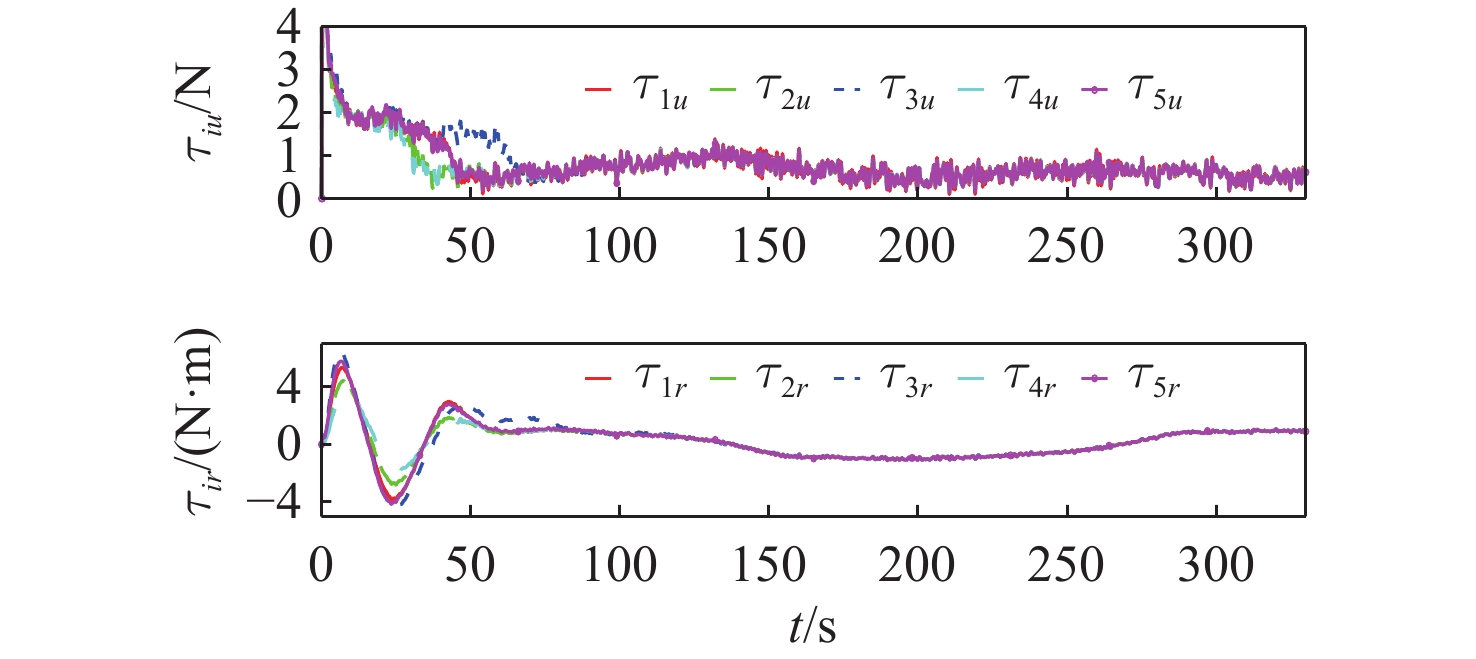
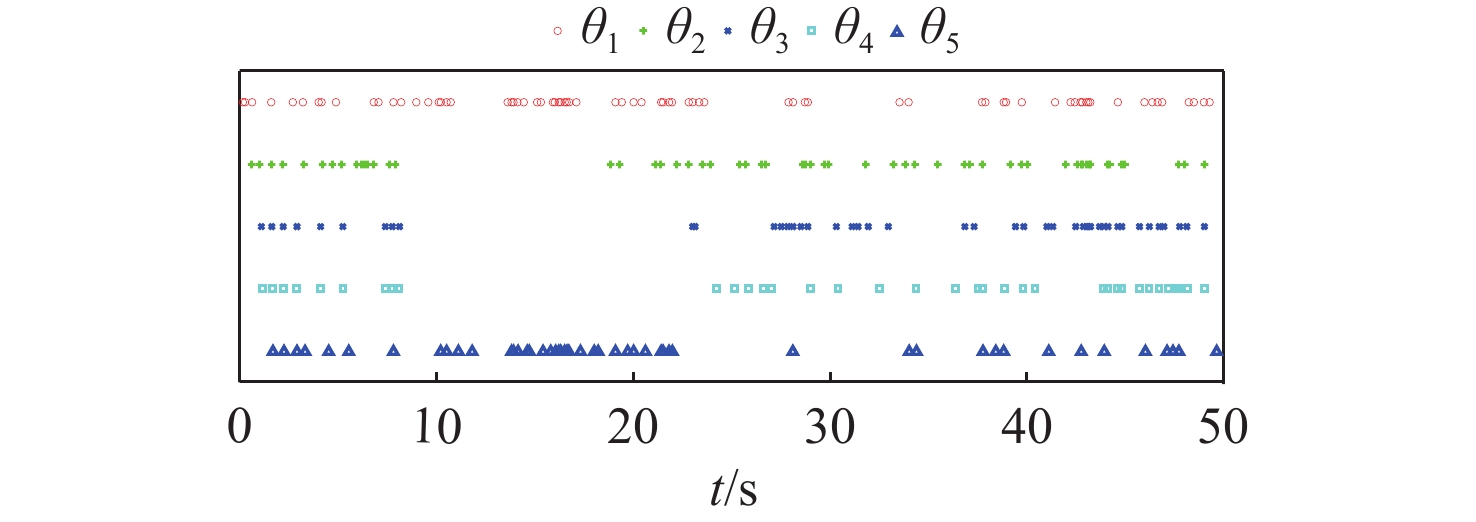
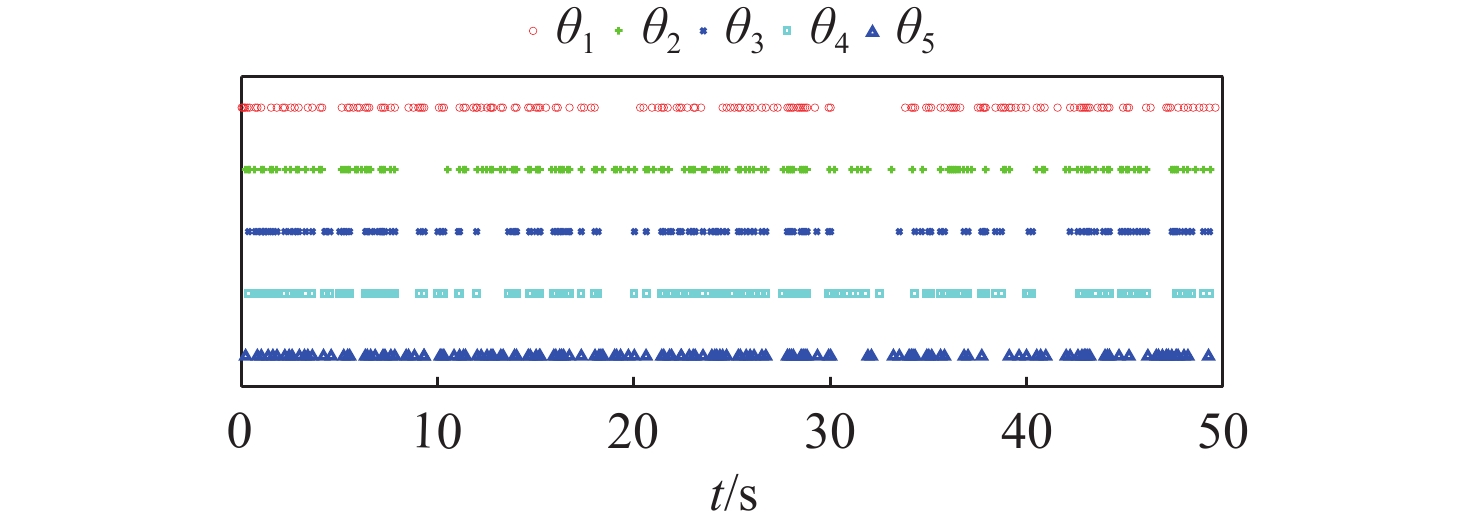
仿真结果如图4～图10所示。图4给出了5艘无人船的运动轨迹，从图中可以看出，采用所提动态事件触发无人船协同路径跟踪控制方法，可以实现并排编队任务。图5为路径参数的演化情况，可以看出5艘无人船的路径参数和虚拟领导船的路径参数趋于一致，实现了协同任务。图6为路径跟踪中的横向和纵向跟踪误差，可以看出跟踪误差收敛到原点的邻域内。图7为1号无人船超螺旋观测器对总扰动的估计效果，可以看出所提超螺旋观测器能够对总扰动进行准确估计。图8为5艘无人船的控制输入。图9和图10分别为采用所提动态事件触发机制和采用Praveen等^[18]研究中的静态事件触发机制时，结合5艘无人船通信触发的事件，可以看出采用本章所提的动态事件触发机制，且采用相同事件触发的参数，在稳态时发生更少的触发事件。表1在330 s的仿真中，分别采用所提动态事件触发机制（DET）、静态事件触发机制（SET）和时间触发机制（TT，触发间隔0.01 s）时，5艘无人船的触发次数。从总的触发占比可以看出：采用静态事件触发机制相比于时间触发可以减少96.87%的网络占用；采用动态事件触发机制相比于时间触发可以减少98.83%的网络占用；采用所提动态事件触发机制比静态事件触发机制占用更少的网络通信带宽资源。

图  4  所提动态事件触发无人船协同路径跟踪控制效果

Figure  4.  The cooperative path following performance of the proposed dynamic event-triggered cooperative path following control method

下载: 全尺寸图片 幻灯片

图  5  路径参数的演化

Figure  5.  The evolution of the path variables

下载: 全尺寸图片 幻灯片

图  6  横向和纵向跟踪误差

Figure  6.  The along-track errors and the cross-track errors

下载: 全尺寸图片 幻灯片

图  7  超螺旋观测器对总扰动的估计效果

Figure  7.  The disturbances estimated by the proposed STO

下载: 全尺寸图片 幻灯片

图  8  无人船的控制输入

Figure  8.  The control inputs of the USVs

下载: 全尺寸图片 幻灯片

图  9  动态事件触发机制下触发的事件

Figure  9.  The communication events by using the proposed dynamic event-trigger mechanism

下载: 全尺寸图片 幻灯片

图  10  静态事件触发机制下触发的事件

Figure  10.  The communication events by using the proposed static event-trigger mechanism

下载: 全尺寸图片 幻灯片

表  1  不同方法的触发次数

Table  1.  Triggering times by using different mechanisms

	触发次数				触发占比/%
	DET	SET	TT		DET	SET
无人船1	506	1 101	33 000		1.533	3.336
无人船2	309	1 003	33 000		0.936	3.039
无人船3	351	1 017	33 000		1.064	3.082
无人船4	357	1 040	33 000		1.082	3.152
无人船5	402	998	33 000		1.218	3.024
总次数	1925	5 159	165 000		1.167	3.127

下载: 导出CSV 

| 显示表格

5.   结　语

本文主要研究了网络带宽资源受限、模型参数不确定和环境扰动情况下的多无人船协同路径跟踪控制问题，提出了基于动态事件触发的多无人船协同路径跟踪控制方法。所提控制方法包括非周期通信的动态事件触发路径参数更新律、基于LOS的制导律、有限时间收敛的非线性微分器、有限时间收敛的超螺旋观测器和有限时间收敛的超螺旋动力学控制律。采用所提控制方法，多无人船可以在完成协同路径跟踪任务的同时，降低网络通信量。通过级联稳定性理论分析，证明了协同路径跟踪闭环系统是输入–状态稳定的，所有误差信号一致最终有界。芝诺分析证明了所提动态事件触发机制不存在芝诺现象。对比仿真结果验证所提控制方法的有效性。在后续研究工作中，将进一步考虑部分特殊工况下的协同路径跟踪控制问题。