0.   引　言

随着全球能源危机与环境恶化问题的加剧，发展低碳航运技术已成为船舶工业转型的必然选择^[1]。转筒帆船（rotor-assisted vehicle，RAV）能够利用转筒帆产生的马格努斯效应进行高效推进，兼具结构简单、安装灵活与环境适应性强等特点，已成为近海工程与远洋运输领域的研究热点^[2-4]。然而，帆−舵-桨的联合控制机理对船舶路径跟踪控制提出了巨大挑战，因此，研究融合了转筒速率调节机制的帆式船舶制导与控制一体化算法，对推动绿色船舶发展具有重要的理论价值与实际意义。

制导与控制这2大子系统是决定船舶路径跟踪性能的关键因素^[5]。其中，制导系统主要负责路径解算与期望运动指令的生成，而控制系统则通过驱动执行机构实现动态误差的抑制。在制导系统设计中，视线导航法（line-of-sight，LOS）及其改进算法（如积分型ILOS^[6]、自适应ALOS^[7]）因结构简洁目前已被广泛应用于船舶与无人机领域。Zhang等^[8]提出了一种逻辑虚拟船（logical virtual ship，LVS）制导算法，通过构建虚拟船提前规划并生成光滑的参考路径，可解决传统LOS制导在转向阶段容易出现超调现象的问题。在此基础上，Li等^[9]进一步提出了干预LVS制导算法，即通过引入饱和补偿函数来缓解执行器输入饱和的问题。然而，上述制导算法均需持续解算制导信号并实时传输至控制系统，导致通信信道负载过高，在复杂海况下还有可能引发数据丢包及系统失稳等潜在的风险。

在控制系统设计中，当船舶面临复杂多变的外部环境或频繁的任务切换时，传统连续控制策略往往会导致控制指令高频更新，从而引发信道带宽占用加剧、计算负担加重以及执行器磨损等一系列问题^[10-12]。事件触发控制（event-triggered control，ETC）是通过预设阈值条件来实现控制指令的间歇性更新，可为解决上述问题提供有效的途径。李纪强等^[13]提出一种混合阈值ETC策略，通过静态/动态阈值参数的灵活调节，在系统通信效率与跟踪精度之间实现了动态平衡。吕旻高等^[14]设计了基于事件触发机制的路径参数预估器，通过对路径参数的间接更新，有效降低了多无人船协同网络的通信负载。Zhang等^[15]提出了一种多端口ETC策略，该策略仅在满足触发条件时同步更新误差反馈信号和控制输入，显著降低了系统资源消耗。但值得注意的是，现有的触发机制普遍基于状态波动幅度设计阈值，当系统受持续低频扰动影响时，状态误差变化缓慢，容易因为未达到触发阈值而导致信号更新滞后，造成控制精度下降，尤其是在狭窄的水道或是港口等需要精准控制的场景中，这种滞后可能引发航迹偏移，威胁船舶航行安全。

基于以上分析，本文将以牛顿−拉格朗日非线性数学模型为控制对象，通过融合转筒帆转速调节机制，提出一种鲁棒自适应ETC算法。首先，结合现有的虚拟制导算法设计一种基于有限边界的干预LVS制导律，在兼顾输入饱和的基础上引入有限边界圆规则，有效降低制导信号的传输频率，从而避免通信冗余问题；然后，针对传统的事件触发机制在低频扰动下响应滞后的问题，提出一种耦合鲁棒神经阻尼、动态面控制和积分事件触发的自适应控制算法，用以提高船舶自主航行安全与能源利用效率。

1.   模型描述

在本文中，$\left| \cdot \right|$表示绝对值，${\left\| \cdot \right\|}$表示Euclidean范数，${\hat {( \cdot )}}$表示$( \cdot )$的估计值，并且${\widetilde {( \cdot )} = \hat {( \cdot )} - ( \cdot )}$。

1.1   转筒帆船的数学模型

基于经典Fossen欠驱动船舶数学模型^[16]，考虑到实际的海洋环境干扰，建立适用于帆式船舶的牛顿−拉格朗日非线性数学模型如式（1）所示。

式中：${\boldsymbol{\eta}} = {\left[ {x,y,\psi } \right]^{\rm{T}}}$，为船舶位置坐标和艏向信号；${\boldsymbol{\nu }} = {\left[ {u,v,r} \right]^{\rm{T}}}$，为船舶前进速度、横漂速度和转艏角速度；${m}_{u}，{m}_{v}$，${m_r}$为船体附加质量；${f}_{u}\left({\boldsymbol{\nu}} \right)，{f}_{v}\left({\boldsymbol{\nu}} \right)$，${f_r}\left( {\boldsymbol{\nu }} \right)$为模型结构未知项；${d}_{\text{w}u}，{d}_{\text{w}v}$和${d_{{\text{w}}r}}$为外界海洋环境干扰力；${\tau _{\text{p}}} = {T_u}\left( \cdot \right)\left| n \right|n$，${\tau _{\text{r}}} = {F_r}\left( \cdot \right)\delta$，分别为由螺旋桨和舵产生的前进推力与转艏力矩，其中${T_u}\left( \cdot \right)$和${F_r}\left( \cdot \right)$为执行器增益函数，n和$\delta$分别为主机转速与舵角；${\tau _{\text{s}}}$为转筒帆产生的辅助推进力。

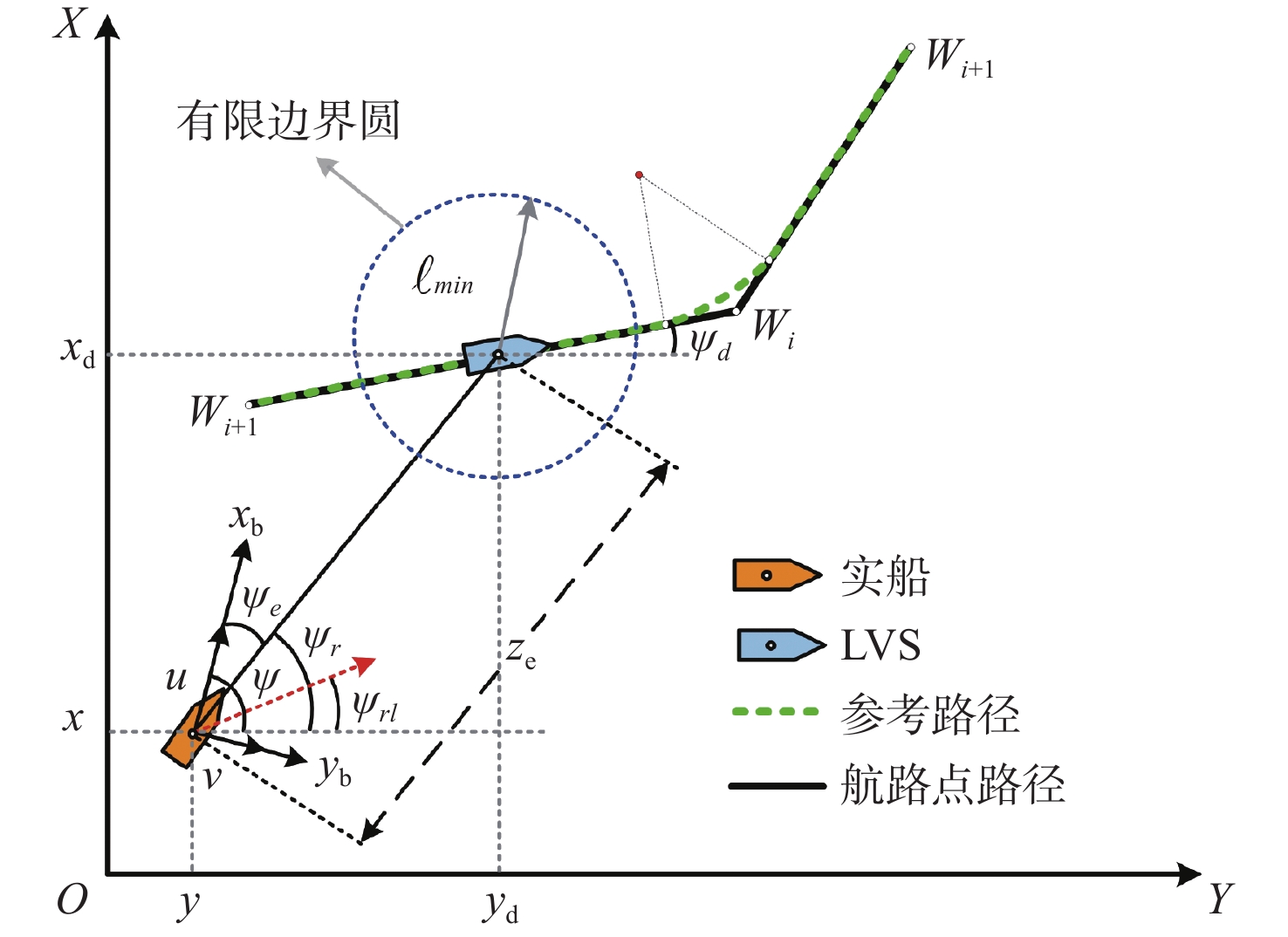
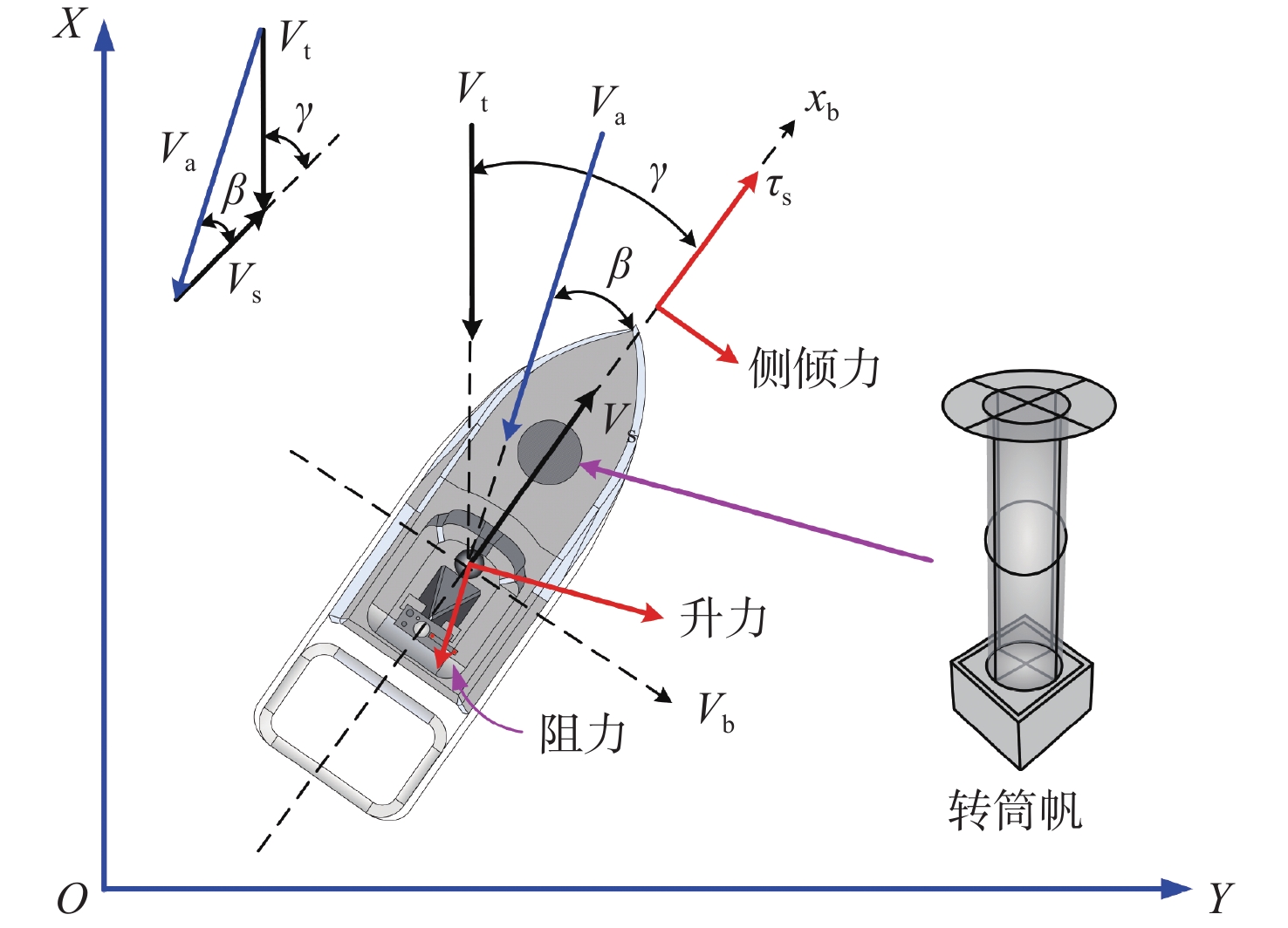
转筒帆的受力分析如图1所示。图中：X，Y轴对应大地坐标系，分别指向正北和正东；${x_{\text{b}}}$，${y_{\text{b}}}$轴对应船舶附体坐标系，分别指向船首艏和右舷；${V_{\text{s}}}$表示船速；${V_{\text{t}}}$，$\gamma$分别为真风速度和真风向与船艏向的夹角；${V_{\text{a}}}$，$\beta$分别为视风速度和视风向与船艏向的夹角，具体表达式如式（2）所示。

图  1  转筒帆受力分析图

Figure  1.  Force analysis diagram of the rotor-sail

下载: 全尺寸图片 幻灯片

转筒帆的辅助推力可以表示为

式中：${\rho _{\boldsymbol{A}}}$为空气密度；A为转筒帆的最大投影面积；${C_{\text{L}}}$为升力系数，${C_{\text{D}}}$为阻力系数，其计算公式可参考文献[17]，其核心参数旋转比（spin ratio, SR）定义为$SR = {\text{π}}d{n_{\text{s}}}/60{V_{\text{a}}}$，其中${n_{\text{s}}}$为转筒帆转速。需注意，文献[17]所提公式仅适用于转筒直径d为上端板直径${d_{\text{e}}}$的一半且展弦比为6的转筒帆。

在海洋工程实践中，转筒帆船通常需要根据海上实时风况动态调整转筒速率和旋转方向，从而实现最优能效。因此，本文设计了以下基于实时风场感知的转筒速率调节机制：

式中：${\bar n_{\text{s}}}$为转筒最大转速；${k_{\text{s}}}$为与转筒材料和电机效率等相关的经验系数。

为增强控制器设计的严谨性，提出以下假设：

假设1：对于外界海洋环境扰动${d_{{\text{w}}u}}$，${d_{{\text{w}}v}}$和${d_{{\text{w}}r}}$存在未知上界${\overline{d}}_{\text{w}u}，{\overline{d}}_{\text{w}v}，{\overline{d}}_{\text{w}r}$，满足$\left|{d}_{\text{w}u}\right|\le {\overline{d}}_{\text{w}u}， \left|{d}_{\text{w}v}\right|\le {\overline{d}}_{\text{w}v}，\left|{d}_{\text{w}r}\right|\le {\overline{d}}_{\text{w}r}$。

假设2：船舶横漂速度被动有界稳定^[18]。

假设3：期望航向${\psi _{\text{d}}}$二阶可导。

1.2   径向基函数神经网络

引理1：结合连续分离函数技术，对于任意定义在紧集${\Omega _{ {\boldsymbol{x}}}} \subset {\mathbb{R}^m}$上的连续函数$f\left( {\boldsymbol{x}} \right)(f(0) = 0)$，均可采用径向基函数（RBF）神经网络以任意精度逼近^[19]，即

式中：$\varepsilon \left( {\boldsymbol{x}} \right)$为存在上界$\bar \varepsilon \left( {\boldsymbol{x}} \right)$的近似误差；${\boldsymbol{S}}\left( {\boldsymbol{x}} \right) = \left[ {{s_1}\left( {\boldsymbol{x}} \right),{s_2}\left( {\boldsymbol{x}} \right), \cdots ,{s_l}\left( {\boldsymbol{x}} \right)} \right]$，为式（6）所示的高斯函数，其中$l > 1$为神经网络节点数。

式中，${\mu _i}$和${\phi _i}$分别为高斯函数的中心与宽度值。m为状态矢量${\boldsymbol{x}}$的维数，则权重矩阵${\boldsymbol{A}}$可以表示为

2.   基于有限边界的干预制导

为避免转向超调问题，本文利用LVS，根据预设的航路点（Waypoint）信息${W_1}\left( {{x_1},{y_1}} \right),$ ${W_2}\left( {{x_2},{y_2}} \right), \cdots , {W_n}\left( {{x_n},{y_n}} \right)$生成平滑参考路径，如式（8）所示。设计的制导原理框架如图2所示。

图  2  基于有限边界的干预LVS制导

Figure  2.  Intervened LVS guidance based on finite boundary

下载: 全尺寸图片 幻灯片

式中：${{\boldsymbol{\eta }}_{\text{d}}} = {\left[ {{x_{\text{d}}},{y_{\text{d}}},{\psi _{\text{d}}}} \right]^{\text{T}}}$，为LVS的位置坐标和艏向信号；${u_{\text{d}}}$，${r_{\text{d}}}$分别为LVS的期望前进速度和转艏角速度。根据实船与LVS的位置关系，制导律可初步推导为式（9）。

式中：${x}_{\text{e}}={x}_{\text{d}}-x；{y}_{\text{e}}={y}_{\text{d}}-y；{{\textit{z}}}_{\text{e}}=\sqrt{{x}_{\text{e}}^{2}+{y}_{\text{e}}^{\text{2}}}$。

进一步地，引入有限边界圆触发规则。当船舶进入边界圆覆盖区域，即满足触发条件${{\textit{z}}_{\text{e}}} \leqslant {\ell _{\min }}$时，制导信号将停止更新，以此降低通信负载，如式（10）所示。有限边界圆的半径${\ell _{\min }}$需根据船长、船舶操纵性能和跟踪精度需求等因素进行合理选择。

最后，设计式（11）所示的饱和补偿函数，将舵角约束嵌入制导律中，以缓解执行器输入饱和问题。

式中：${\psi }_{\text{e}}={\psi }_{\text{r}\iota }-\psi ；\iota =\mathrm{tanh}\left(\delta \text{/}{\delta }_{\text{sat}}\right)$，其中$\delta$为舵角，${\delta _{{\text{sat}}}}$为饱和舵角。

3.   控制器设计与稳定性分析

3.1   事件触发控制器设计

步骤1：分别对位置误差${{\textit{z}}_{\text{e}}}$和艏向误差${\psi _{\text{e}}}$求导，得式（12）。

式中，${{\textit{z}}_{\Delta }} = {\dot x_{\text{d}}}\cos \left( {{\psi _{{\text{r}}\iota }}} \right) + {\dot y_{\text{d}}}\sin \left( {{\psi _{{\text{r}}\iota }}} \right) - v\sin \left( {{\psi _{\text{e}}}} \right)$。

为了镇定上述跟踪误差，设计如下虚拟控制律${\alpha _u}$和${\alpha _r}$，其中${k}_{{\textit{z}}}，{k}_{\psi }$为正参数。

针对传统反步法在虚拟控制律设计中需进行多次微分导致的“计算复杂性爆炸”问题，引入动态面控制（dynamic surface control，DSC）技术。

式中：$i=u，r$；${\vartheta _i}$为大于0的时间参数；${\alpha _i}$为虚拟控制律；${\beta _i}$为动态面信号。${d_i}$为滤波误差，其表达式（15）如下，其中${B_i}( \cdot )$为有界函数。

步骤2：定义动态误差${u}_{\text{e}}={\beta }_{u}-u，{r}_{\text{e}}={\beta }_{r}-r$并对其求导，可得

根据引理1，采用RBF神经网络在线逼近模型未知项${f_u}\left( {\boldsymbol{\nu }} \right)$和${f_r}\left( {\boldsymbol{\nu }} \right)$，如式（17）所示。

令${b}_{i}={\Vert {\boldsymbol{A}}_{i}\Vert }_{\text{F}}，{\boldsymbol{A}}_{i}^{m}={\boldsymbol{A}}_{i}/{\Vert {\boldsymbol{A}}_{i}\Vert }_{\text{F}}，{\omega }_{i}={\boldsymbol{A}}_{i}^{m}{i}_{\text{e}}$，其中$i=u，r$，进一步可以转换为${b_i}{\omega _i} = {{\boldsymbol{A}}_i}{i_{\text{e}}}$。为简化控制器设计，构造鲁棒神经阻尼项${\eta _i}$，消除模型不确定性和环境干扰项。

式中：${\varphi }_{i}=1+\Vert {S}_{i}\Vert ；{\theta }_{i}=\mathrm{max}\{\Vert {\boldsymbol{A}}_{i}{\beta }_{i}\Vert ，{\overline{\varepsilon }}_{i}+{\overline{d}}_{\text{w}i}\}$。

对于复杂海况下的转筒帆船，持续调整转筒速率不可避免地会导致船舶主机和舵机控制输入$n，\delta$的频繁变化。因此，本文设计了一种基于累计误差的积分事件触发机制，其核心设计如下。

当且仅当满足式（20）的事件触发条件时，控制命令才会更新，否则，保持不变。

式中：${e}_{u}={n}_{u}\left({t}_{u}\right)-{n}_{k}^{u}\left({t}_{k}^{u}\right)；{e}_{r}=\delta \left({t}_{r}\right)-{\delta }_{k}^{r}\left({t}_{k}^{r}\right)$；${\varpi _i},{\varsigma _i},i = u,r$，为正的触发阈值参数。

通过结合自适应技术，对系统增益不确定性进行在线补偿，令${\lambda _u} = {1 \mathord{\left/ {\vphantom {1 {{T_u}\left( \cdot \right)}}} \right. } {{T_u}\left( \cdot \right)}},{\lambda _r} = {1 \mathord{\left/ {\vphantom {1 {{F_r}\left( \cdot \right)}}} \right. } {{F_r}\left( \cdot \right)}},$则$N\text{=}\left|{n}_{k}^{u}\right|{n}_{k}^{u}={\hat{\lambda }}_{u}{\alpha }_{N}，{\delta }_{k}^{r}={\hat{\lambda }}_{r}{\alpha }_{\delta }$。其中，${\alpha _N}$和${\alpha _\delta }$为直接控制律，如式（21）所示，相应的自适应律如式（22）所示。

式中：${\varPhi _i} = {{\left( {\varphi _i^2 + {\boldsymbol{S}}{{\left( {\boldsymbol{\nu }} \right)}^{\text{T}}}{\boldsymbol{S}}\left( {\boldsymbol{\nu }} \right)} \right)}/ 4}$，其中$i=u，r$；${k_u},{k_r}, {k_{u{\text{e}}}},{k_{r{\text{e}}}},{\chi _u},{\chi _r},{\gamma _u},{\gamma _r}$为人为设定的正参数；定义自适应误差为${\tilde{\lambda }}_{u}={\hat{\lambda }}_{u}-{\lambda }_{u}，{\tilde{\lambda }}_{r}={\hat{\lambda }}_{r}-{\lambda }_{r}$。

3.2   系统稳定性分析

定理1：基于转筒帆船模型（式（1）～式（4）），在满足假设1～假设3的条件下，采用虚拟控制律（式（13））、动态面技术（式（14））、积分事件触发规则（式（19）～式（20））、控制律（式（21））和自适应律（式（22）），可以保证闭环控制系统中的所有误差变量满足半全局一致最终有界（semi-global uniform and ultimately bounded，SGUUB），并且通过合理调节设计参数，可以使跟踪误差收敛至零点附近的任意小邻域内。

证明：构造Lyapunov候选函数V。

对V进行求导，可得

为了对式（24）进行放缩处理，引入杨氏不等式（式（25）～式（27）），其中${c_i}$为正参数。

结合控制律（式（21））和自适应律（式（22）），$\dot V$最终可简化为式（28）。

其中：

定义$\kappa = \min \left\{ {{k_{\textit{z}}} - 1,{k_\psi } - 1,{\kappa _{di}},{\kappa _i},{\gamma _i}\chi _i^{ - 1}} \right\},2D ={T_u}\left( \cdot \right)$ ${\gamma _u}{\left( {{\lambda _u} - {{\hat \lambda }_u}\left( 0 \right)} \right)^2} + {F_r}\left( \cdot \right){\gamma _r}{\left( {{\lambda _r} - {{\hat \lambda }_r}\left( 0 \right)} \right)^2} + {c_u} + {c_r} +$ $\theta _u^2/{k_{u{\text{e}}}} + \theta _r^2/{k_{r{\text{e}}}}$，则式（28）可进一步表示为

分别对两端进行积分运算，可得

式中：$V(t)$有界且满足$\mathop {\lim }\limits_{t \to \infty } V(t) \leqslant D/2\kappa$。因此，本文所设计控制器中所有的误差信号均满足SGUUB收敛，定理1得证。

4.   仿真实验

为了验证所提控制算法的有效性和优越性，本文选取文献[20]中提出的算法作为对比算法，基于NORSOK风谱和JONSWAP波谱对4级海况下的海洋环境予以了模拟^[10]，风速10 m/s，风向180°。在相同初始条件下，采用三自由度的转筒帆船（船长38 m，船宽6.8 m，质量118 000 kg，转筒高度18 m，转筒直径3 m）作为被控对象，进行MATLAB数值仿真实验。在本节仿真实验中，船舶的路径跟踪控制建立在转筒风帆转速调节机制之上，即优先考虑风帆助航的节能效率。实验仿真步长设置为0.01 s，船舶初始航向为0°，主要设计参数如表1所示。

表  1  主要设计参数

Table  1.  Main design parameters

参数	数值		参数	数值
${k_{\textit{z}}}$	$1.2$		${\chi _r}$	$0.1$
${k_\psi }$	$10$		${\gamma _u}$	$0.8$
${k_u}$	$3.5$		${\gamma _r}$	$1.2$
${k_r}$	$1.3$		${\vartheta _i}$	$0.1$
${k_{u{\text{e}}}}$	$3.0$		${\varpi _u}$	$3.0$
${k_{r{\text{e}}}}$	$3.0$		${\varpi _r}$	$2 5$
${\chi _u}$	$0.05$		${\varsigma _i}$	$5.0$

下载: 导出CSV 

| 显示表格

在系统仿真过程中，参数的选取主要依赖于经验指导与试错机制相结合的方法。众所周知，较大的增益系数${k_{\textit{z}}},{k_\psi },{k_u},{k_r}$能够有效提高系统跟踪精度。然而，这种配置可能会引发控制信号幅值超限和系统抖动，导致控制资源的过度消耗。同时，较大的事件触发阈值参数${\varpi _u},{\varpi _r},{\varsigma _u},{\varsigma _r}$虽然能显著降低信号传输频率，却也可能造成控制精度的损失。因此，需要通过多次仿真实验进行有针对性的参数优化，进而在跟踪精度、能源效率和控制平滑度之间实现最佳平衡。

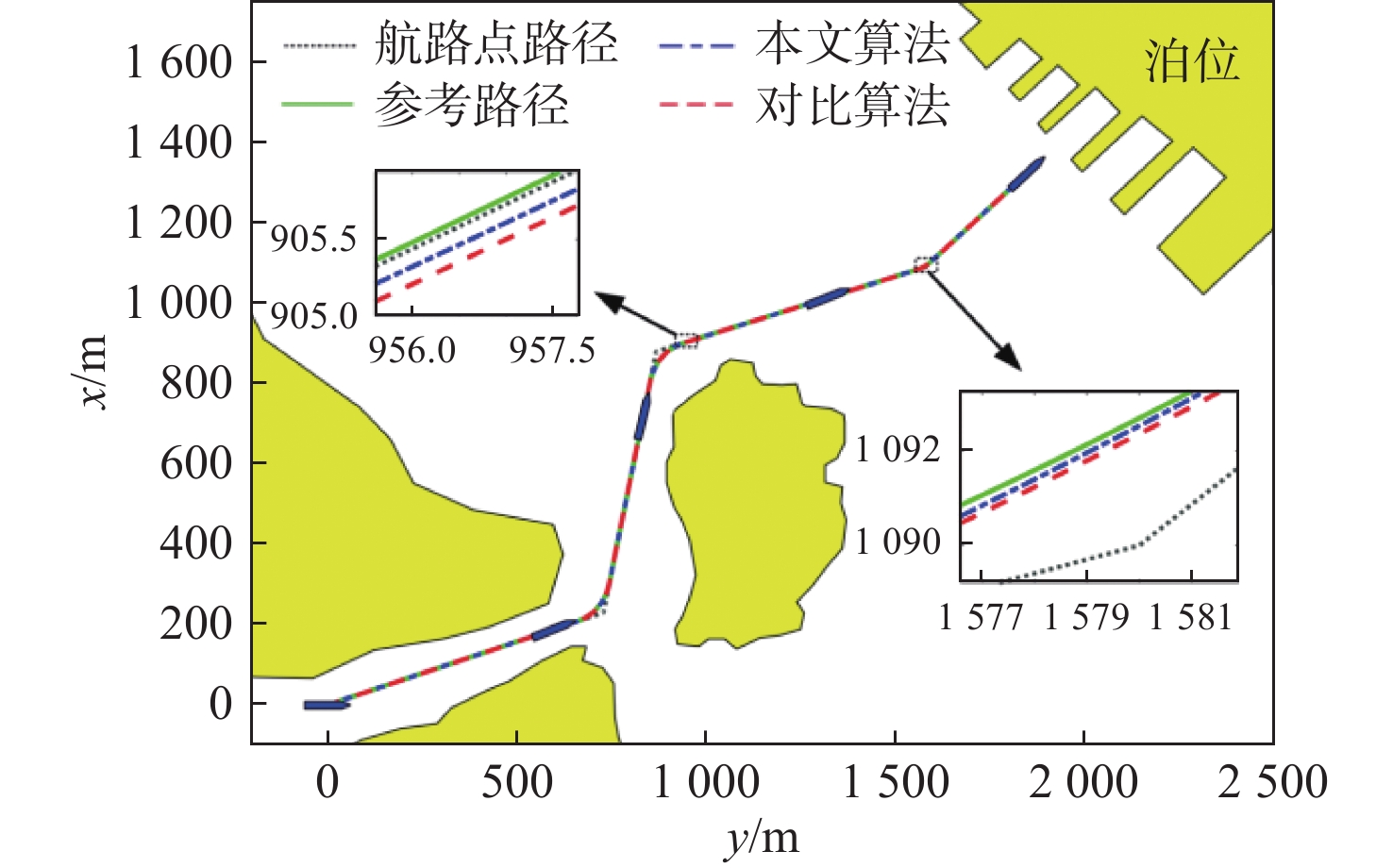
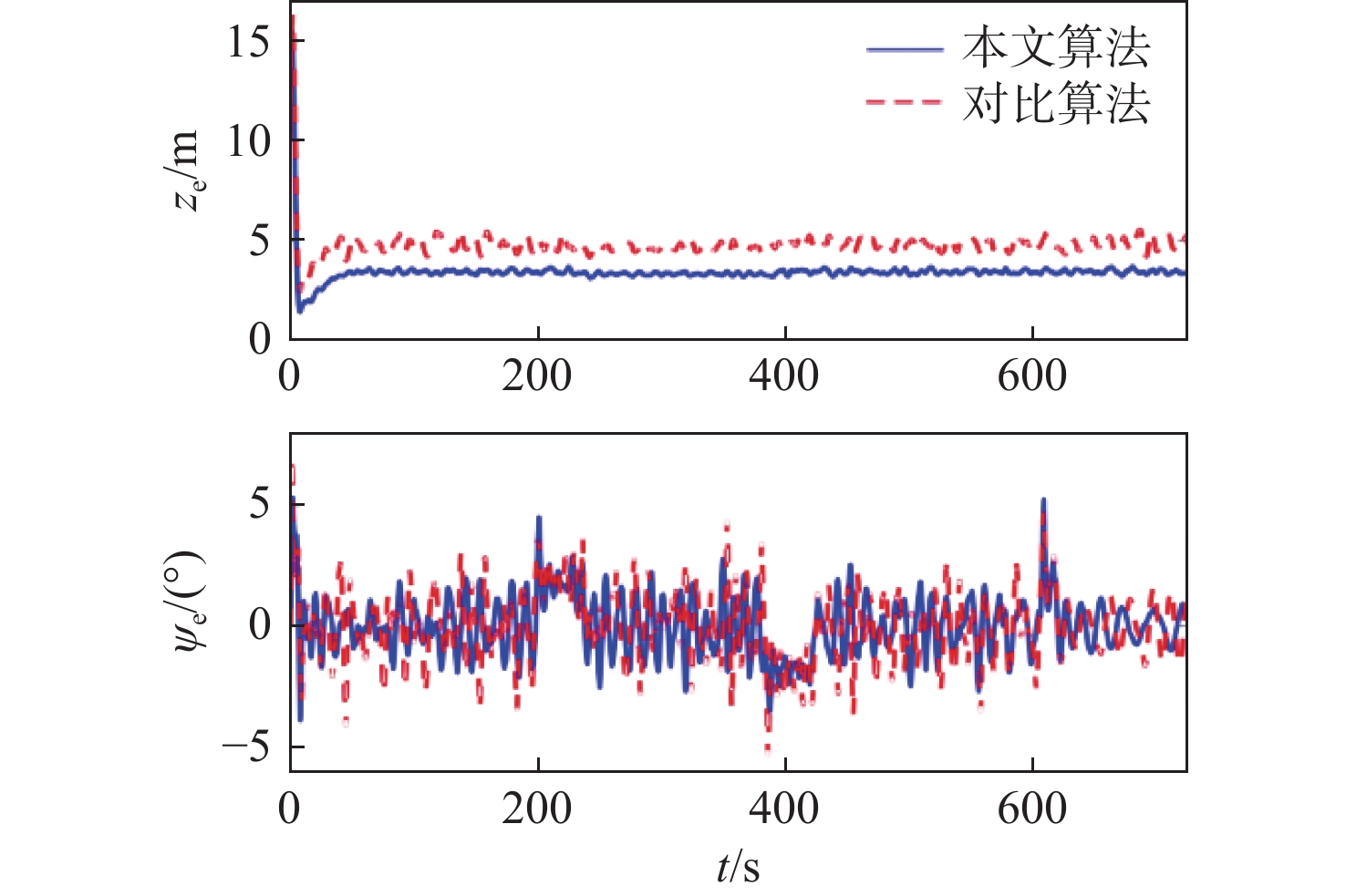
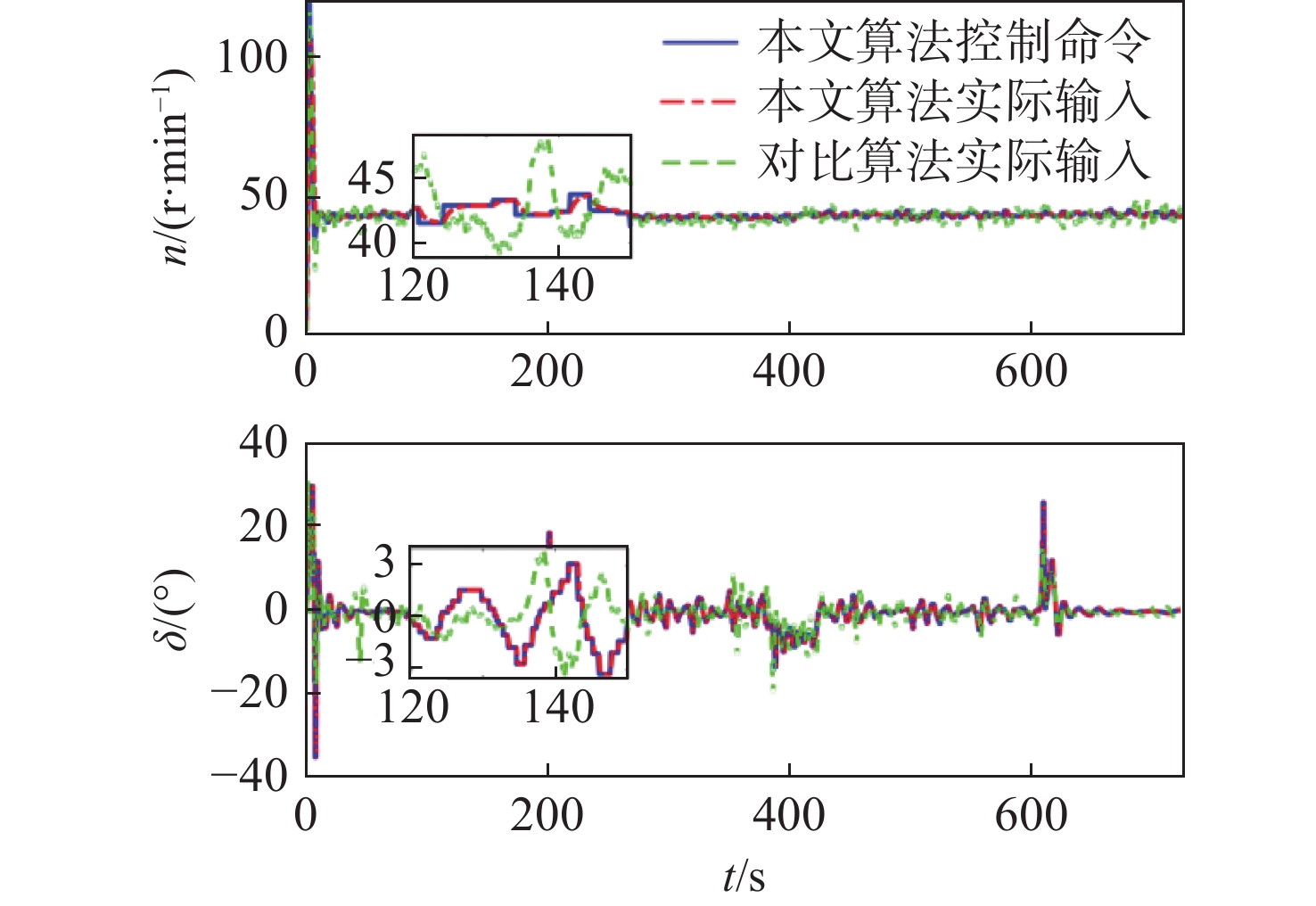
实验仿真结果如图3～图8所示。图3展示了转筒帆船在2种控制算法下的路径跟踪轨迹和局部轨迹放大图。图4为2种算法下船舶的跟踪误差曲线。由图可知，本文算法具备更高的控制精度以及更快的响应能力，能够将位置和艏向误差精准控制在$\pm$3 m和$\pm$5°范围内。图5描述了2种算法下的控制输入曲线。值得注意的是，由于事件触发机制和伺服系统的引入，本文算法的控制输入均处于执行器动作允许范围内，且信号抖振明显下降，有效减少了执行器的机械磨损，能为船舶长期稳定运行提供有力的保障。

图  3  船舶跟踪轨迹曲线

Figure  3.  Ship tracking trajectory curves

下载: 全尺寸图片 幻灯片

图  4  路径跟踪误差曲线

Figure  4.  Path following error curves

下载: 全尺寸图片 幻灯片

图  5  控制输入曲线

Figure  5.  Control input curves

下载: 全尺寸图片 幻灯片

图  6  事件触发采样间隔

Figure  6.  Time interval of the event-triggered sampling points

下载: 全尺寸图片 幻灯片

图  7  自适应参数曲线

Figure  7.  Adaptive parameter curves

下载: 全尺寸图片 幻灯片

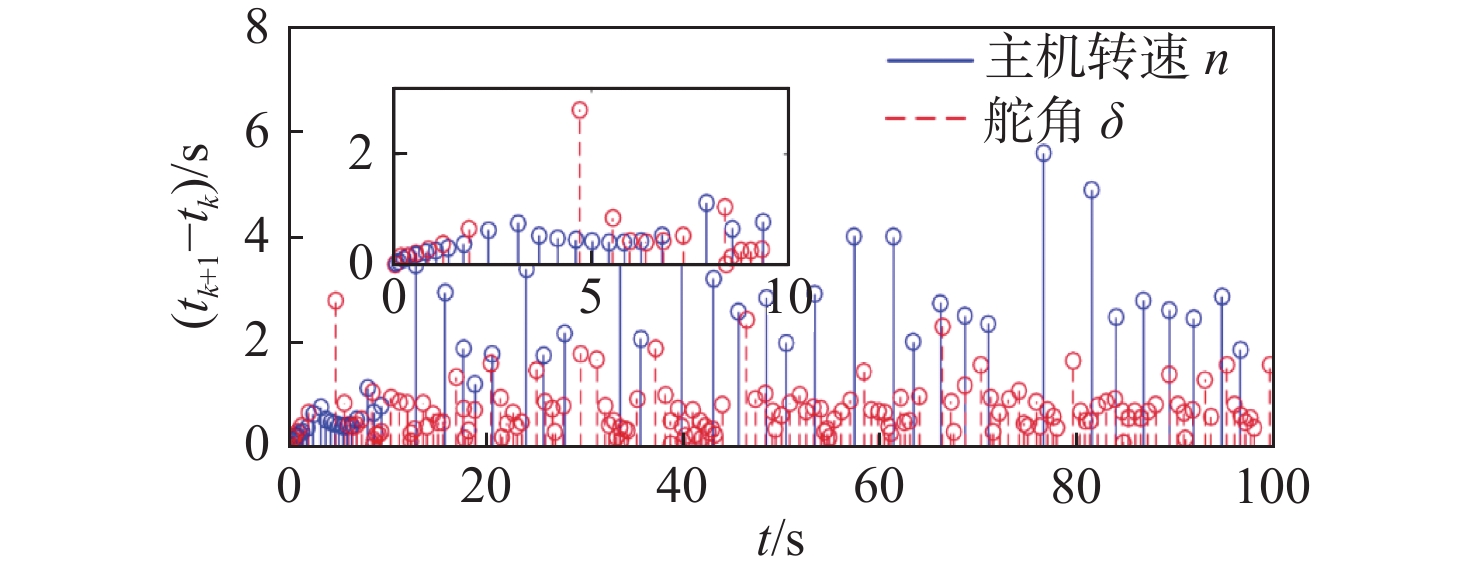
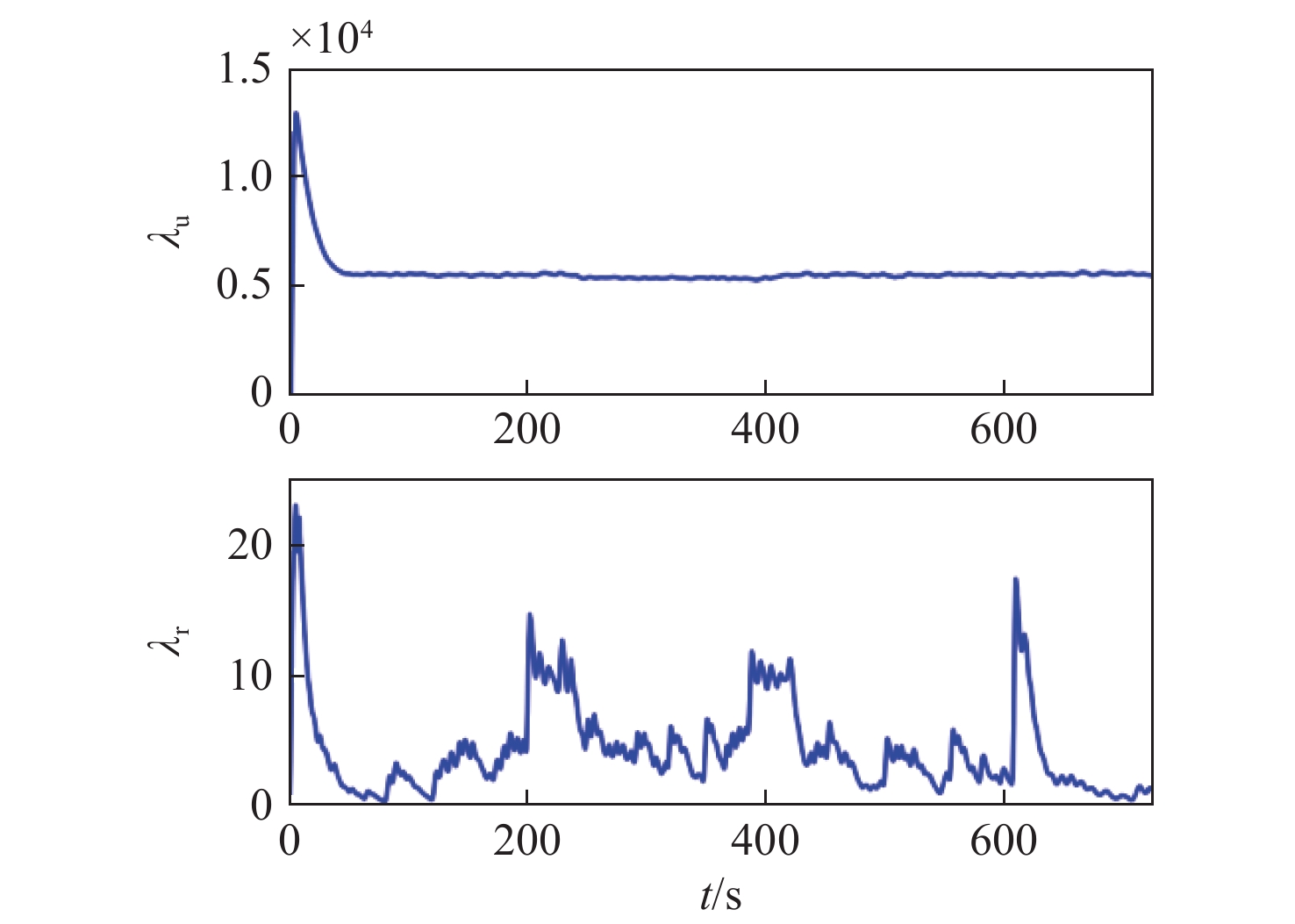
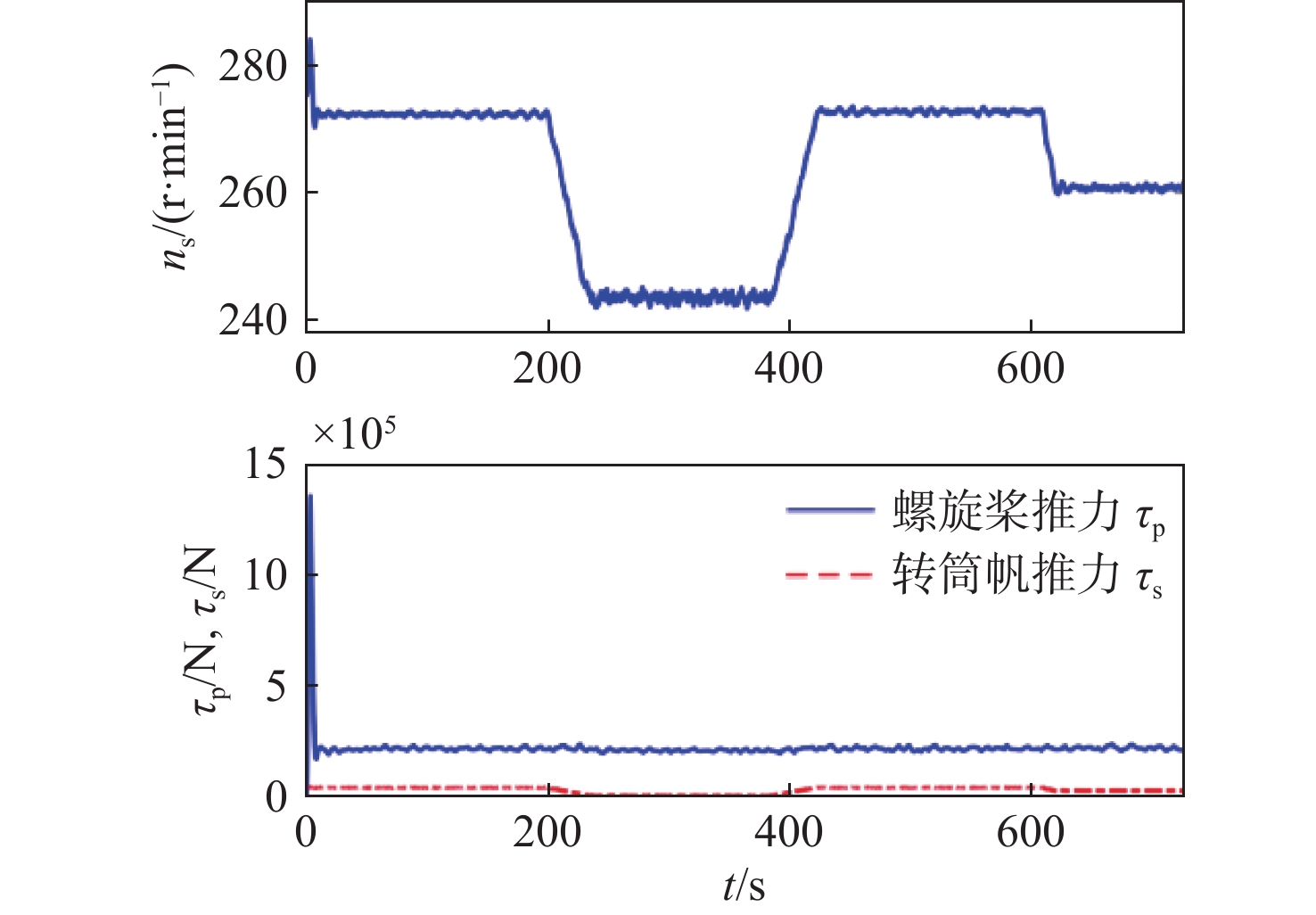
图6所示为本文算法在0～100 s时的事件触发采样间隔示意图。图7所示为控制器自适应参数曲线，由图可见所设计的自适应律能够有效收敛。图8呈现了本文算法下转筒帆的转速及其螺旋桨推力${\tau _{\text{p}}}$与转筒帆推力${\tau _{\text{s}}}$之间的对比曲线。航程能耗节省（energy consumption saving，ECS）可通过${\text{ECS}} = {\tau _{\text{s}}}/({\tau _{\text{p}}} + {\tau _{\text{s}}})$计算。结果显示，采用转筒风帆助航策略能够节省约11.6%的能源消耗，这对推动航运业朝绿色、可持续方向转型具有重要意义。

图  8  转筒速率及船舶前进推力

Figure  8.  Rotor rate and ship forward thrust

下载: 全尺寸图片 幻灯片

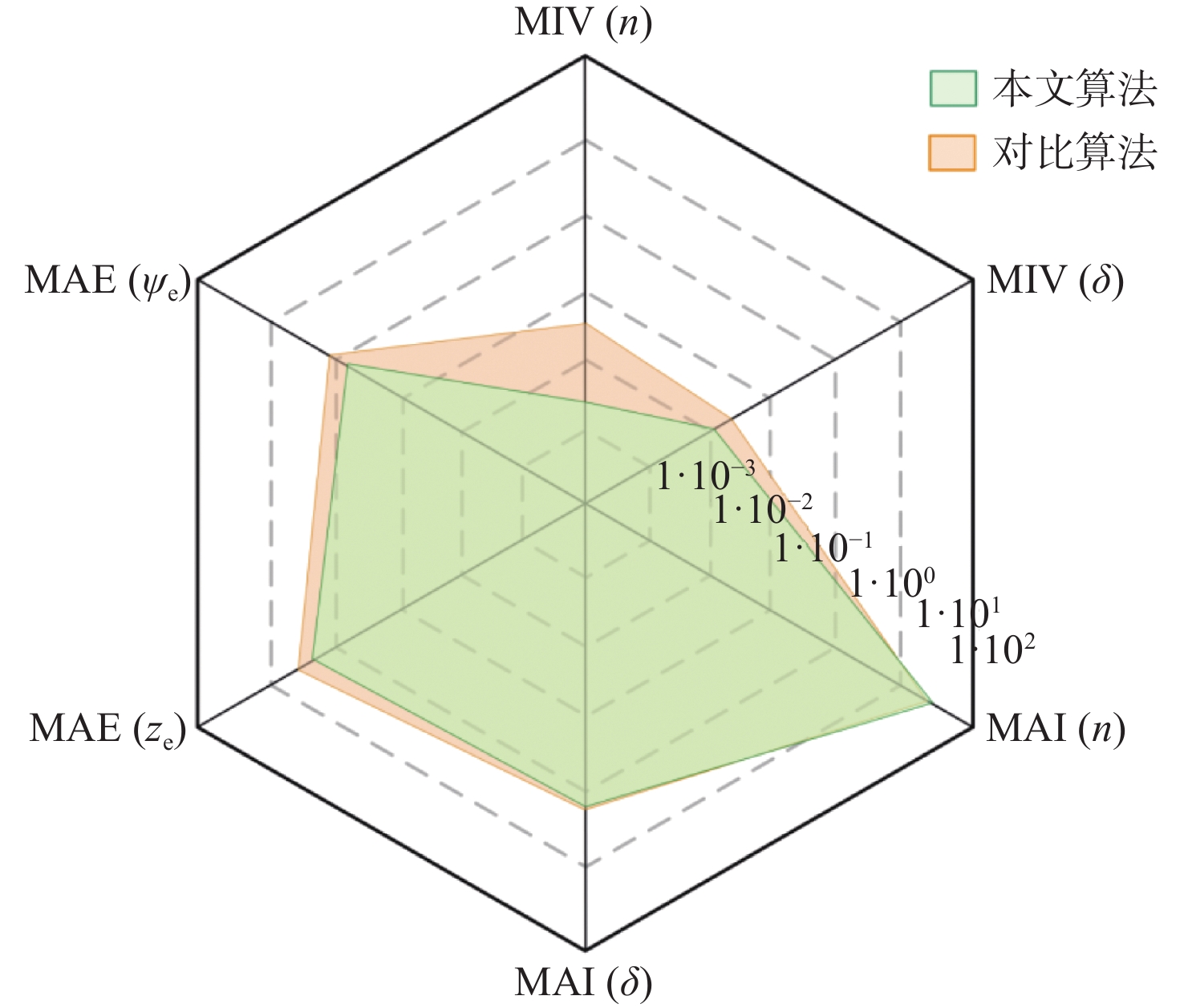
为定量分析本文算法控制性能的优势，选取了3个具有代表性的指标^[5]，即平均绝对控制误差（MAE）、平均绝对控制输入（MAI）和平均控制输入变差（MIV），这3个指标分别用于精度评估、能耗评估和执行器寿命评估。图9展示了2种控制算法量化指标的对比雷达图。由图可见，除了MAI的数值相近外，本文算法的MAE和MIV指标均明显低于对比算法，这就意味着本文算法具有更高的控制精度和更长的执行器寿命，与前文的分析结果一致。

图  9  对比雷达图

Figure  9.  Comparative radar charts

下载: 全尺寸图片 幻灯片

5.   结　语

本文针对考虑转筒速率调节的转筒帆船路径跟踪控制问题，提出了一种结合改进干预LVS制导律与积分事件触发机制的鲁棒自适应控制算法，该算法通过引入有限边界圆规则，显著降低了制导系统的通信负载，并通过饱和补偿函数抑制了舵机输入饱和现象，提升了系统稳定性。此外，所设计的积分事件触发控制算法在维持跟踪精度（位置误差≤3 m，艏向偏差≤5°）的前提下，能显著降低控制命令的传输频率，有效缓解了执行器的机械磨损与工作强度。仿真实验表明，在4级海况下，所提风帆助航策略可实现11.6%的推进系统能效提升，对推动低碳航运技术发展具有重要的工程应用价值。

未来，可通过集成机器学习与强化学习等智能算法，实现海洋环境参数的在线辨识与动态趋势预测，从而提前调整船舶控制策略与转筒帆转速参数，进一步提升船舶在复杂海况下的航行性能与节能效果。