0.   引　言

在舰艇艏部“导流罩−声呐腔−声呐舱背板耦合结构”中，声呐舱背板作为连接声呐系统与艇体结构的关键界面，其力学参数对机械激励响应的控制具有重要影响。航行器在水下航行时，由螺旋桨、主机等设备产生的宽频振动会通过艇体结构传递至导流罩及声呐腔，而背板是振动能量传递的重要通道。若背板刚度不足，可能会引发局部共振，导致声呐换能器阵列的指向性畸变和信号失真；而阻尼特性缺失则会加剧振动能量的积累，通过声振耦合效应产生二次噪声，显著降低声呐系统的信噪比。通过数值仿真研究背板参数的敏感性，可抑制振动传递路径，在保障结构强度的同时提升声呐探测精度与舰艇声隐身性能。

由于实际的导流罩罩体结构为三维复杂壳体结构，难以建立其理论模型，而且导流罩流激响应分析主要集中在罩体表面湍流边界层充分发展区域，因此，在研究导流罩受湍流脉动压力激励下的自噪声时，国内外学者通常将矩形加筋平板视为实际导流罩的子单元，其理论模型为双侧触水。张成^[1]借鉴文献[2]中采用展开级数作为加筋平板的位移试函数，将复杂边界约束视为人工虚拟弹簧约束，研究了复杂边界约束下加筋平板的流激振动响应。孙亮明等^[3]基于层合理论建立声屏障夹芯板的分层计算模型，推导了简谐载荷作用下声屏障夹芯板的振动方程，获得了结构均方振速，求解了声屏障夹芯板的辐射声功率。俞孟萨等^[4]通过分析夹芯结构透声窗的声学性能，提出了一种新型的声学设计方法，分析了夹芯式透声窗的声传播特性，探讨了不同材料、结构参数对声学性能的影响，并优化了设计参数，以实现更好的声学性能。之前有学者在进行有限大平板水下流激振动响应预报时，假设平板结构嵌在无限大的刚性障板上，且平板两侧的声场为互不连通的半无限域，而实际的导流罩外侧声场近似为半无限域，内侧声场为有限空间的声腔。针对板−腔耦合结构研究，Du等^[5]和Kong等^[6]采用改进的傅里叶级数作为有限空间内部的声压试函数，将声腔的声压与薄板的位移函数耦合进行求解，得出了较为精确的背腔−板结构声振耦合结果。王鸿超^[7]利用有限元方法（FEM）分析了弹性板与声腔在不同边界条件下的耦合振动，探讨了边界条件对系统声振特性的影响，并提出了相应的减振降噪方法。彭彬彬等^[8]通过对矩形板及其背腔的声振特性进行分析，研究了不同参数对声振耦合效果的影响，研究结果表明，背腔的存在对矩形板的声振特性具有显著影响。孙小娟等^[9]基于Rayleigh-Ritz能量法和声振耦合理论，建立了弹性板结构和矩形声场的声振耦合模型，随后基于薄板理论，采用能量法推导弹性板的运动方程，得到了反映其固有属性的模态特征。裴雅真^[10]研究了加筋薄板结构和封闭声腔耦合系统的声振特性，其通过Rayleigh-Ritz能量法、模态叠加法和有限元方法，对矩形薄板、加筋板以及与矩形封闭声腔的耦合系统进行建模并予以了分析。刘进等^[11]通过建立传递矩阵模型，分析了薄壳腔体在随机激励作用下的声学响应，提出了一种有效的内部噪声预报方法。张成^[12]基于Layerwise理论建立夹芯板结构动力学模型，耦合结构振动与有限封闭声腔及半无限声场，通过能量泛函推导响应函数，验证模型及计算方法的正确性，分析了夹芯板高频流激响应特性和声腔高度对耦合系统的影响。目前，有关夹心板−声腔−背板耦合系统的声振理论研究尚非常匮乏。

本文拟分别采用薄板理论和Layerwise理论建立矩形平板、阻尼板及夹芯板的动力学模型，采用改进的傅里叶级数作为板结构的位移试函数，借助人工边界弹簧模拟弹性边界约束。首先，将夹芯板、平板（阻尼板）与封闭声腔和半无限声场耦合，建立能够适应不同结构边界约束和声腔边界条件的水下夹芯板−声腔−平板（阻尼板）耦合模型，考虑背板受到的激励，提出耦合模型响应求解方法，然后，与有限元计算进行对比，验证本文所提模型和求解方法的正确性；最后，探讨背板阻尼层、背板厚度与刚度以及声腔高度对结构振动与声腔声压的影响，为声呐结构中背板及声呐腔的设计提供参考。

1.   理论分析

1.1   矩形薄板振动响应函数

根据Kirchhoff薄板假设^[12]，薄板在弯曲振动时其弯曲中面处各点仅有法向位移而无平行于中面的位移。对于非简支约束下的平板，采用由传统傅里叶级数与附加项组合而成的改进型傅里叶级数作为薄板弯曲振动位移试函数。附加项的表达形式多样^[13-15]，本文采用文献[15]中所提的级数，其具体表达式如下：

式中：a，b分别为薄板长和薄板宽；m，n为整数。

矩形薄板的弯曲振动位移函数可以写为

式中：x，y分别为平板在2个方向的坐标；M，N分别为位移试函数f_m(x)和g_n(y)的截断项数；${{\boldsymbol{A}}_{\rm{P}}}$为由待定系数${A_{\rm{P}}}_{mn}$依次组成的列向量；ζ为由f_m(x)和g_n(y)各项的乘积组成的列向量；ω为圆频率；t为时间。

根据薄板振动理论，薄板的弯曲应变能为

式中：$D = \widetilde E{h^3}/\left( {12\left( {1-{\mu ^2}} \right)} \right)$，为薄板单位宽度的弯曲刚度，其中h为平板厚度；平板材料的复弹性模量$\widetilde E = E(1 + \eta )$，其中E，$\eta$分别为材料的弹性模量和阻尼损耗因子；$\mu$为泊松比；${S_{\rm{p}}}$为薄板面积。

薄板的动能为

式中，${\rho _{\text{p}}}$为薄板密度。

为能简便地模拟各种边界条件对平板的约束，将边界约束视为沿着平板边界线均匀分布的人工虚拟弹簧约束，通过调整人工弹簧（包括位移弹簧和转角弹簧）的刚度值来实现对不同程度边界约束的模拟。对薄板结构而言，边界约束可以视为作用于薄板中面处的法向位移弹簧和边界切向转角弹簧。边界人工弹簧的弹性势能表达式为

式中：k_d1，k_d2，k_d3，k_d4分别为矩形平板四边法向位移弹簧的刚度；k_r1，k_r2，k_r3，k_r4分别为矩形平板四边法向转角弹簧的刚度。

1.2   多层板动力学理论建模

本节采用Layerwise理论对双层板（钢质平板+阻尼层）进行建模^[12]，各层之间采用独立的位移场描述，层间通过位移协调关系保证边界处位移及转角连续。

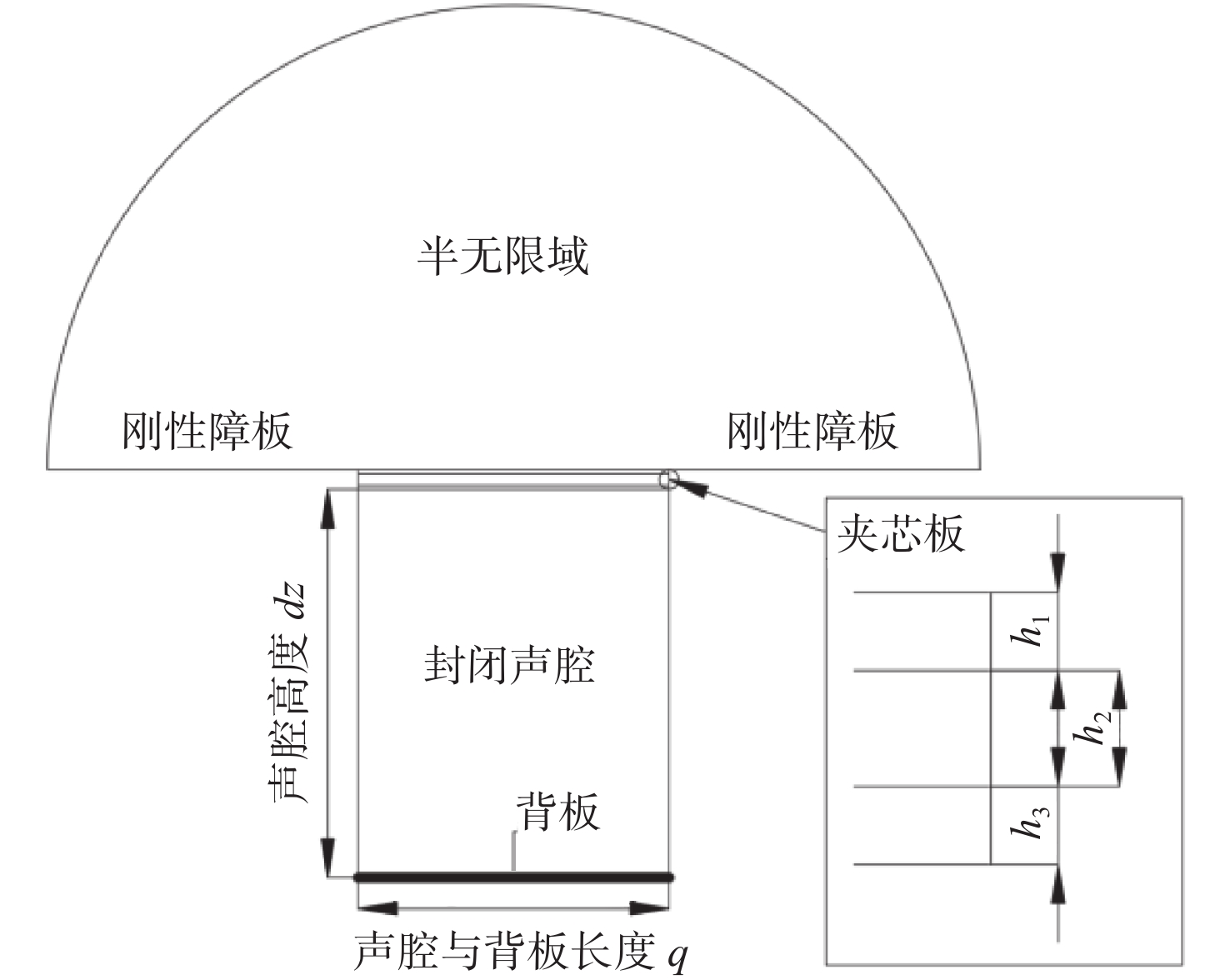
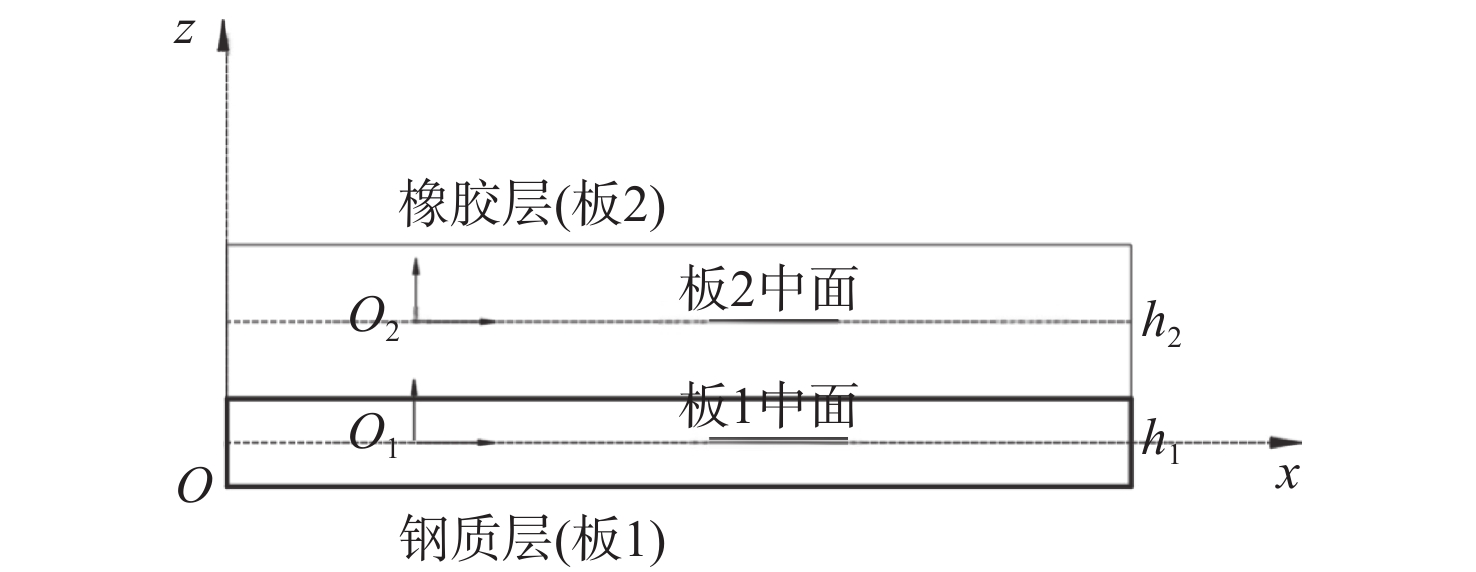
考虑到本节为钢质平板+阻尼层的双层板结构，而橡胶材料的刚度远小于钢板材料的刚度，因此将双层板结构的弯曲中面定为钢质平板的中面。令钢板为板1，其板厚为h₁，橡胶层为板2，其板厚为h₂；将双层板结构的参考坐标系原点定位于钢质平板中面处，其坐标系如图1所示图中，o₁和o₂分别表示板1、板2各自局部坐标系的原点。

图  1  双层板结构参考坐标系

Figure  1.  Reference coordinate system of double-layer plate structure

下载: 全尺寸图片 幻灯片

双层板结构中面（板1中面）处沿x，y，z方向的位移分别为u₀，v₀，w₀，板1的位移场可以写为

式中：θ_x1，θ_y1分别为板1变形后x，转y方向的转角；z₁为板1内部距其中面厚度方向的坐标。

同理，板2的位移场可以写为

式中：θ_x2，θ_y2为板2变形后x，y方向的转角；${{\textit{z}}_2}$为板2内部距其中面厚度方向的坐标。

分别采用改进的傅里叶级数作为u₀，v₀，w₀，θ_x1，θ_y1，θ_x2，θ_y2的试函数，其表达式为

式中：${M_j},{N_j}(j = 1,2,...,7)$，为u₀，v₀，w₀，θ_x1，θ_y1，θ_x2，θ_y2试函数的截断项数；A_mn，B_mn，C_mn，D_mn，E_mn，F_mn，G_mn为待定系数；A，B，C，D，E，F，G分别为由u₀，v₀，w₀，θ_x1，θ_y1，θ_x2，θ_y2试函数的未知系数组成的列向量；采用的改进型傅里叶级数f_m(x)，g_n(y)的具体表达式如式（1）所示。

双层板结构的应变能为各层应变能之和，即$U = {U_1} + {U_2}$，其中各层应变能的表达式如式（9）所示。

式中：下标i = 1，2，分别表示板1和板2的应变能；S为平板在xoy平面内的积分域；ε_xi，ε_yi，γ_xyi，γ_yzi，γ_zxi分别为第i层沿x，y，z方向的正应变和切应变；σ_xi，σ_yi，τ_xyi，τ_yzi，τ_zxi分别为第i层内部沿各方向的正应力及切应力。

同理，双层板的动能$T = {T_1} + {T_2}$，各层的动能如式（10）所示。

三层夹芯板与双层板采用的理论假设一致，只不过结构变为钢质平板（板1）+橡胶夹芯（板2）+钢质平板（板3），各层之间满足位移及转角连续条件。

采用改进的傅里叶级数作为u₀，v₀，w₀，θ_x1，θ_y1，θ_x2，θ_y2，θ_x3，θ_y3的试函数，其表达式为

在此基础上，便可分别计算三层夹芯板的各层应变能之和，即$U = {U_1} + {U_2} + {U_3}$，其中各层应变能的计算方式与式（9）一致，同样，也可分别计算三层夹芯板的动能T及边界弹簧的弹性势能${U_{\text{s}}}$ 。

1.3   结构−声场耦合处理

本文的研究对象为嵌在无限大刚性障板上的夹芯平板，夹芯平板的一侧为半无限域声场，另一侧为以夹芯平板作为端面的封闭声腔，该声腔的另一侧与背板耦合，如图3所示。

图  2  双面板−声腔耦合模型示意图

Figure  2.  Schematic diagram of coupled model of double panel and acoustic cavity

下载: 全尺寸图片 幻灯片

图  3  有限元模型示意图

Figure  3.  Schematic diagram of finite element model

下载: 全尺寸图片 幻灯片

其中，半无限域声场在平板表面任意一点$\left( {x,y} \right)$处的声压可由Rayleigh积分得到：

式中：${\rho _f}$为半无限域声场介质密度；${k_\omega } = {\omega \mathord{\left/ {\vphantom {\omega {{c_f}}}} \right. } {{c_f}}}$，为辐射声场的波数，其中${c_f}$为半无限域声场介质声速；$R = \sqrt {{{\left( {{x_1}-x} \right)}^2} + {{\left( {{y_1}-y} \right)}^2}}$。

声场与结构振动之间的耦合效应以声压做功的形式给出，声场在结构表面的声压对平板所做的功为

式中：S为平板在xoy平面内的积分域；p_c为声压试函数。

对于封闭的声腔，声腔内稳态声压的表达式可由展开级数表达；与弹性边界下平板振动位移试函数的选取类似，有限声腔内声压的试函数可以采用三维改进的傅里叶级数，用以满足声腔不同阻抗边界处的空间导数连续问题。

文献[16]分析了不同阻抗边界下声腔与薄板的耦合振动差异，而本文研究的六面体柱形声腔在其上端面与夹芯平板耦合，在其下端面与背板耦合，用于模拟声呐腔一边与导流罩耦合，一边与背板的耦合，在其余方向假设没有能量传递。将声腔其余的4个侧面设为刚性边界，因此声压试函数p_c可以写为

式中：M_x，M_y，M_z分别为声压试函数关于x，y，z展开级数的截断项数； ${J_{{m_x}{m_y}{m_{\textit{z}}}}},{a_{{m_x}{m_y}}},{b_{{m_x}{m_y}}}$为待定系数；J为由各项待定系数组成的列向量；$\varsigma$为由试函数展开项与补充项组成的列向量；${\lambda _{{m_x}}} = {{{m_x}{\text{π}} } / {{a_x}}}$，${\lambda _{{m_y}}} = {{{m_y}{\text{π}} } / {{b_y}}}$，${\lambda _{{m_{\text{{\textit{z}}}}}}} = {{{m_{\textit{z}}}{\text{π}} }/{{d_{\textit{z}}}}}$，其中${a_x},{b_y},{d_{\textit{z}}}$分别为柱形声腔的长、宽、高；${\chi _{1{\textit{z}}}}({\textit{z}}) = {\textit{z}}{({{\textit{z}} /{{d_{\textit{z}}}-1}})^2}$，${\chi _{2{\textit{z}}}}({\textit{z}}) = {{\textit{z}}^2}({{\textit{z}} / {{d_{\textit{z}}}-1}})$为z方向上的补充项，用以保证声压在声腔上、下端面导数连续。

封闭声腔的势能U_c和动能T_c分别为

式中：${\rho _{\text{c}}}$和${c_{\text{c}}}$分别为封闭声腔内介质的密度和声速；${V_{\text{c}}}$为封闭声腔内的声场域；${\varsigma _x},{\varsigma _y},{\varsigma _{\textit{z}}}$分别为由试函数展开项与补充项组成的列向量对x，y，z的一阶导数。

1.4   双面板和声腔耦合系统响应

根据Hamilton原理，夹芯板、背板和柱形声腔各自的能量泛函应满足对各自试函数的待定系数取极值，即

式中：L_p-s为夹芯板能量泛函；L_c为声腔能量泛函；L_p-b为平板能量泛函；${U_{{\text{p-s}}}}$为夹芯板的应变能；${U_{{\text{s-s}}}}$为夹芯板边界弹簧的弹性势能；${T_{{\text{p-s}}}}$为夹芯板的动能；${T_{{\text{p-b}}}}$为夹芯板的动能；${W_{\text{r}}}$为半无限域辐射声场的做功；${W_{{\text{c-s}}}}$为封闭声腔内声压对夹芯板的做功；${W_{{\text{c-b}}}}$为封闭声腔内声压对夹芯板的做功；O为夹芯板位移函数的待定系数列向量；${U_c}$为封闭声腔势能，${T_c}$为封闭声腔；J为声腔内声压函数待定系数的列向量；${U_{{\text{p-b}}}}$为平板的应变能；${U_{{\text{s-b}}}}$为平板边界弹簧的弹性势能；${W_{\text{F}}}$为点激励做功；${A_{\rm{P}}}$为平板位移函数的待定系数列向量。

将式（1）～式（17）代入式（18），可以得到夹芯板−声腔−背板耦合系统的动力学方程为

式中：${{\boldsymbol{K}}_{{\text{p-s}}}}$为夹芯平板刚度矩阵；${{\boldsymbol{K}}_{{\text{s-s}}}}$为夹芯平板的边界弹簧刚度矩阵；${{\boldsymbol{M}}_{{\text{p-s}}}}$为夹芯平板的质量矩阵；${M_{\text{r}}}$为半无限声场与夹芯板的耦合矩阵；${\rho _{\text{c}}}c_{\text{c}}^2{\boldsymbol{R}}_{{\text{c-s}}}^{\text{T}}$为声腔与夹芯板之间的耦合矩阵；${{\boldsymbol{R}}_{{\text{c-s}}}}$为夹芯板与声腔之间的耦合矩阵；${{\boldsymbol{K}}_{\text{c}}}$为柱形声腔的刚度矩阵；${{\boldsymbol{M}}_{\text{c}}}$为柱形声腔的质量矩阵；${\rho _{\text{c}}}c_{\text{c}}^2{\boldsymbol{R}}_{{\text{c-b}}}^{\text{T}}$为声腔与背板之间的耦合矩阵；${{\boldsymbol{K}}_{{\text{p-b}}}}$为背板刚度矩阵；${{\boldsymbol{K}}_{{\text{s-b}}}}$为背板的边界弹簧刚度矩阵；${{\boldsymbol{R}}_{{\text{c-b}}}}$为背板与声腔之间的耦合矩阵；${{\boldsymbol{M}}_{{\text{p-b}}}}$为背板的质量矩阵；F为简谐点激励力矩阵。

求解方程（18），可得出夹芯板位移函数待定系数的列向量O、声腔内声压函数待定系数的列向量J和背板位移函数的待定系数${{\boldsymbol{A}}_{\rm{P}}}$，分别代入式（2），式（8），式（11）和式（14），即可得出点激励作用下的背板位移、夹芯板位移和封闭声腔内任意点处的声压。

2.   算法验证

分别采用本文方法和有限元仿真软件Comsol计算水下夹芯板−声腔−平板在简支边界约束下的振动响应。其中，夹芯板第1层和第3层面板的材质为钢，第2层芯层的材质为橡胶，其尺寸以及材料参数如表1所示；夹芯板两侧分别与半无限声场以及封闭声腔耦合，封闭声腔和半无限声场介质均为水，其参数和封闭声腔尺寸如表2所示；封闭声腔另一面与平板耦合，平板尺寸与夹芯板相同，材料为钢，厚度为2 mm。

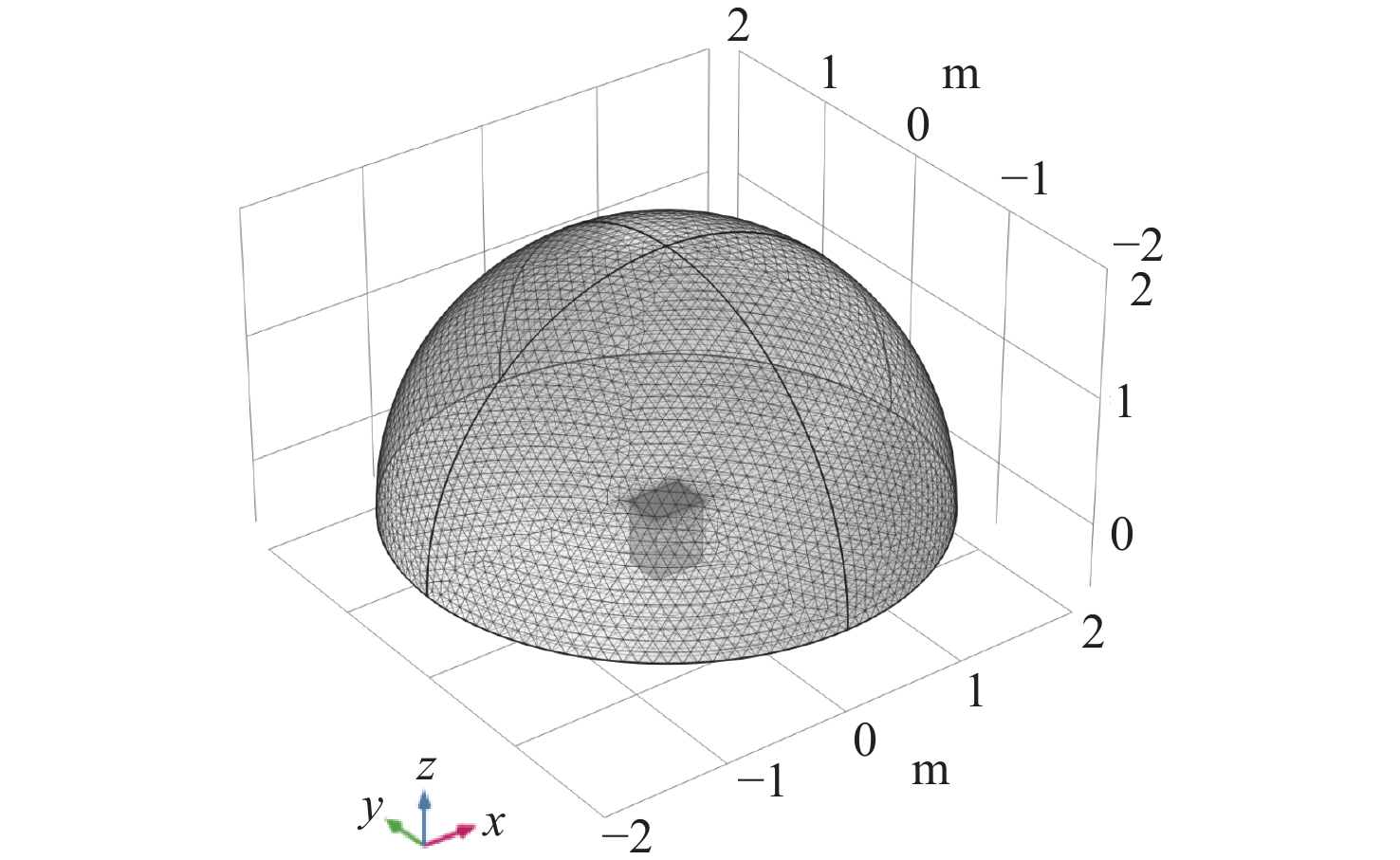
表  1  夹芯板尺寸以及各层材料参数

Table  1.  Sandwich panel size and material parameters of each layer

参数		数值
夹芯板长度a/m		0.4
夹芯板宽度b/m		0.3
第1层平板厚度h1/m		0.001
第2层平板厚度h2/m		0.003
第3层平板厚度h3/m		0.001
钢	弹性模量E1/Pa	$2.06 \times {10^{11}}$
	泊松比μ1	0.3
	密度ρ1/(kg∙m−3)	7 850
	结构损耗因子η	0.01
橡胶	弹性模量E2/P	$7.84 \times {10^6}$
	泊松比μ2	0.47
	密度ρ2/(kg∙m−3)	2 000
	结构损耗因子η	0.1

下载: 导出CSV 

| 显示表格

表  2  封闭声腔尺寸以及声介质材料参数

Table  2.  Size of enclosed acoustic cavity and parameters of acoustic dielectric material

参数	数值
声腔长度ax/m	0.4
声腔宽度by/m	0.3
声腔高度dz/m	0.5
声介质密度ρca/(kg∙m−3)	1 000
声介质声速cca/(kg∙m−3)	1 500

下载: 导出CSV 

| 显示表格

有限元模型如图3所示。在有限元软件Comsol中建立半球与长方体的联合模型，长方体长0.4 m，宽0.3 m，高0.5 m，半球半径为2 m。将长方体与半球耦合的上表面设置为夹芯板，另一侧下表面均设置为平板。长方体其余四面均设置为硬声学边界。将半球中曲面设置为完美匹配层，平面设置为硬声学边界。半球与长方体内部材料均设置为水，分别模拟半无限域与封闭腔。

以夹芯板的中心点为坐标原点建立三维直角坐标系，x轴平行于夹芯板长0.4 m的边，z轴正向指向背板。在背板（0.1 m，0.05 m，0.5 m）处施加单位力激励。在背板上取点A（0.05 m，0.1 m，0.5 m）和点B（0.15 m，−0.05 m，0.5 m)，在声腔中取点C（0.05 m，0.1 m，0.25 m）和点D（0.15 m，−0.05 m，0.25 m），分别计算其振动响应。

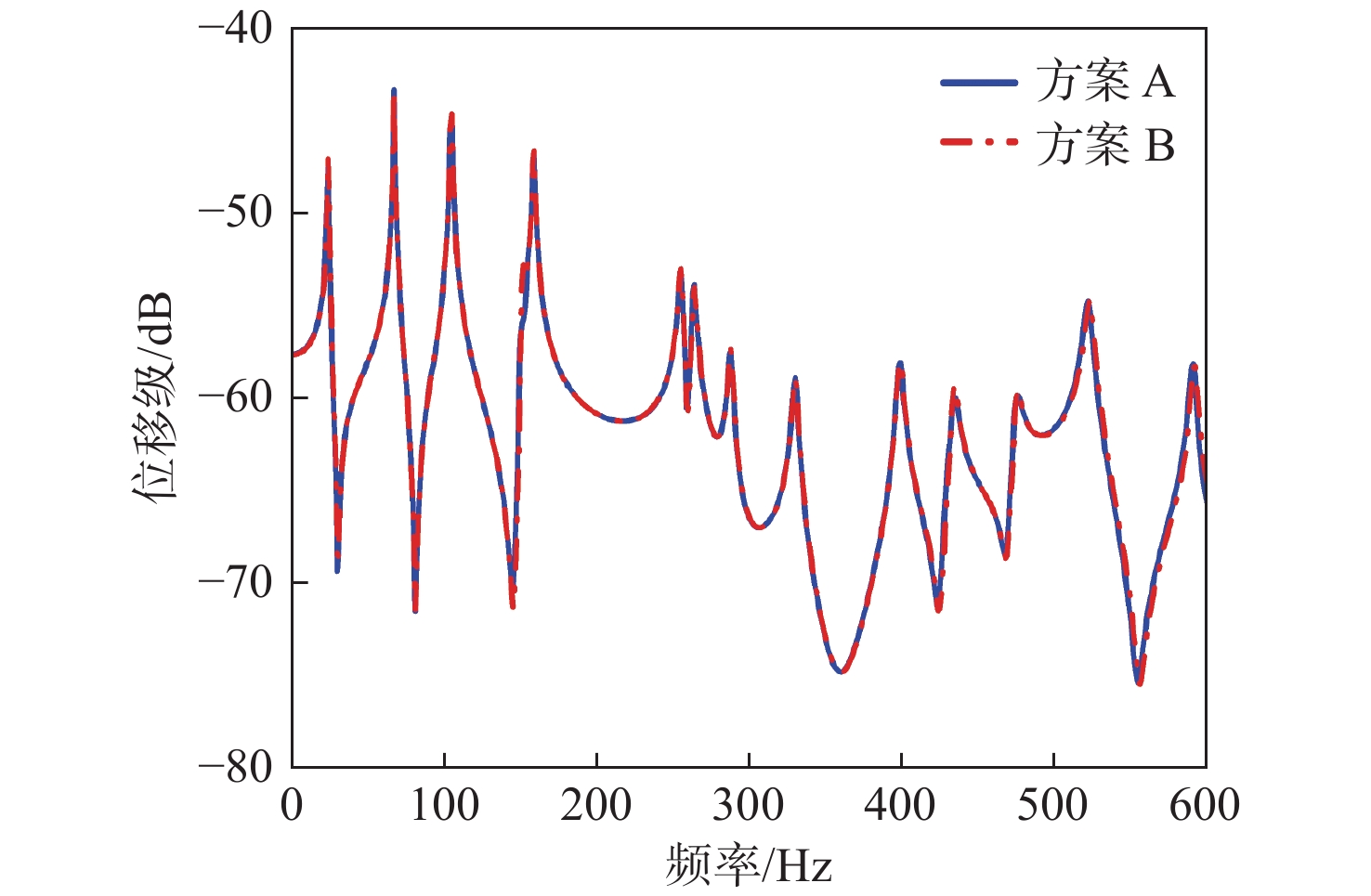
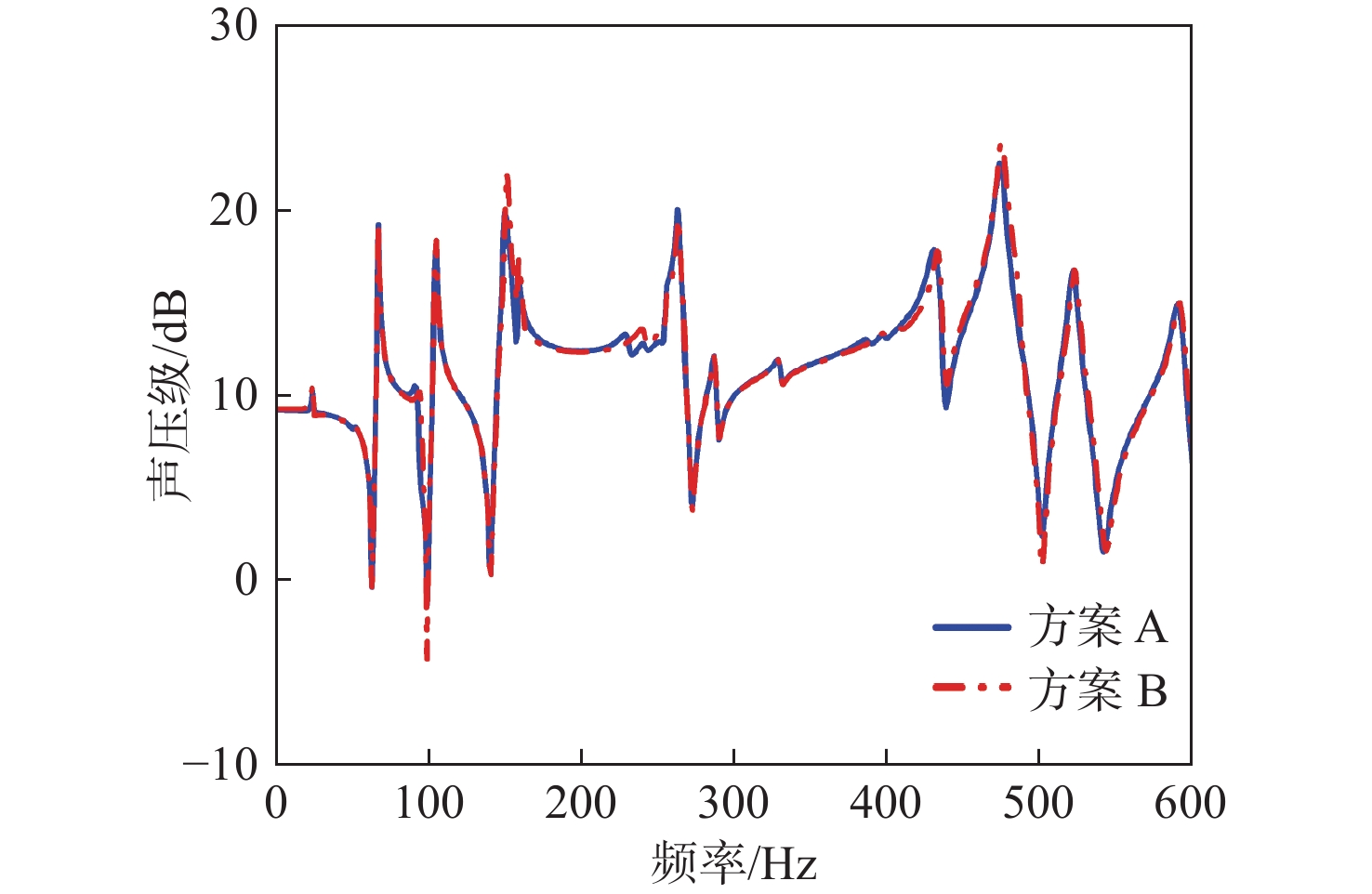
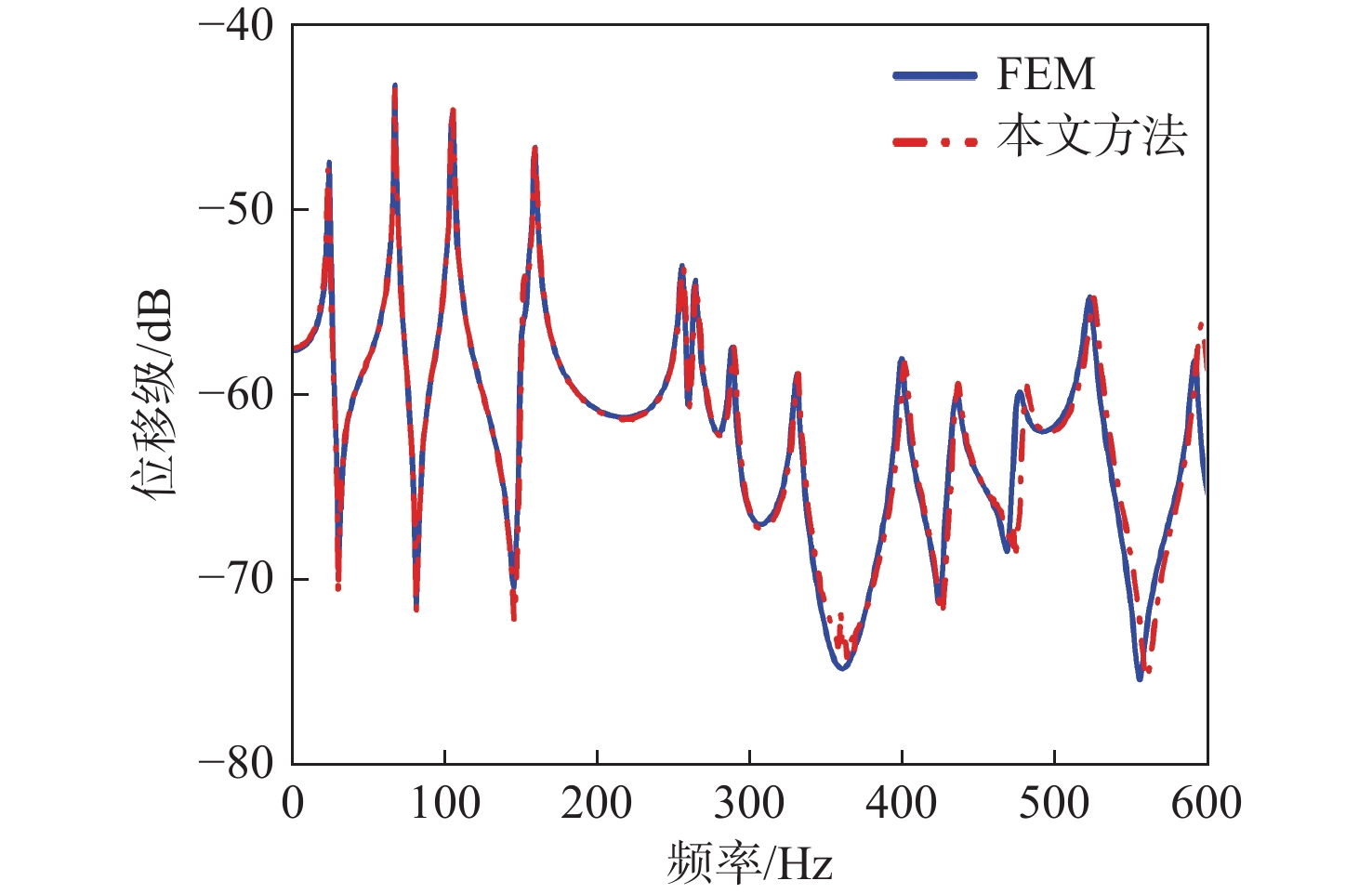
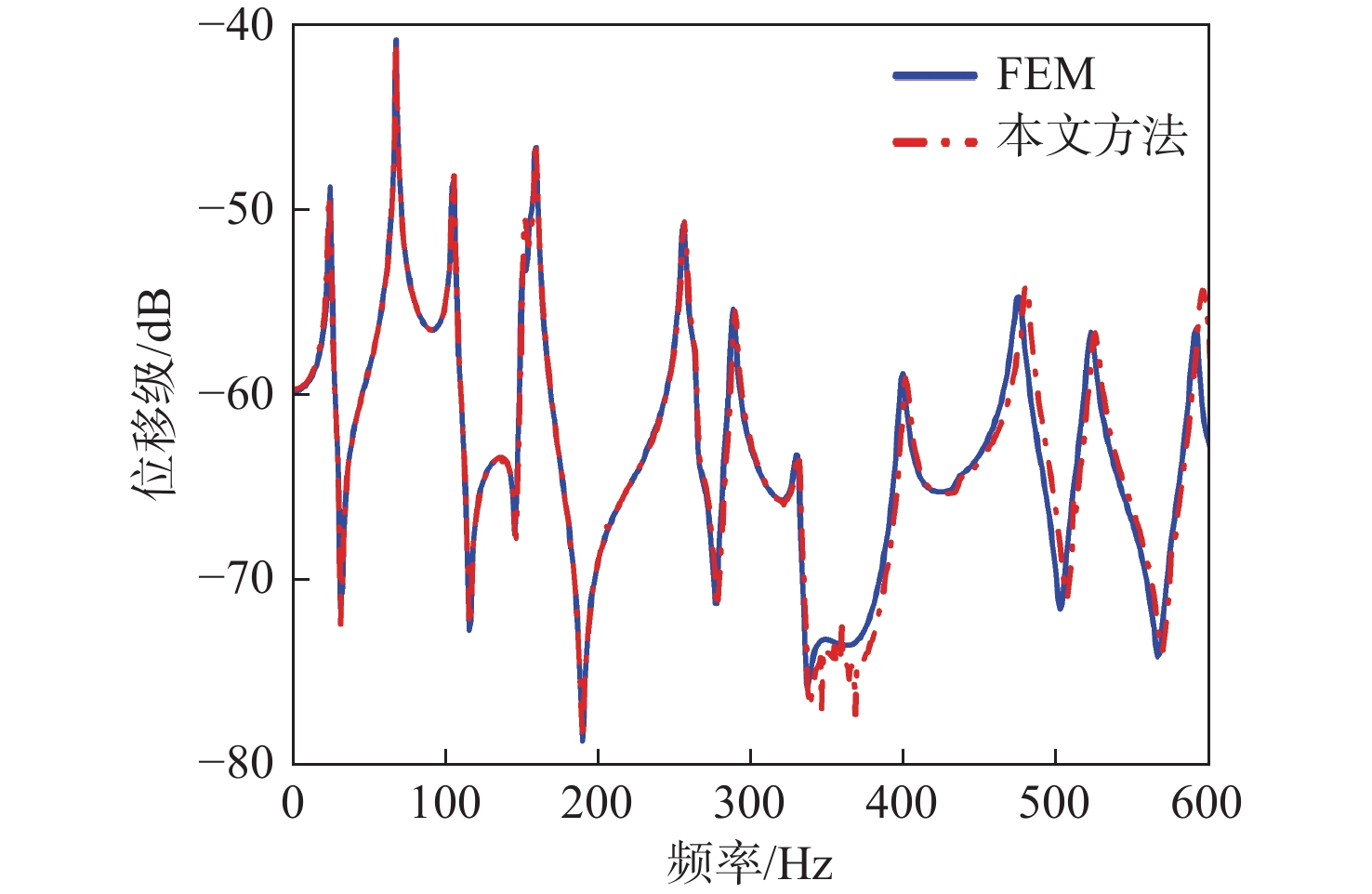
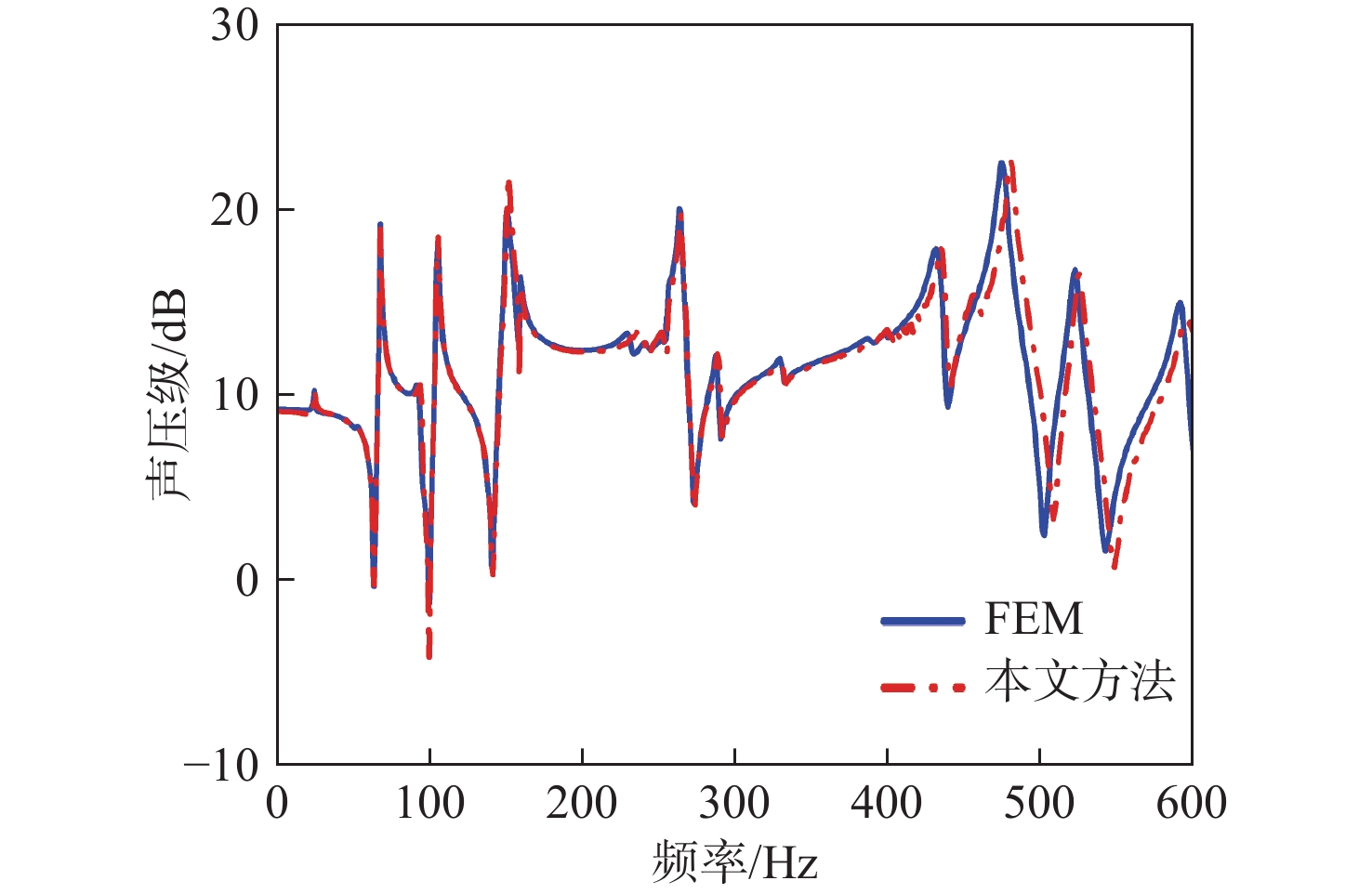
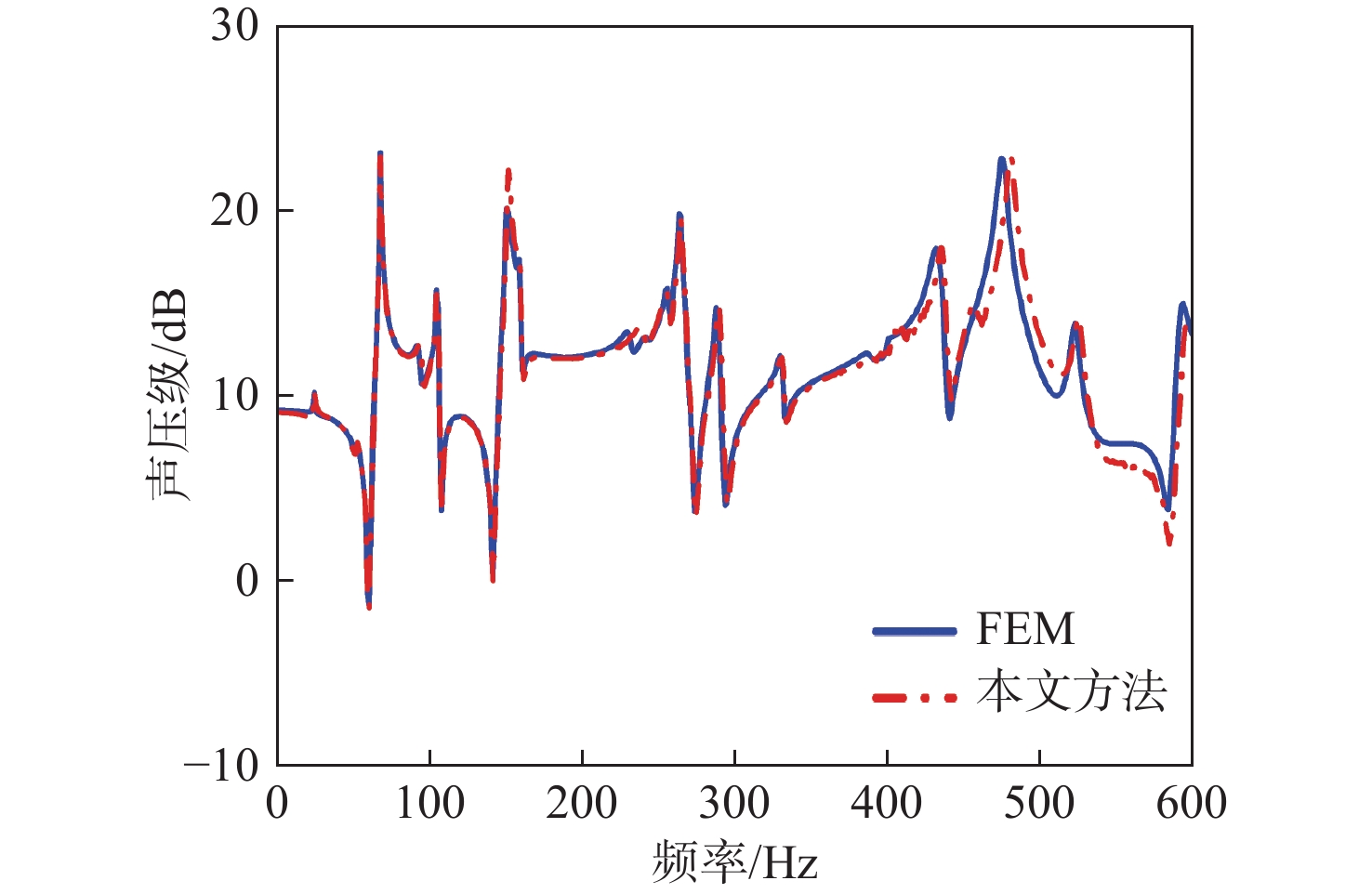
采用有限元软件Comsol在不同网格大小下计算振动响应，进行收敛性分析，其中方案A中壳结构单元尺寸为0.025 m×0.025 m，封闭声腔中单元尺寸为0.025 m×0.025 m×0.1 m，半无限域取边长为0.2 m的四面体网格。方案B中壳结构单元尺寸为0.01 m×0.01 m，封闭声腔中单元尺寸为0.01 m×0.01 m×0.05 m，半无限域取边长为0.1 m的四面体网格。计算结果如图4和图5所示。位移级计算公式为20 lg(w)，其中w为响应提取点位移大小。声压级计算公式为$20{\log _{10}}(P)$,其中P为响应提取点声压大小。

图  4  A点位移级

Figure  4.  A-point displacement level

下载: 全尺寸图片 幻灯片

图  5  C点声压级

Figure  5.  C-point sound pressure level

下载: 全尺寸图片 幻灯片

由图4和图5可知，方案B满足计算精度。

由图6～图9可知，采用本文方法计算得到的背板A点和B点的位移频响曲线，以及声腔内部C点和D点的声压频响曲线与有限元结果吻合良好，验证了本文对于水下耦合模型动力学建模方法的正确性。

图  6  A点位移级

Figure  6.  A-point displacement level

下载: 全尺寸图片 幻灯片

图  7  B点位移级

Figure  7.  B-point displacement level

下载: 全尺寸图片 幻灯片

图  8  C点声压级

Figure  8.  C-point sound pressure level

下载: 全尺寸图片 幻灯片

图  9  D点声压级

Figure  9.  D-point sound pressure level

下载: 全尺寸图片 幻灯片

3.   耦合系统振动特性分析

3.1   背板为平板和阻尼板的响应对比

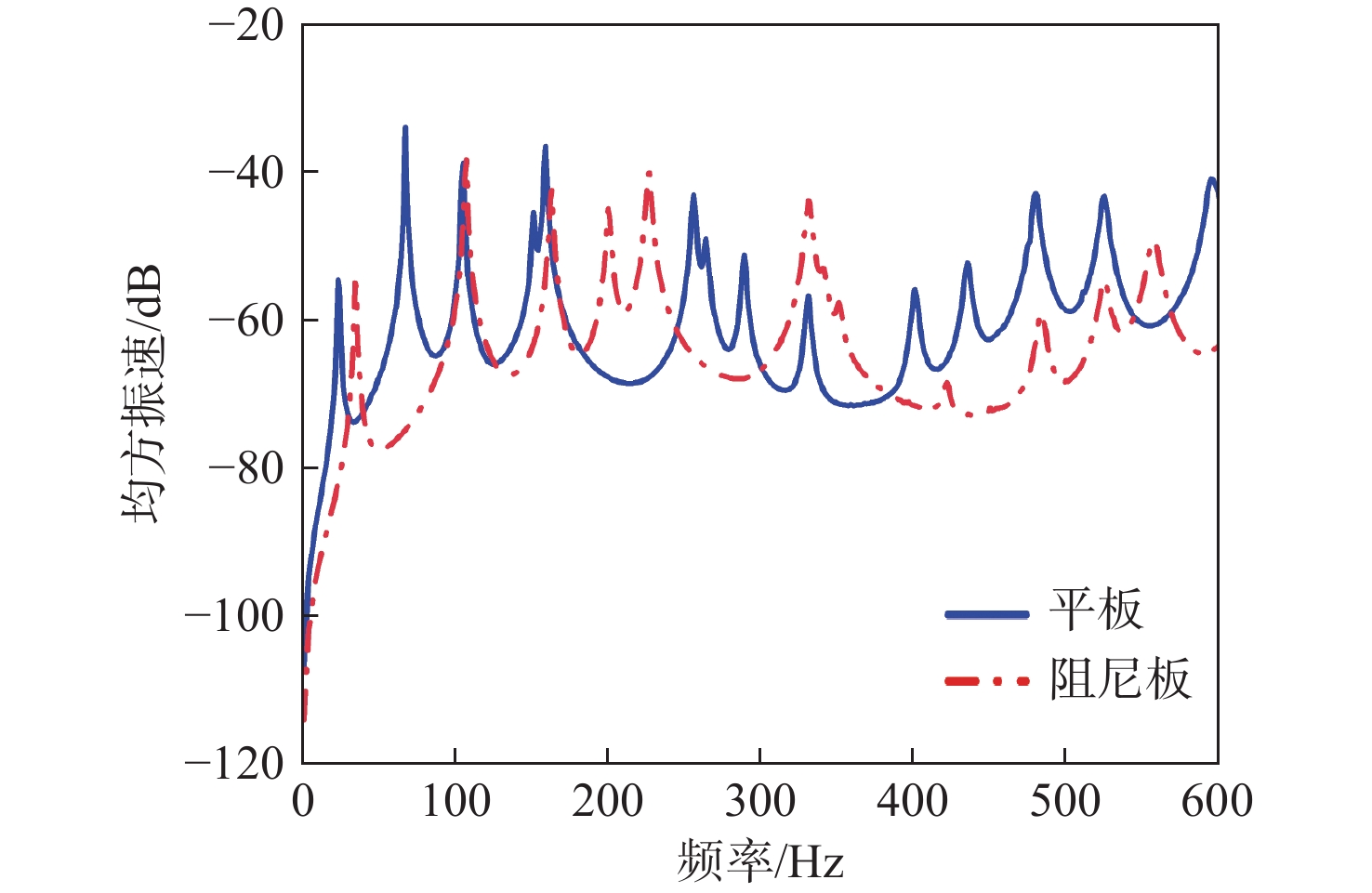
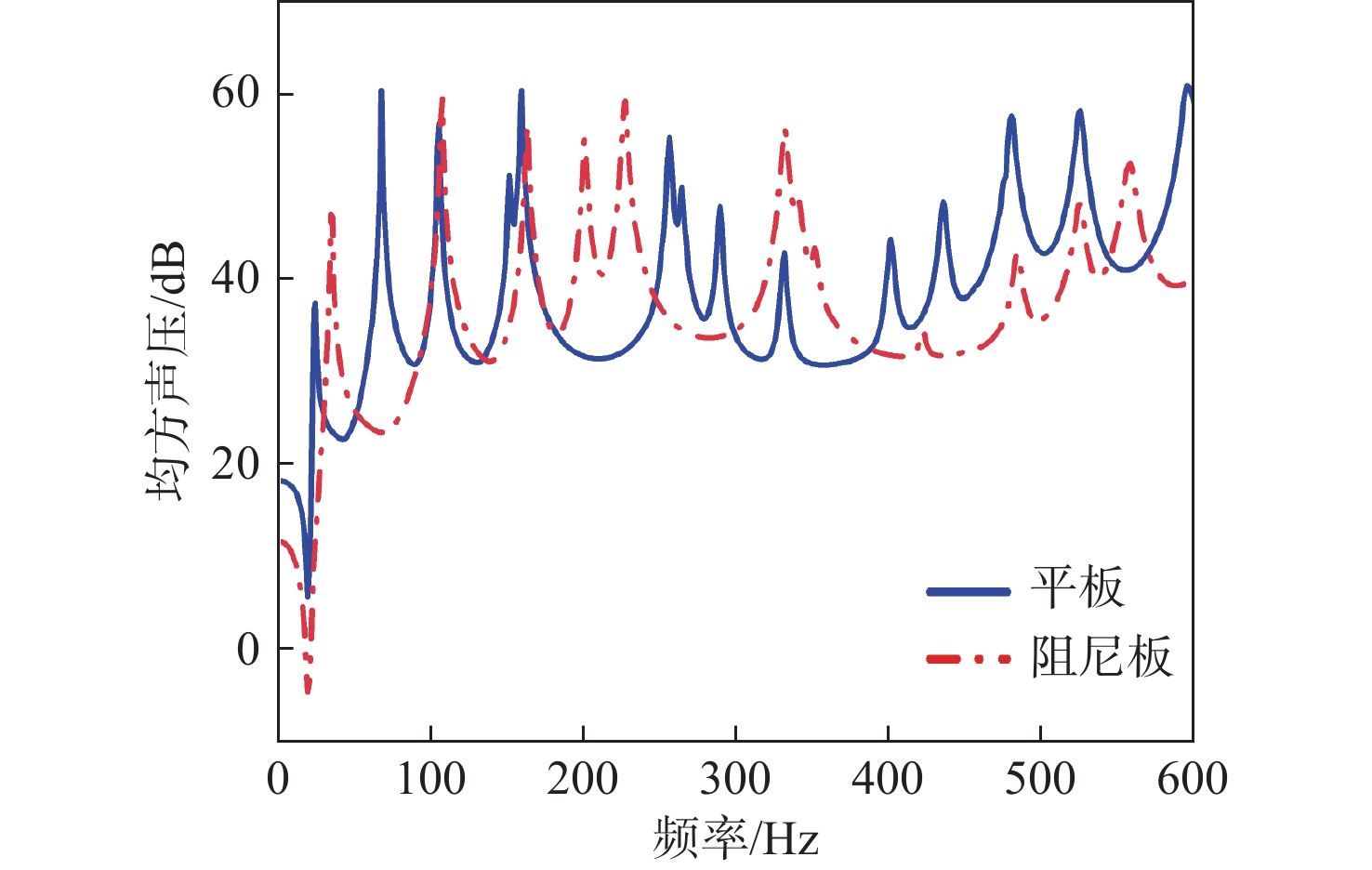
本节计算模型与第2节一致。为研究背板的阻尼层对耦合系统响应的影响，分别计算单点激励下有/无背板阻尼的系统振动响应，得到不同方案下背板在1～600 Hz时的板面均方振速曲线如图10所示，不同方案下声腔中面的均方声压曲线如图11所示。背板阻尼为厚0.005 m的橡胶层，橡胶层结构损耗因子取0.5，密度为1 100 kg/m³，泊松比为0.49，弹性模量为7.84×10⁶ Pa。声腔高度为0.5 m，声腔中面为纵坐标z = 0.25 m的封闭声腔中平面。均方振速级计算式为$20{\log _{10}}(V)$，其中V为背板振速均方根值；均方声压级计算式为20 lg(P_RMS)，其中P_RMS为声腔中面声压均方根值。

图  10  平板与阻尼板背板均方振速对比

Figure  10.  Comparison of mean square vibration velocity between plate and damped plate backplane

下载: 全尺寸图片 幻灯片

图  11  平板与阻尼板声腔中面均方声压对比

Figure  11.  Comparison of mean square sound pressure in plate and damped plate cavity

下载: 全尺寸图片 幻灯片

由图10可知，阻尼板的均方振速整体略低于平板，总级降低了3.31 dB，表明板由于贴附橡胶层，增强了系统的耗散，故而降低了振动响应。由图11可知，当背板为阻尼板时，声腔中面均方声压在大部分频段内略低于平板，总级降低了2.92 dB。

3.2   背板厚度影响分析

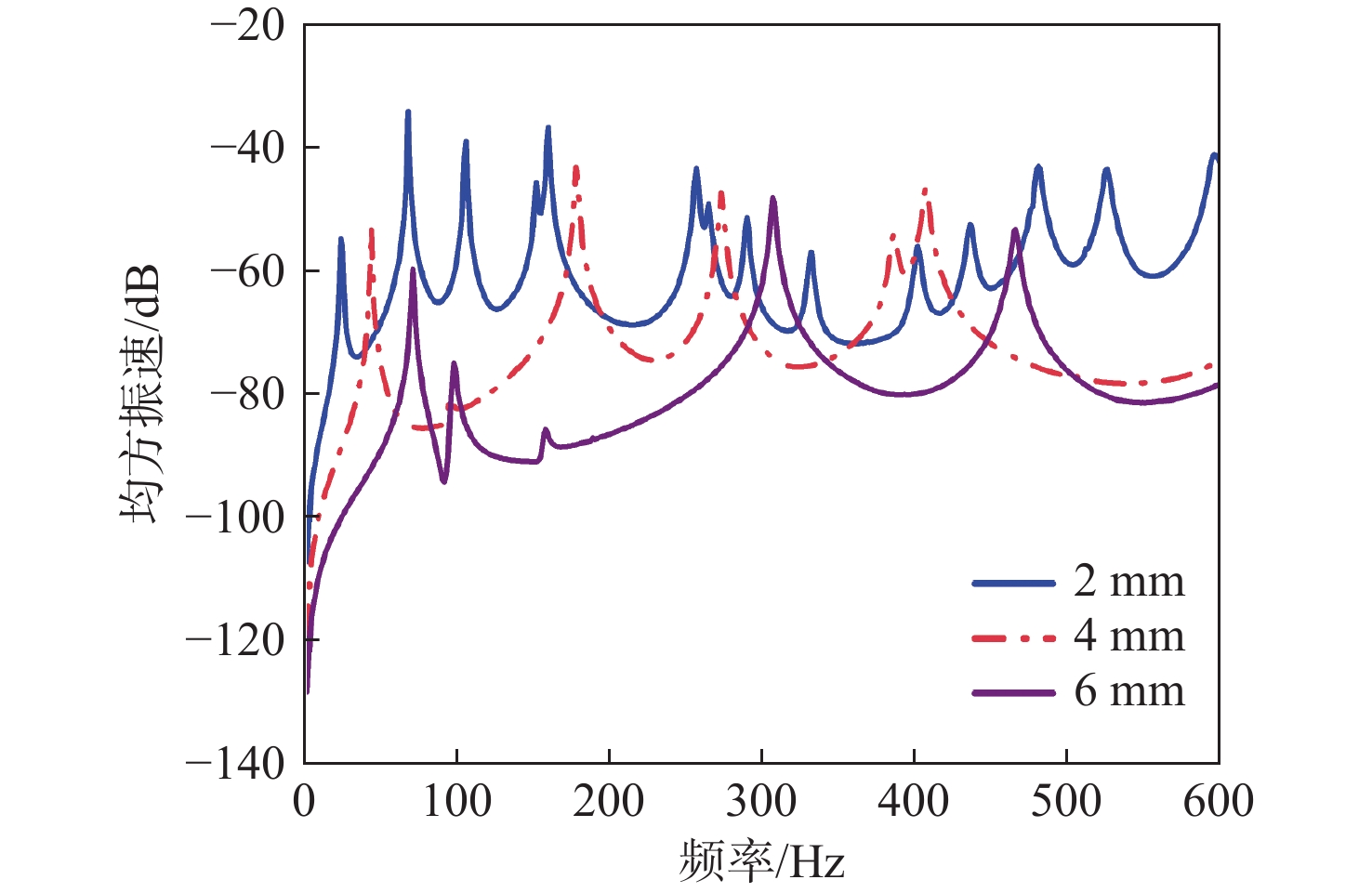
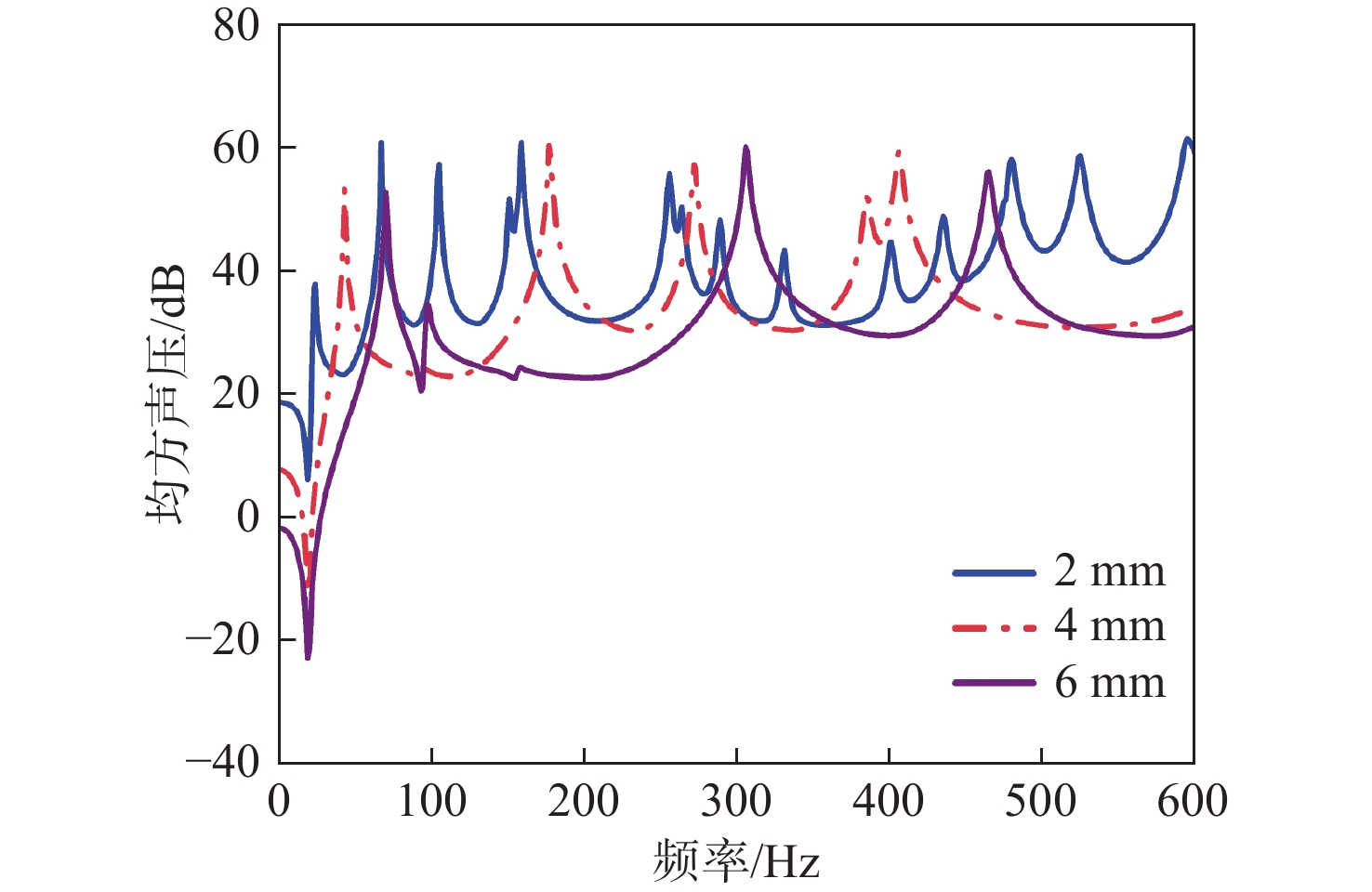
为研究耦合系统中背板厚度对耦合系统响应的影响，设置背板厚度为2，4，6 mm，分别计算3种方案下的机械激励振动响应，得到不同厚度下单层板1～600 Hz时的板面均方振速曲线如图12所示，不同方案下声腔中面的均方声压曲线如图13所示。

图  12  不同背板厚度背板均方振速对比

Figure  12.  Comparison of mean square vibration velocity of backplane with different backplane thickness

下载: 全尺寸图片 幻灯片

图  13  不同背板厚度声腔中面均方声压对比

Figure  13.  Comparison of mean square sound pressure in acoustic cavity with different backplane thickness

下载: 全尺寸图片 幻灯片

由图12可知，随着背板厚度的增加，背板的均方振速整体减小，6 mm厚背板的均方振速明显低于2 mm厚的背板，表明增加背板厚度能够有效抑制振动。由图13可知，6 mm厚背板的声腔中面均方声压基本低于2 mm厚背板的声腔中面均方声压，这是因为在低频段内增加背板厚度可提高刚度，抑制振动幅度，并减少共振现象。

3.3   声腔高度影响分析

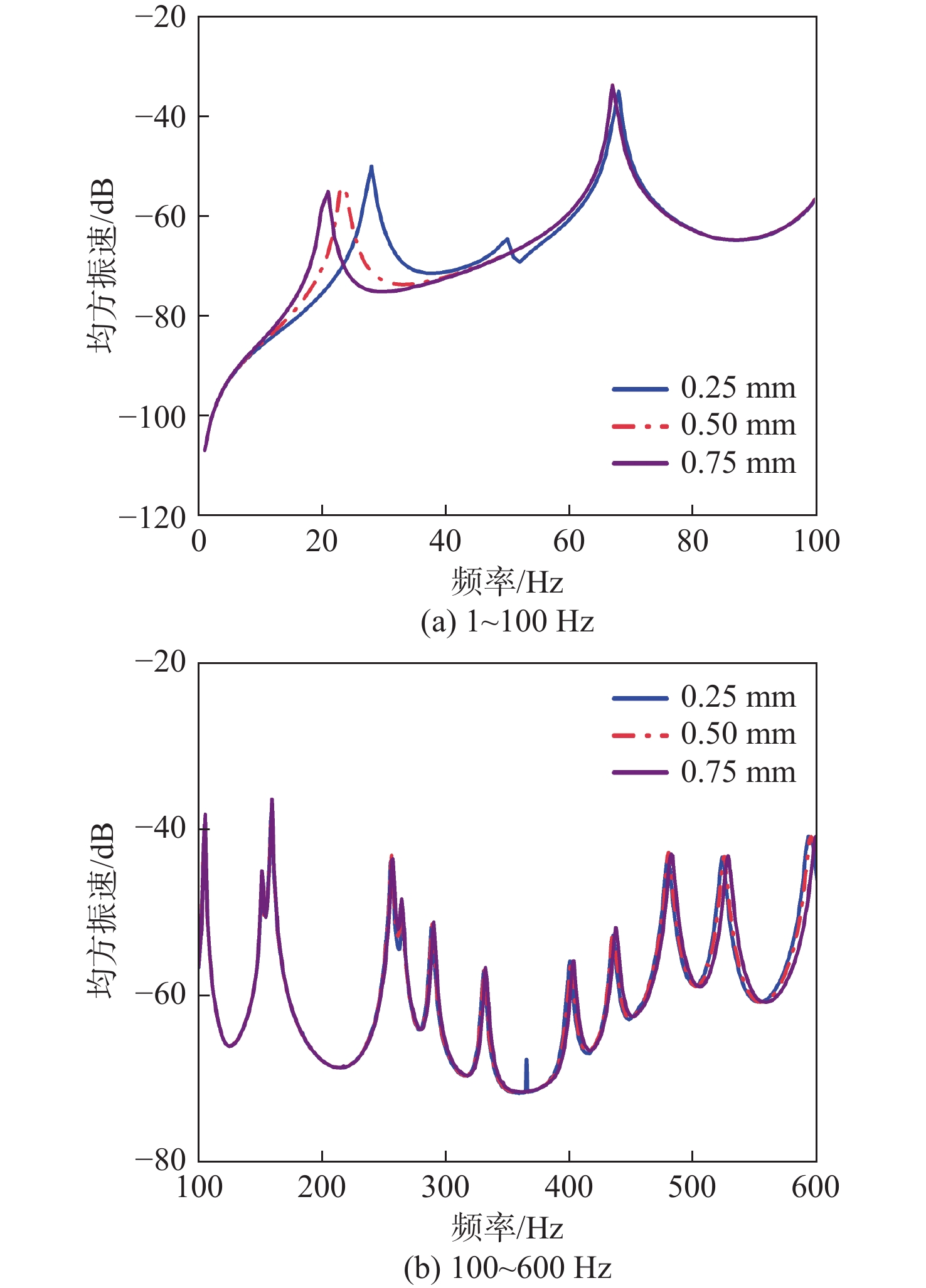
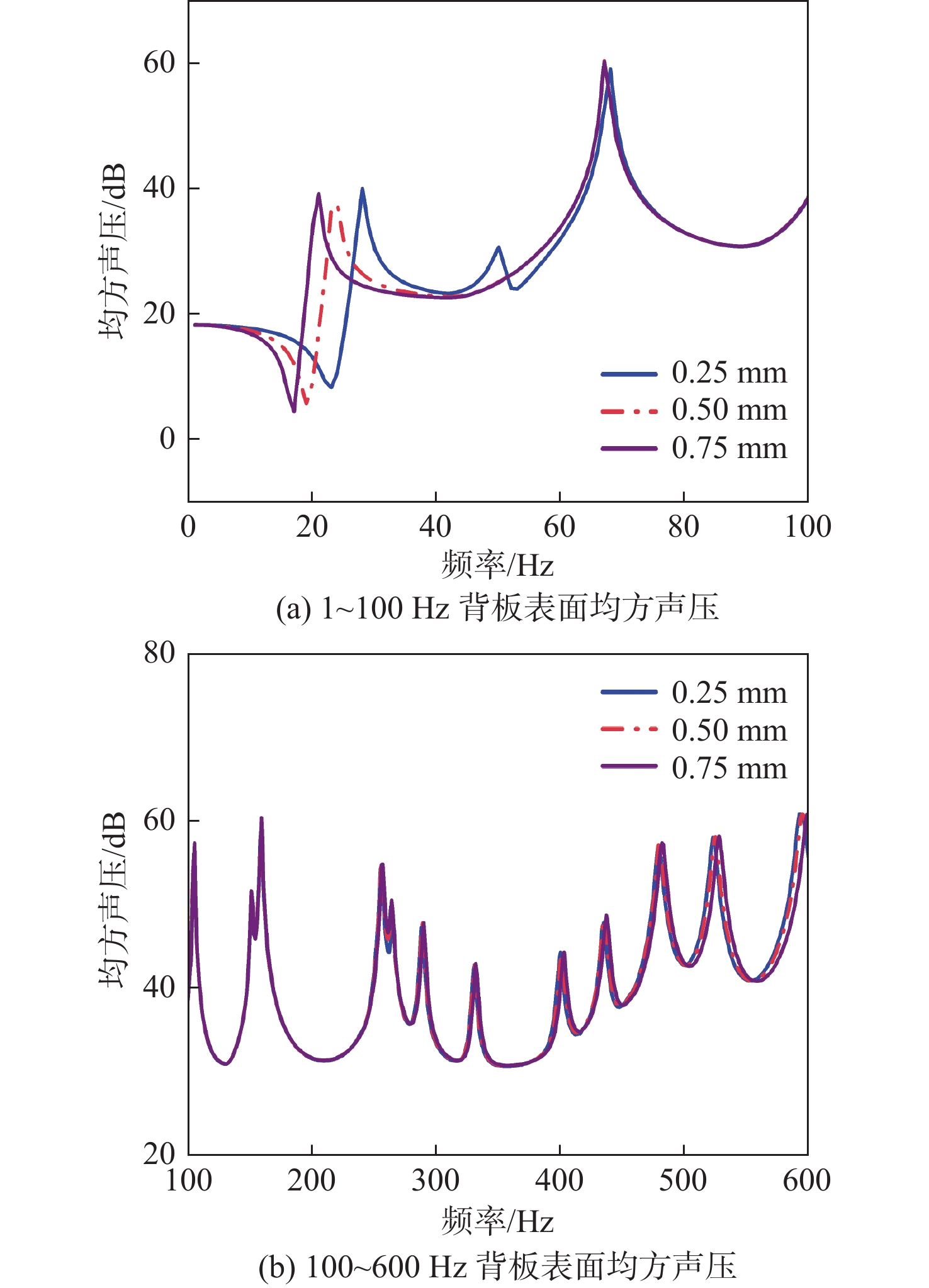
为研究耦合系统中声腔高度对耦合系统响应的影响，设置声腔高度分别为0.25，0.5和0.75 m。分别计算不同方案下背板在1～600 Hz时的板面均方振速曲线如图14所示，不同方案下背板表面的均方声压曲线如图15所示。由于声腔高度对于系统响应的影响主要体现在第1阶峰值之前，故将频率范围为1～600 Hz的频响曲线图分为1～100 Hz和100～600 Hz两张图。

图  14  不同声腔高度背板表面均方振速对比

Figure  14.  Comparison of mean square velocity of backplane surface at different cavity heights

下载: 全尺寸图片 幻灯片

图  15  不同声腔高度背板表面均方声压对比

Figure  15.  Comparison of mean square sound pressure on backplane surface with different cavity heights

下载: 全尺寸图片 幻灯片

由图14可知，3种声腔高度下的夹芯板板面均方振速大小量级接近，声腔高度对夹芯板板面均方振速的影响主要体现在第1阶响应峰值对应的频率，声腔高度越大，第1阶响应峰值对应的频率越低，且振速更大。这是因为声腔高度越大，结构振动与声腔辐射之间在低频的耦合效应越强。由图15可知，声腔高度对背板表面均方声压的影响与背板振速类似。

4.   结　论

本文基于薄板理论建立了平板的动力学模型，基于Layerwise理论建立了阻尼板和夹芯板结构的动力学模型，通过将结构振动与有限封闭声腔以及半无限声场耦合，运用能量泛函推导出水下夹芯板−腔−平板（阻尼板）耦合模型的响应函数。由于本文采用的声压试函数和夹芯板位移试函数均为改进型展开级数，使得本文模型适用于不同结构边界条件。通过与有限元方法结果进行对比，验证了本文耦合模型动力学建模方法的正确性。通过参数分析，主要得到以下结论：

1）阻尼板的均方振速整体低于平板，总级降低了3.31 dB。当背板为阻尼板时，声腔中面均方声压在大部分频段内略低于平板，总级降低了2.92 dB。

2）随着背板厚度的增加，背板的均方振速整体减小，6 mm厚背板的均方振速明显低于2 mm厚的背板。6 mm厚背板的声腔中面均方声压基本低于2 mm厚背板的声腔中面均方声压。

3）声腔高度对于结构−声腔耦合系统的影响主要集中在系统的首阶响应峰值之前，声腔高度越大，第1阶响应峰值对应的频率越低，且振速更大。