Local perception-based path planning for unmanned surface vehicles using deep reinforcement learning
-
摘要:目的
针对海上搜救任务中无人艇感知范围有限导致的路径规划效率低、鲁棒性差的问题,提出一种基于局部状态感知的无人艇路径规划方法。
方法首先,采用Soft Actor-Critic算法,设计基于局部感知的奖励函数,并结合特征增强训练方法,通过提取环境关键特征并在随机特征环境中训练,提升有限感知条件下的路径规划采样效率和鲁棒性。然后,提出一种基于局部感知域的迭代航路点规划方法,有效协调局部与全局目标,最终实现在海上搜救任务中的高效路径规划。
结果仿真结果显示,所提出的方法在特征环境中路径规划成功率达到98%以上,且在海上搜救任务中完成率超过93%,对不确定环境表现出了较好的鲁棒性和适应性。
结论所提出的基于局部状态感知的无人艇路径规划方法解决了深度强化学习在海上搜救任务中应用问题,可为强化学习算法在实际工程中的应用提供技术支持。
Abstract:ObjectiveMaritime rescue missions require efficient and reliable path planning for unmanned surface vehicles (USVs). However, these missions are challenged by the limited sensing capabilities of USVs operating in vast and uncertain environments with randomly distributed obstacles. This study addresses the issues of low path planning efficiency and poor robustness resulting from restricted perception range. To tackle these challenges, a novel local observation-based path planning approach is proposed for USVs in maritime rescue missions.
MethodThe proposed approach integrates three key methodological innovations. First, the soft actor-critic (SAC) algorithm is employed with a reward function tailored to local observation, which rewards efficient goal-reaching and penalizes obstacle collisions. This design helps balance exploration and exploitation in uncertain environments. Second, a feature-enhanced soft actor-critic (FESAC) algorithm is introduced to improve training efficiency and model robustness. It extracts key environmental features and employs a randomized training environment with strategically placed obstacles to enhance sampling efficiency. During training, obstacle positions, USV starting points, and goals are randomly reset across episodes, encouraging the model to learn generalizable navigation strategies instead of memorizing specific scenarios. Third, an adaptive waypoint planning algorithm is developed based on local perception domains to effectively coordinate local obstacle avoidance with global goal-reaching behavior. Waypoints are dynamically selected within the USV's perception radius using a weighted objective function that balances proximity to the goal and distance from obstacles. This decomposes the complex global path planning task into a series of manageable local planning problems.
ResultsComprehensive simulation experiments validate the effectiveness of the proposed approach. In feature-rich environments with randomly distributed obstacles, the method achieves a success rate exceeding 98%, significantly outperforming traditional methods. In simulated maritime rescue missions over 1,000 m×1,000 m areas with 20-50 randomly placed obstacles, the method maintains a task completion rate exceeding 93% under appropriate parameter configurations. The simulation results also reveal a notable trade-off between path safety and efficiency: increasing the obstacle avoidance weight w2 yields safer but longer paths, whereas increasing the goal-reaching weight w1 results in shorter paths at the cost of higher collision risk. Depending on different task requirements, optimal performance metrics can be obtained through proper parameter tuning. Comparative analysis shows that the FESAC algorithm converges significantly faster than standard SAC in complex environments, demonstrating enhanced learning efficiency.
ConclusionThe proposed local observation-based path planning method effectively addresses the challenges posed by limited perception in maritime rescue scenarios, exhibiting strong robustness and adaptability to uncertain environments. By decomposing complex global planning tasks into manageable local subtasks and enhancing feature extraction capabilities, the method provides a practical solution for real-world USV operations where complete environmental information is unavailable. This work provides valuable technical insights for the practical application of reinforcement learning algorithms in actual engineering scenarios.
-
0. 引 言
随着海上贸易的日益繁荣,海上运输活动愈发频繁,船舶碰撞、触礁等安全事故发生频率随之上升,对海上应急搜救的时效性、专业性及资源储备等方面提出了更高要求。传统搜救手段因反应速度慢、人力成本高等局限,常错过搜救“窗口期”。无人艇凭借其灵活性、机动性和高效性,可有效弥补这些不足。路径规划作为无人艇智能航行的关键技术,对确保其在复杂环境中的安全高效搜救至关重要[1-5]。但在沉船搜救这种复杂任务中,任务范围广阔且遍布障碍物,导致环境不确定性较高,而无人艇的局部感知范围难以覆盖全局,并且其有限的感知与决策能力也难以保证任务执行时的稳定性和高效性。因此,如何在任务范围广且不确定性较高的环境中,仅基于局部感知信息进行有效避障和执行海上搜救任务,成为当前无人艇研究中亟待解决的关键问题[6-8]。因此,本研究将针对这一挑战,探讨无人艇如何在海上搜救中,利用局部信息感知完成高效且稳定的路径规划任务,以期为未来无人艇长时间高效作业提供理论支持与技术保障。
针对无人艇路径规划问题,国内外学者已开展了广泛的研究,当前该领域的研究主要可分为2个方向——基于已知环境信息的静态场景下的全局路径规划和基于局部感知的实时决策路径规划。在全局路径规划方面,诸如A*算法[9]和快速扩展随机树[10]等经典算法已被广泛应用。这些算法在路径优化和计算效率方面具有优势,尤其适用于已知环境的静态场景。但是这些方法通常假设环境为静态,且需要获取全局的环境信息,因此在实际的复杂不确定环境中,鲁棒性和适应性较差[11]。在局部路径规划领域,许多基于传感器数据的实时决策算法,如人工势场[12]、动态窗口法[13]等,已被广泛研究并应用。这些算法能够在一定程度上应对不确定环境中的避障问题,但通常依赖专家经验,特别是在大规模随机障碍环境中,往往容易陷入局部最优解,导致避障效果不理想[14]。此外,基于势场法、规则树、概率树等模型的算法虽然能够在某些情况下提供有效的路径规划策略,但往往忽视了船舶的特殊运动特性。例如,船舶具有较强的惯性和较弱的动力系统,且其动力响应较慢,这使得基于简化模型的算法在复杂航行环境中的鲁棒性较差[15]。
近年来,人工智能的迅猛发展为研究人员提供了新的思路,尤其在复杂不确定场景下的路径规划方面,强化学习方法因其特有的自适应学习能力而成为研究的热点。较强的鲁棒性和实时性使得其在无人艇路径规划中展现出显著的优势,尤其适用于复杂不确定环境中的实时决策问题[16]。例如,Guan等[17]提出的基于强化学习的船只避碰决策模型,结合了国际海上避碰规则,其在多船路径规划场景中的灵活性与合规性也通过了模拟验证。为提高无人艇在复杂海况下的避碰决策能力,Wu等[18]基于深度强化学习与动态窗口算法,提出海上自主船只路径规划策略,通过改进近端策略优化算法中的动作选择和奖励函数,显著增强了算法在复杂动态环境中的性能。聚焦微机器人群体动态避障控制,Liu等[19]设计三级雷达系统并通过多次模拟实验验证了其方法在群体避障任务中的有效性,为无人艇多目标避障提供了参考。在动态障碍物环境下的路径规划性能优化方面,Yang等[20]通过强化学习参数更新与探索策略的优化,显著提升避碰效率,并通过复杂气象条件的模拟验证了其实用潜力。Sun等[21]提出一种自组织合作追踪策略,结合Apollonius圆与人工势场方法,优化无人艇群体在复杂环境中的路径规划效率,并提高了对逃避目标的追踪能力。
上述研究尽管取得了一定进展,但主要针对的是特定场景的训练和优化,而在面对海上搜救任务时,由于任务范围广且环境不确定性较高,会导致无人艇感知范围受限,因此直接应用于无人艇路径规划将有诸多挑战。比如,由于状态空间过大和稀疏奖励的存在,强化学习模型在这些复杂场景中往往难以在短时间内达到收敛[22]。此外,基于局部信息的避障算法在复杂、未知环境中也难以顾及长期任务对决策的影响,很难在实际海上搜救任务中达到预期的应用效果。
针对上述问题,本文将基于局部状态感知提出一种深度强化学习无人艇路径规划方法,以解决无人艇在仅依赖局部感知的情况下完成海上搜救任务的难题。首先,为提升算法在随机障碍环境中的鲁棒性,本文将采用SAC(soft actor−critic)算法设计基于局部感知的奖励函数,以解决鲁棒路径规划问题。其次,还将结合特征增强训练方法,提出一种特征增强SAC(feature enhanced soft actor−critic, FESAC)算法,通过提取环境中的关键特征,在小规模特征环境中进行针对性训练,以有效加速算法收敛,提升模型在不确定环境中的学习效率与适应能力。接着,还将针对海上搜救的长期任务中局部规划与全局规划的矛盾,设计基于局部感知域的迭代航路点规划方法,通过感知局部环境信息动态规划航路点,将长期路径规划任务分解为一系列短期鲁棒的避障子任务,从而提升路径规划的决策效率与可行性。最后,将通过仿真实验验证所提方法的有效性。
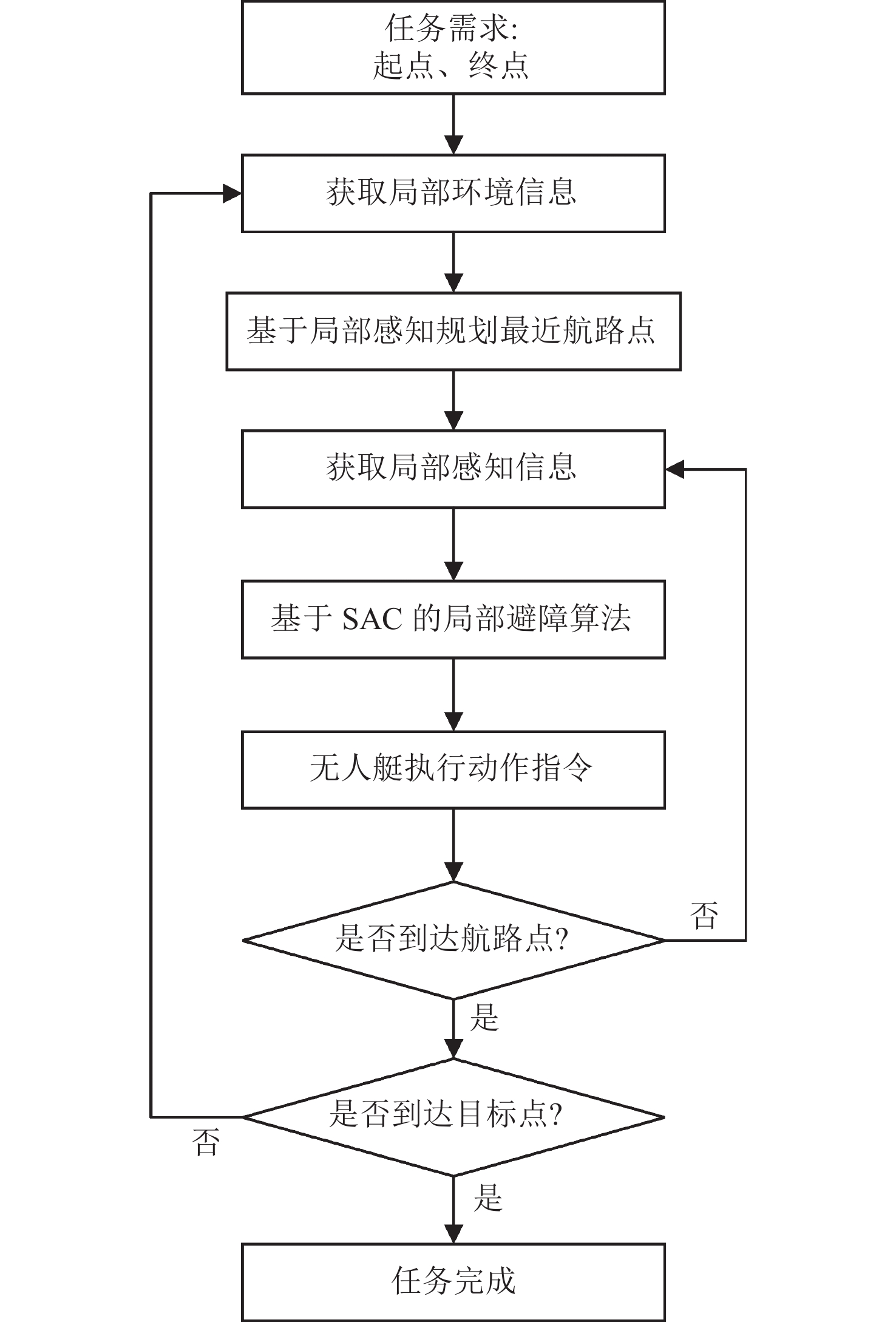
无人艇路径规划方法整体框架如图1所示。
1. 问题描述
1.1 无人艇数学模型
在路径规划中,使用考虑运动学约束的船舶模型而非简单的质点模型,能够显著提升规划结果的实际性和可行性。运动模型能够描述船舶运动的方向性和转弯半径等约束,从而生成更符合实际操控能力的路径。无人艇在实际航行中无法像质点模型假设的那样瞬时到达目标位置或进行无限制的转向,通过对这些限制的建模,可以避免规划出不切实际的路径。此外,运动学模型有助于提高路径的平滑性和可操作性,尤其在需要频繁转向的复杂环境中,可以避免急转弯等导致无人艇无法执行的情况。
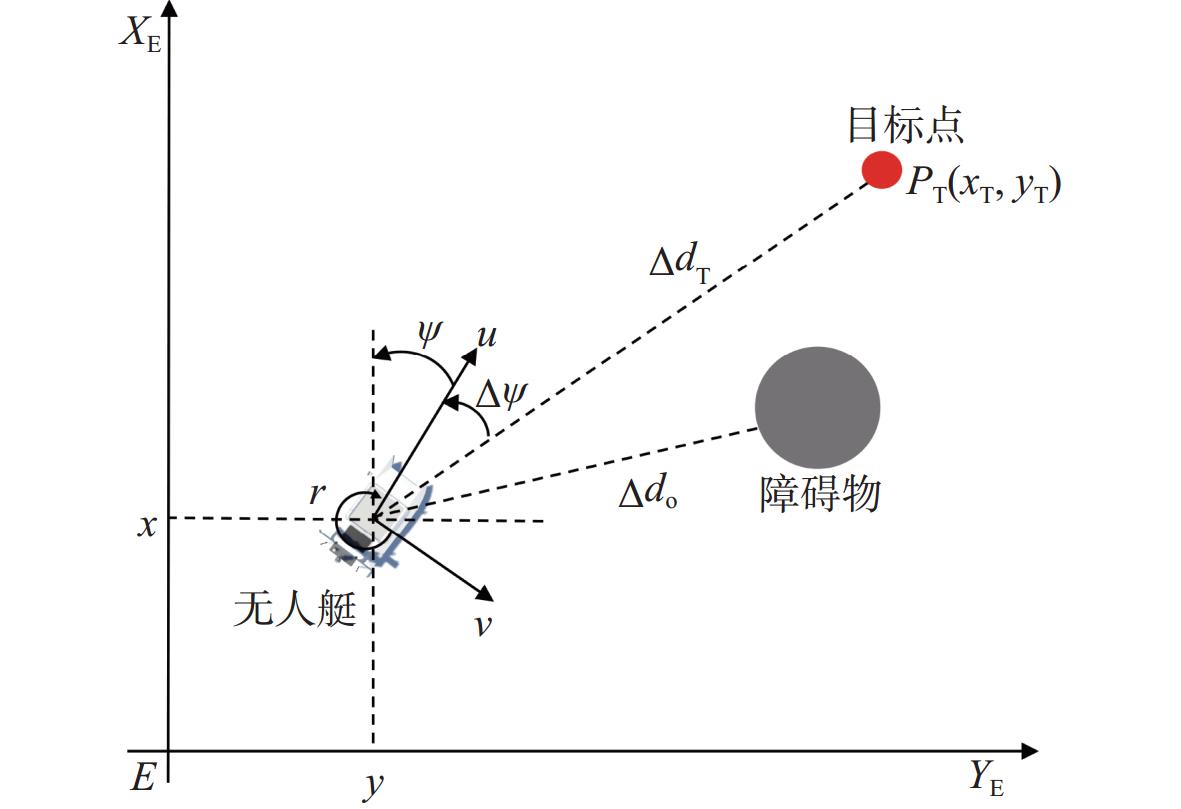
在海上搜救任务中,环境中存在大量随机障碍物,无人艇模型的物理约束能有效防止路径规划出现过于激进的转向或速度变化,提高路径的平滑性和可操作性。此外,运动学模型为实时导航和控制系统提供了更可靠的路径规划基础,可与自动控制算法配合使用,确保路径的可实现性和稳定性。本文建立三自由度无人艇数学模型来研究欠驱动无人艇路径规划问题,如图2所示。
其中:x,y,ψ分别为无人艇在地球固定坐标系中的位置坐标和艏揺角;u,v,r分别是无人艇在船体坐标系中纵向速度、横向速度和艏揺角速度;Δψ为无人艇与目标点的航向偏差;ΔdT为无人艇到目标点的距离;Δdo为无人艇到障碍物的距离。
无人艇的运动学模型可以表示为
\left\{ \begin{aligned} & {\boldsymbol{\dot \eta = R}}(\psi ){\boldsymbol{\upsilon }} \\ & {\boldsymbol{M\dot \upsilon = \tau }} - {\boldsymbol{C}}({\boldsymbol{\upsilon }}){\boldsymbol{\upsilon }} - {\boldsymbol{D}}({\boldsymbol{\upsilon }}){\boldsymbol{\upsilon }} \end{aligned}\right. (1) 式中:位姿向量 {\boldsymbol{\eta }} = {\left[ {x,y,\psi } \right]^{\text{T}}} ;速度向量 {\boldsymbol{\upsilon }} = {\left[ {u,v,r} \right]^{\text{T}}} ; {\boldsymbol{\tau }} = {\left[ {{\tau _u},0,{\tau _r}} \right]^{\text{T}}} 为无人艇控制输入,包括纵向推力和转艏力矩; {\boldsymbol{R}}(\psi ) 为旋转矩阵;M为惯性矩阵; {\boldsymbol{C}}({\boldsymbol{\upsilon }}) 为科里奥利力和向心力矩阵; {\boldsymbol{D}}({\boldsymbol{\upsilon }}) 为水动力阻尼矩阵。
1.2 SAC强化学习算法
无人艇路径规划的过程可以建模为一个强化学习问题。其中,无人艇通过与环境交互,在每个时间步从环境中获取一个状态 {{\boldsymbol{s}}_t} ,在采取动作 {{\boldsymbol{a}}_t} 后转移到下一个状态 {{\boldsymbol{s}}_{t + 1}} ,并获得奖励 {R_t} 。在这一过程中,无人艇的决策过程必须遵循策略 \pi \left( {{{\boldsymbol{a}}_t}\left| {{{\boldsymbol{s}}_t}} \right.} \right) ,即基于当前状态选择相应动作的概率分布。该过程可建模为一个马尔可夫决策过程,用五元组 \left\langle {{\mathcal{S}},{\mathcal{A}},P,R,\gamma } \right\rangle 表示,其中 {\mathcal{S}} 为状态空间,表示无人艇在环境中可能的所有状态集合; \mathcal{A} 为动作空间,表示无人艇能够采取的所有可能动作集合;R为奖励函数,定义状态和动作对的奖励值,即 {R_t}({{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t}) ;P为状态转移概率,描述无人艇在采取动作 {{\boldsymbol{a}}_t} 后从当前状态 {{\boldsymbol{s}}_t} 转移到下一状态 {{\boldsymbol{s}}_{t + 1}} 的概率,即 p\left( {{{\boldsymbol{s}}_{t + 1}}\left| {{{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t}} \right.} \right) \in \left[ {{\text{0,1}}} \right] ; \gamma 是折扣因子,表示未来奖励的重要性。在强化学习框架下,路径规划目标是通过最大化累积奖励学习最优策略 {\pi ^*} ,即
{\pi ^*} = \arg {\max _\pi }\mathbb{E}\left[ {\sum\limits_{t = 0}^T {{\gamma ^t}} {R_t}({{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t})} \right] (2) 通过优化策略 \pi ,无人艇能够在复杂海洋环境下生成能够有效避障的最优动作序列,同时满足运动学和物理约束。
与传统强化学习算法不同,SAC算法的核心思想是结合最大化累积回报和增加策略的随机性,通过在优化目标中引入熵项,使其在学习高奖励策略的同时,保留一定的探索性。这种方法可以避免过早收敛到局部最优策略,提高路径规划在不确定环境中的适应能力和全局性。SAC算法的优化目标被扩展为
J(\pi ) = {\mathbb{E}_{\tau ~\pi }}\left[ {\sum\limits_{t = 0}^\infty {{\gamma ^t}} {R_t}({{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t}) + \alpha H(\pi ( \cdot |{{\boldsymbol{s}}_t}))} \right] (3) 式中: J(\pi ) 是优化目标; \tau 是由策略 \pi 生成的轨迹; H(\pi ( \cdot |{{\boldsymbol{s}}_t})) = - {\mathbb{E}_{\tau ~\pi }}\left[ {\log \pi ( \cdot |{{\boldsymbol{s}}_t})} \right] 是策略在状态 {{\boldsymbol{s}}_t} 下的熵,表示在策略 \pi 下可能输出的不同动作的探索程度; \alpha 是温度参数,用于平衡回报和熵的权重。
SAC算法采用Actor−Critic架构来分别处理策略学习和价值估计。其中Actor网络负责生成策略,参数为\phi ;Critic网络用于评估策略的质量,包括状态价值网络{V_\psi }、目标状态价值网络{V_{\psi '}}以及2个动作价值网络{Q_{{\theta _1}}}和{Q_{{\theta _2}}},\psi 和\theta 是其网络参数。目标状态价值函数的目的是引入稳定性,避免过快更新导致训练不稳定,使用2个Q网络可以解决Q值过高的估计问题,并通过选取最小的Q值来更新策略。
在网络参数更新时,Critic网络的目标是最小化时序差分误差。其中,动作价值网络的损失函数表示为
{L_Q}({\theta _i}) = {\mathbb{E}_\mathcal{D}}\left[ {\frac{1}{2}{{(\hat Q({{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t}) - {Q_{{\theta _i}}}({{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t}))}^2}} \right] (4) 式中:\hat Q({{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t}) = {R_t}({{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t}) + \gamma {V_{\psi '}}({{\boldsymbol{s}}_{t + 1}});i \in \left\{ {1,2} \right\}用于选择2个Q网络之一进行更新;\mathcal{D}表示经验回放池。
状态价值网络通过最小化Q值和状态价值的差异来更新价值函数,其损失函数表示为
\begin{split} & {L_V}(\psi ) = {\mathbb{E}_\mathcal{D}}\left[ {\frac{1}{2}\left( {{V_\psi }({{\boldsymbol{s}}_t}) - {{\min }_{i = 1,2}}{Q_{{\theta _i}}}({{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t}) - } \right.} \right. \\ &\qquad\qquad \left. {{{\left. {\alpha \log {\pi _\phi }({{\boldsymbol{a}}_t}|{{\boldsymbol{s}}_t})} \right)}^2}} \right] \end{split} (5) 为确保更新过程的稳定性,目标状态价值网络通过软更新\psi ' = \sigma \psi + (1 - \sigma )\psi '实现参数调整,其中\sigma 为软更新系数。
Actor网络的目标是通过最大化奖励和熵来选择最优的动作,损失函数表示为
{L_\pi }(\phi ) = {\mathbb{E}_\mathcal{D}}\left[ {\alpha \log {\pi _\phi }({{\boldsymbol{a}}_t}|{{\boldsymbol{s}}_t}) - {{\min }_{i = 1,2}}{Q_{{\theta _i}}}({{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t})} \right] (6) 式中,{\min _{i = 1,2}}{Q_{{\theta _i}}}({{\boldsymbol{s}}_t},{{\boldsymbol{a}}_t})是Critic网络2个动作价值函数中的最小值。
温度参数\alpha 控制着熵项的权重,可以通过以下损失函数进行更新:
L(\alpha ) = {\mathbb{E}_\mathcal{D}}\left[ { - \alpha \log {\pi _\phi }({{\boldsymbol{a}}_t}|{{\boldsymbol{s}}_t}) - \alpha {H_0}} \right] (7) 式中,目标是使得策略保持一定的熵水平{H_0},这个值一般设置为常数。
SAC算法使用深度神经网络来近似这些函数,并利用经验回放来存储和采样交互经验,以此训练网络参数。经验回放机制允许算法从过去的经验中学习,在提高数据的利用率同时减少样本之间的相关性。此外,SAC算法温度参数 \alpha 的自适应更新机制可以确保策略的熵在训练过程中保持在合适的水平。通过这种方式,SAC算法能够在复杂海洋环境中有效地平衡探索和利用,从而实现更优的决策和控制,算法框架如图3所示。
2. 基于局部感知的无人艇路径规划方法
2.1 基于局部信息的强化学习模型
2.1.1 状态空间设计
海上搜救任务中,情况复杂多变,难以预测,往往需要无人艇根据局部感知随机应变。本文基于无人艇的局部感知构建状态空间,使用激光雷达感知与周围障碍物的距离、方位等信息,状态空间包括无人艇的位置、速度、相对目标点的相对位置差,以及通过激光雷达观察到的障碍物信息,表述为
\begin{split} &\;\\[-10pt]& {\boldsymbol{s}} = {\left[ {\Delta {d_{\text{T}}},\Delta \varphi ,u,v,r,\Delta {d_{\text{o}}},\Delta \beta } \right]^{\text{T}}} \end{split} (8) 式中: \Delta {d_{\text{T}}} 和 \Delta \varphi 分别表示无人艇位置 P(x,y) 与目标点位置 {P_{\text{T}}}({x_{\text{T}}},{y_{\text{T}}}) 之间的相对距离和航向偏差; \Delta {d_{\text{o}}} 和 \Delta \beta 分别表示雷达传感器检测到的与最近障碍物之间的相对距离和航向偏差,其中, \Delta {d_{\text{o}}} 和 \Delta \beta 由激光雷达直接测得, \Delta {d_{\text{T}}} 表述为
\Delta {d_{\text{T}}} = \sqrt {{{({x_{\text{T}}} - x)}^2} + {{({y_{\text{T}}} - y)}^2}} (9) 航向偏差 \Delta \varphi 计算公式为
\Delta \varphi = {\varphi _{\text{T}}} - {\varphi _t} (10) 式中: {\varphi _t} 为无人艇实时航向; {\varphi _{\text{T}}} 为目标点方位角。
2.1.2 动作空间设计
在无人艇路径规划任务中,动作空间设计的合理性直接决定了算法的学习效率、路径规划精度以及在不确定环境中的适应能力,是确保任务成功完成的关键因素。由于本文使用的是欠驱动无人艇的三自由度模型,其驱动由控制输入 \tau_{\mathrm{c}} 表示,且由于是欠驱动模型,所以 {\tau _v} \equiv 0 。设置动作空间 {\boldsymbol{a}} = {\left[ {{\tau _u},0,{\tau _r}} \right]^{\text{T}}} ,参考文献[8]中的船体数据后,将本文中 {\tau _u} 取值范围确定为[−400 N, 400 N], {\tau _r} 的取值范围为[−20 N, 20 N]。
2.1.3 奖励函数设计
在海上搜救任务中,奖励函数通过为无人艇的行为提供实时反馈,直接引导无人艇在学习过程中采取最优策略。设计合理的奖励函数不仅能够促使无人艇有效避开障碍物,还能优化路径选择,推动无人艇趋向较短、平稳的行驶轨迹,并提升控制行为的精确性。通过平衡探索与利用,奖励函数在强化学习过程中起着至关重要的作用,深刻影响着智能体的学习效率、决策质量以及最终任务的完成效果。
奖励功能由完成奖励、碰撞处罚和过程奖励组成。完成奖励的作用是鼓励无人艇达到目标状态。该奖励需要具有相当大的价值,以确保无人艇尝试完成指定的任务,其在学习过程中提供最直接的反馈。本文中,当无人艇的位置与对应目标点之间的 \Delta {d_{\text{T}}} 距离小于1 m时,认为无人艇的任务已完成,完成奖励定义为
{r_{{\text{finish}}}} = \left\{ \begin{aligned} & {100} &&{\mathrm{if}}\;\Delta {d_{\text{T}}} \leqslant 1\\ & 0 &&{\mathrm{if}}\;\Delta {d_{\text{T}}} > 1 \end{aligned} \right. (11) 碰撞惩罚是无人艇发生碰撞时给予的负奖励。这种惩罚作为一种学习机制,用以避免危险和不安全的行为。本文设定当无人艇与障碍物之间的距离 \Delta {d_{\text{o}}} 小于1 m时,则认为发生碰撞,因此无人艇的碰撞惩罚定义如下:
{r_{{\text{collish}}}} = \left\{ \begin{aligned} & { - 10} &&{\mathrm{if}}\; \Delta {d_{\text{o}}} \leqslant 1\\ & 0 && {\mathrm{if}}\;\Delta {d_{\text{o}}} > 1 \end{aligned} \right. (12) 为避免稀疏奖励问题的产生,需要设计过程奖励机制,为无人艇提供连续且细化的奖励信号,以引导其在实现长期目标的同时专注于短期行动优化。此类奖励机制能够有效增强智能体的探索能力,避免陷入局部最优,并显著提升算法的收敛速度。具体形式通过以下式表述:
{r_{{\text{process}}}} = p(\Delta {d_{{\text{T}},t}} - \Delta {d_{{\text{T}},t - 1}}) (13) 式中:p是奖励系数; \Delta {d_{{\text{T}},t}} 是当前时间步无人艇与相应目标点之间的距离。最后,可以获得总奖励的方程为
{r_{{\text{total}}}} = {r_{{\text{finish}}}} + {r_{{\text{collish}}}} + {r_{{\text{process}}}} (14) 2.2 特征增强训练方法
尽管深度强化学习在避障领域的研究已经取得了显著进展,但在海上沉船搜救这种覆盖范围广、不确定性高的环境中应用时,会由于状态空间过于庞大,样本采样率低,导致强化学习模型的训练效率较低,甚至可能难以收敛至可用的策略。此外,在避障过程中,无人搜救船通常只能依赖局部感知信息进行决策,这进一步增加了任务的复杂性。基于上述问题,本文认为通过对任务特征进行提炼,可以将全局路径规划问题建模为一系列连续的局部避障过程。所以在此基础上,结合SAC算法与特征增强训练方法,提出了FESAC算法,以提高模型的训练效率及其对不确定环境适应能力,伪代码如表1所示。该方法的核心思想是通过构建小规模特征环境,随机布置少量障碍物,并在每个训练回合中随机重置障碍物、无人艇以及目标点的位置,让无人艇仅依赖局部感知信息执行避障任务。通过这种方式,模型能够在较短时间内高效地学习应对不同障碍物场景的鲁棒控制策略,从而提高其在不确定环境中的泛化能力和适应性。表2为训练时各项超参数的设置。
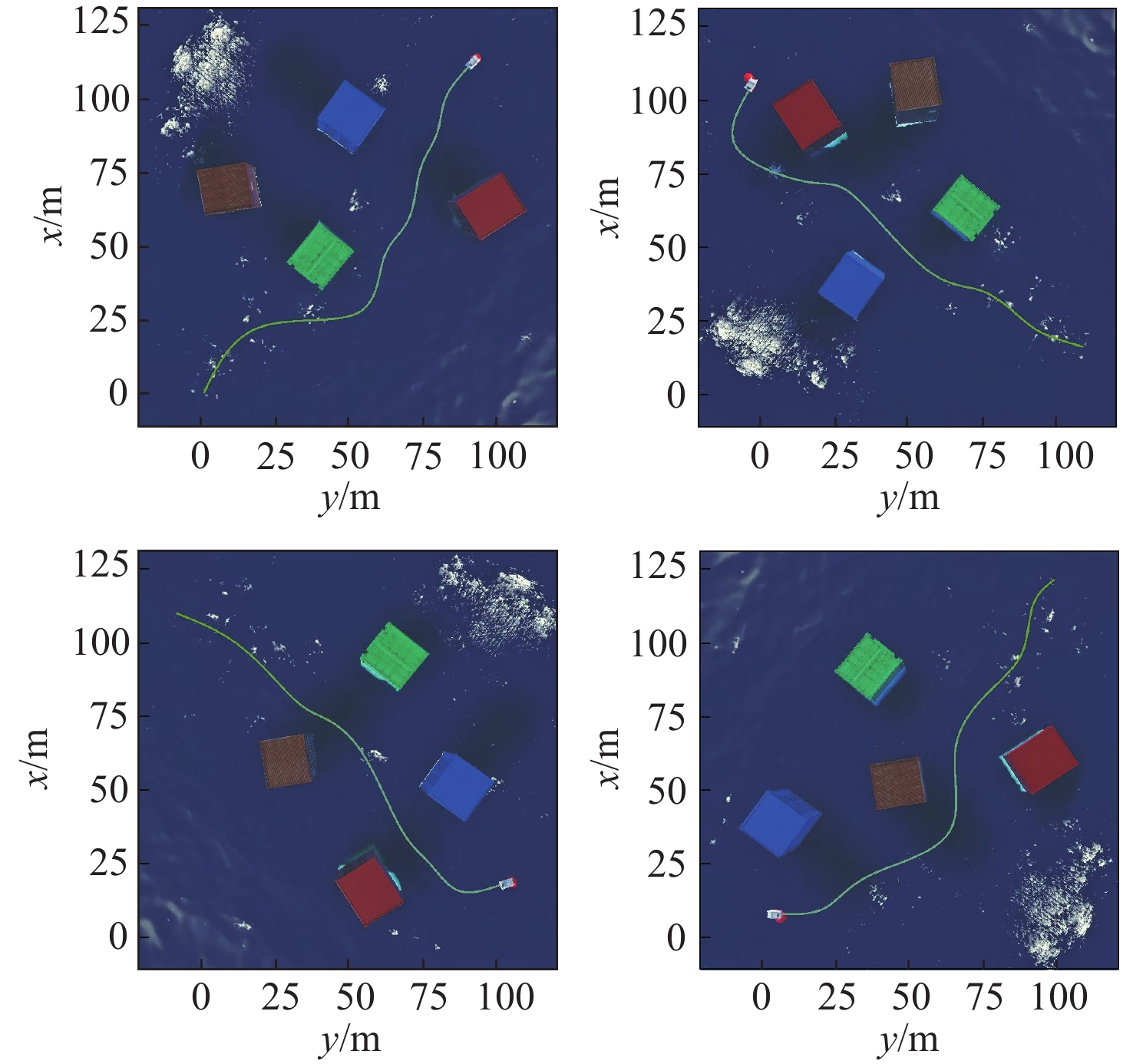
表 1 FESAC算法伪代码Table 1. Pseudo-code of FESAC algorithm算法1:FESAC算法 输入:网络参数\phi ,\psi ,\psi ',{\theta _1},{\theta _2} 1: 初始化网络参数\phi ,\psi ,\psi ',{\theta _1},{\theta _2},创建经验回放池\mathcal{D},建立特征增强随机特征环境 2: for 训练周期e = 1,2,...,E do: 3: 初始化环境状态{s_0},设置索引{d_0} = 0 4: for 时间步t = 1,2,...,T do: 5: 获取状态{s_t}并采样获得动作{a_t} \sim {\pi _\phi }( \cdot |{s_t}) 6: 获取奖励{r_t}、状态{s_{t + 1}}和索引{d_t} 7: 将({s_t},{a_t},{r_t},{s_{t + 1}},{d_t})存储到经验回放池\mathcal{D} 8: if t = T,开始训练网络: 9: for 训练轮次k = 1,2,...,K do: 10: 从\mathcal{D}中随机采样m组数据: 11: 更新网络参数: {\theta _1} \leftarrow {\theta _1} - \lambda {\nabla _{{\theta _1}}}{L_Q}({\theta _1}) {\theta _2} \leftarrow {\theta _2} - \lambda {\nabla _{{\theta _2}}}{L_Q}({\theta _2}) \psi \leftarrow \psi - \lambda {\nabla _\psi }{L_V}(\psi ) \psi ' \leftarrow \sigma \psi + (1 - \sigma )\psi ' \phi \leftarrow \phi - \lambda {\nabla _\phi }{L_\pi }(\phi ) \alpha \leftarrow \alpha - \lambda {\nabla _\alpha }L(\alpha ) 12: end for 13: else 14: 继续与环境交互 15: end if 16: end for 17: end for 表 2 FESAC超参数设置Table 2. Hyperparameter configuration of FESAC algorithm参数 值 折扣因子\gamma 0.99 学习率\lambda 0.001 批次大小 256 经验池容量 1 000 000 优化器 Adam 图4所示是4个100 m×100 m的特征环境下的路径规划结果,其中障碍物、无人艇以及目标点的位置在每次实验中均随机生成。由于在决策过程中仅依赖局部感知信息,所以生成的路径并非是全局最优解,但所规划的路径仍表现出较高的效率,能够在较短的距离内完成任务目标。为验证算法的鲁棒性,本文在算法收敛后随机生成100组测试数据,以评估模型的稳定性。实验结果表明,该方法在测试数据中的任务成功率达到98%,验证了其可靠性和适应性。
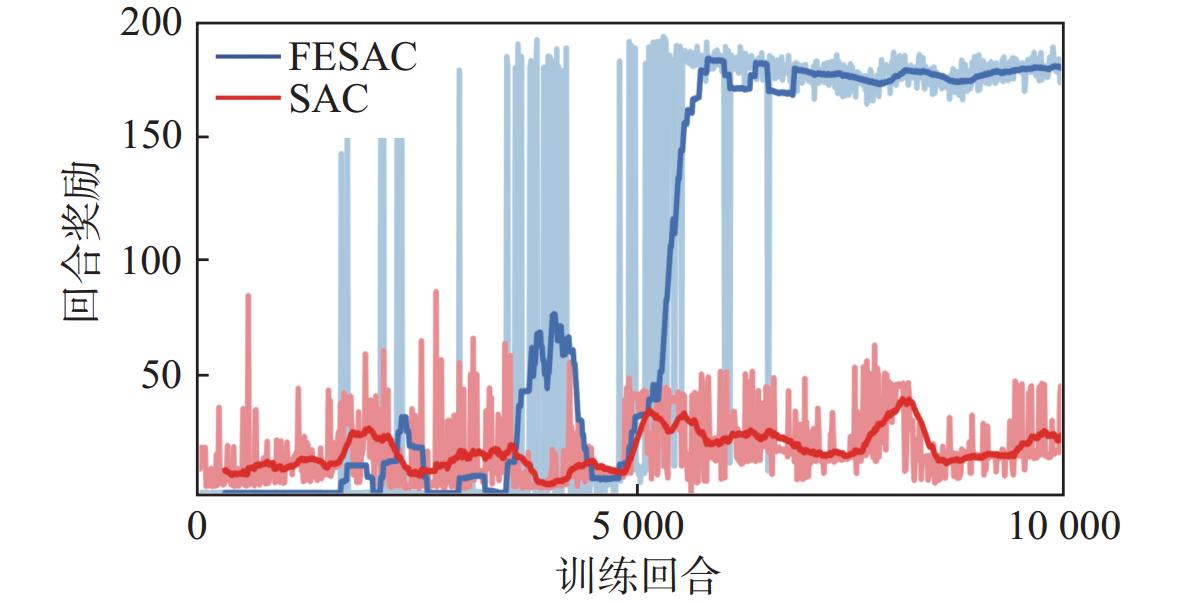
图5对比了在随机场景下采用FESAC算法进行训练的奖励反馈,以及在全局环境中直接使用SAC算法进行避障训练回合的奖励反馈。从图中可以观察到,直接在全局环境中训练SAC算法时,由于状态空间较大,不仅训练速度显著降低,而且最终难以实现收敛。这表明传统方法在状态空间较大且有随机障碍的环境中的表现受到显著限制。相比之下,采用特征增强算法的FESAC方法不仅显著加快了训练过程,还能实现稳定的收敛效果。这一结果说明,特征增强算法通过将全局问题分解为一系列局部问题,可有效降低状态空间的复杂性,提高训练效率和模型的适应性,验证了其在复杂避障任务中的实际应用潜力。
该方法不仅有效降低了训练环境复杂性,还通过强化局部感知能力,提高了对全局任务的适应性,展现出其在高不确定性环境中的广泛应用前景,为复杂任务的分解与高效训练提供了一种创新性思路,尤其在资源受限或对实时性要求较高的场景中,具有重要的实用价值和潜在意义。
2.3 基于局部感知域的迭代航路点规划
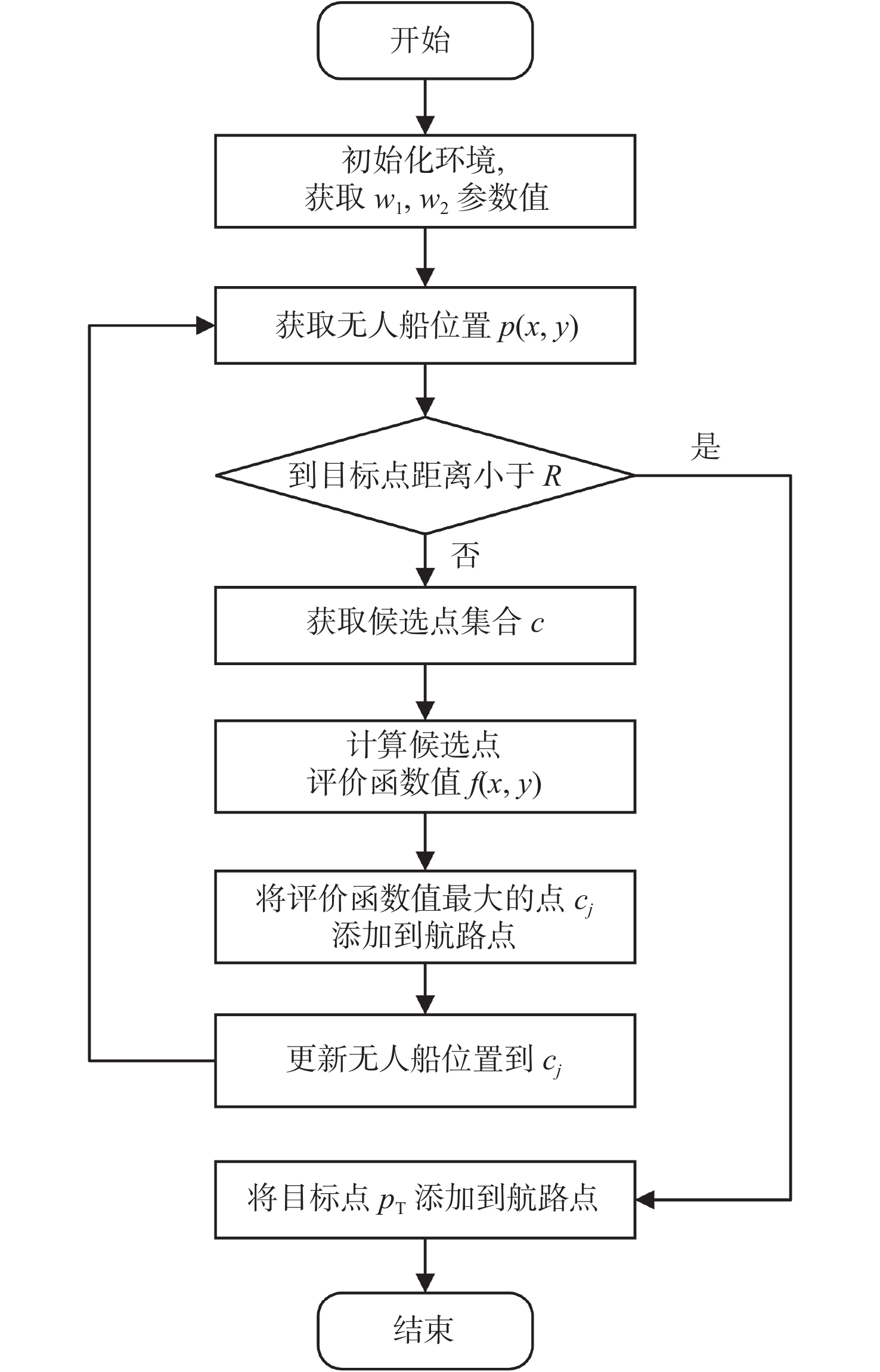
为实现FESAC算法在全局环境下的路径规划,本文还提出一种基于局部感知域的航路点规划方法。该方法的核心思想是通过引入航路点,将全局环境中的长期路径规划任务分解为多个与特征增强训练模型相匹配的短期路径规划子任务。在航路点规划中,无人艇需要从当前位置规划到下一个航路点的路径。这一路径规划任务可以视为一个短期的小规模路径规划问题,与FESAC算法训练时所使用的特征环境高度契合。FESAC算法通过提取环境关键特征并在随机特征环境中训练,提升了无人艇在局部感知条件下的避障和路径规划能力。因此,FESAC算法可直接应用于这些短期子任务,为无人艇提供高效的避障和路径规划支持。通过将长期全局路径规划任务分解为一系列短期子任务,并利用FESAC算法解决每个子任务,本方法能够在有限感知条件下有效实现全局路径规划,同时克服局部感知的局限性。
在实际的海上搜救任务中,由于无人艇感知范围有限且环境不确定性较高,全局信息的获取往往存在较大难度。因此,本文创新性将局部感知域应用到航路点规划过程之中。在具体实现中,无人艇首先根据航路点完成当前阶段的路径规划任务,当抵达当前航路点后,再基于局部感知信息动态确定下一阶段的航路点,依此迭代,直至最终抵达目标点。
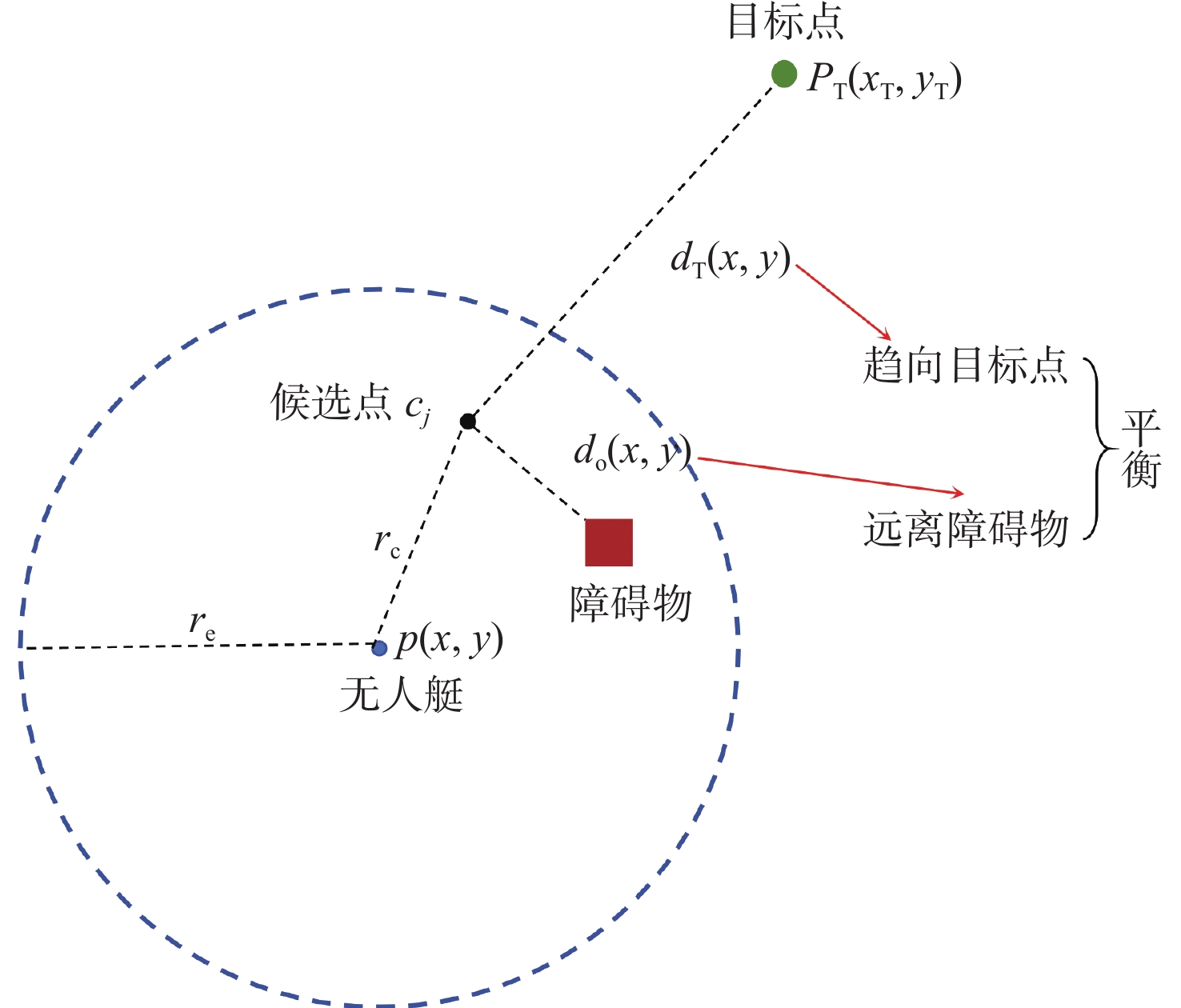
航路点选择可以视为一个优化问题,如图6所示。其中, {r_{\text{e}}} 为无人艇感知范围,候选点 \mathcal{C} = \left\{ {{{\boldsymbol{c}}_1},{{\boldsymbol{c}}_2}, \ldots ,{{\boldsymbol{c}}_m}} \right\} 分布在以无人艇位置为圆心,半径为 {r_{\text{c}}} 的圆周上,其坐标为 {{\boldsymbol{c}}_j} = {\boldsymbol{p}} + {r_{\text{e}}} \cdot (\cos {\theta _j},\sin {\theta _j}), {\theta _j} \in [0,2{\text{π }}],j = 1,2, \ldots ,m ,其中 {\boldsymbol{p}} = {[x,y]^{\text{T}}} 为无人艇的位置向量,m为候选点的数量,对每个候选点进行迭代,最终选择评分函数值最大的候选点。为避免候选点与感知范围外的障碍物相距太近,取 {r_{\text{c}}} = 0.75{r_{\text{e}}} 。当目标点处于感知范围时,直接将目标点加入路径。本文采用加权目标函数:
f(x,y) = - {w_1} \cdot \Delta {d_{\text{T}}}(x,y) + {w_2} \cdot {d_o}(x,y) (15) 式中: {d_{\text{T}}}(x,y) 和 d_{\mathrm{o}}(x,y) 分别是候选点距离目标点和最近障碍物的距离, \Delta {d_{\text{T}}}(x,y) 表示当前候选点跟目标点间距离与最短距离间的差值; {w_1} 和 {w_2} 是权重参数,目标函数通过调整 {w_1} 和 {w_2} 的值,可动态平衡趋近目标点与远离障碍物。增大 {w_2} 的值,优先远离障碍物;减小 {w_1} 的值,稍微放缓接近目标点的优先级。
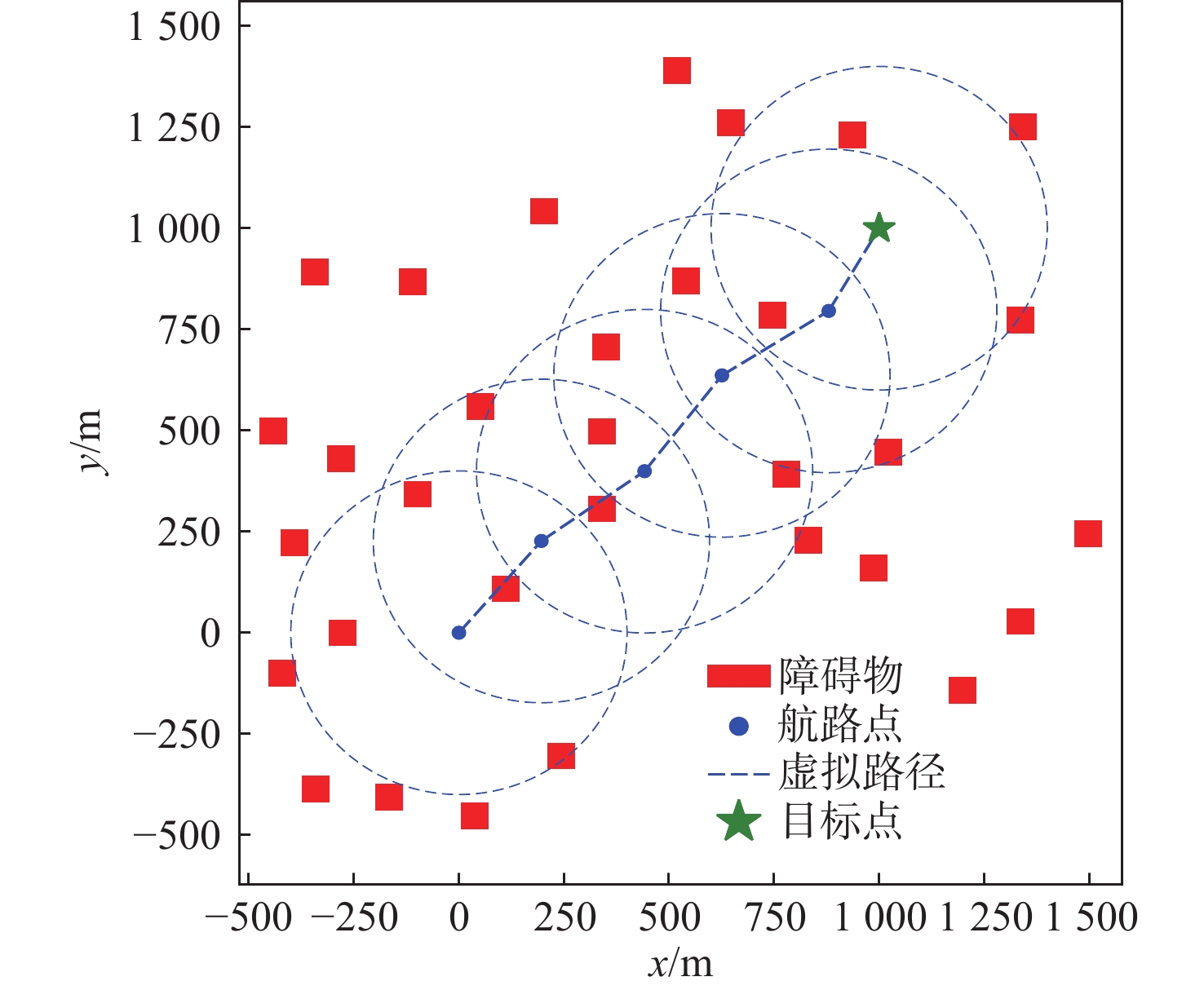
规划过程如图7所示,在随机障碍物环境下规划出的航路点见图8,其中绿星代表目标点,蓝色点为选定航路点,障碍物威胁半径设定为5 m。取{w_1} = - 1, {w_2} = 1。可以看到,在该参数取值条件下,所规划的航路点能够有效平衡向目标点趋近的轨迹优化与避障要求,从而保证航路点在趋近目标的过程中能有效避开障碍物。
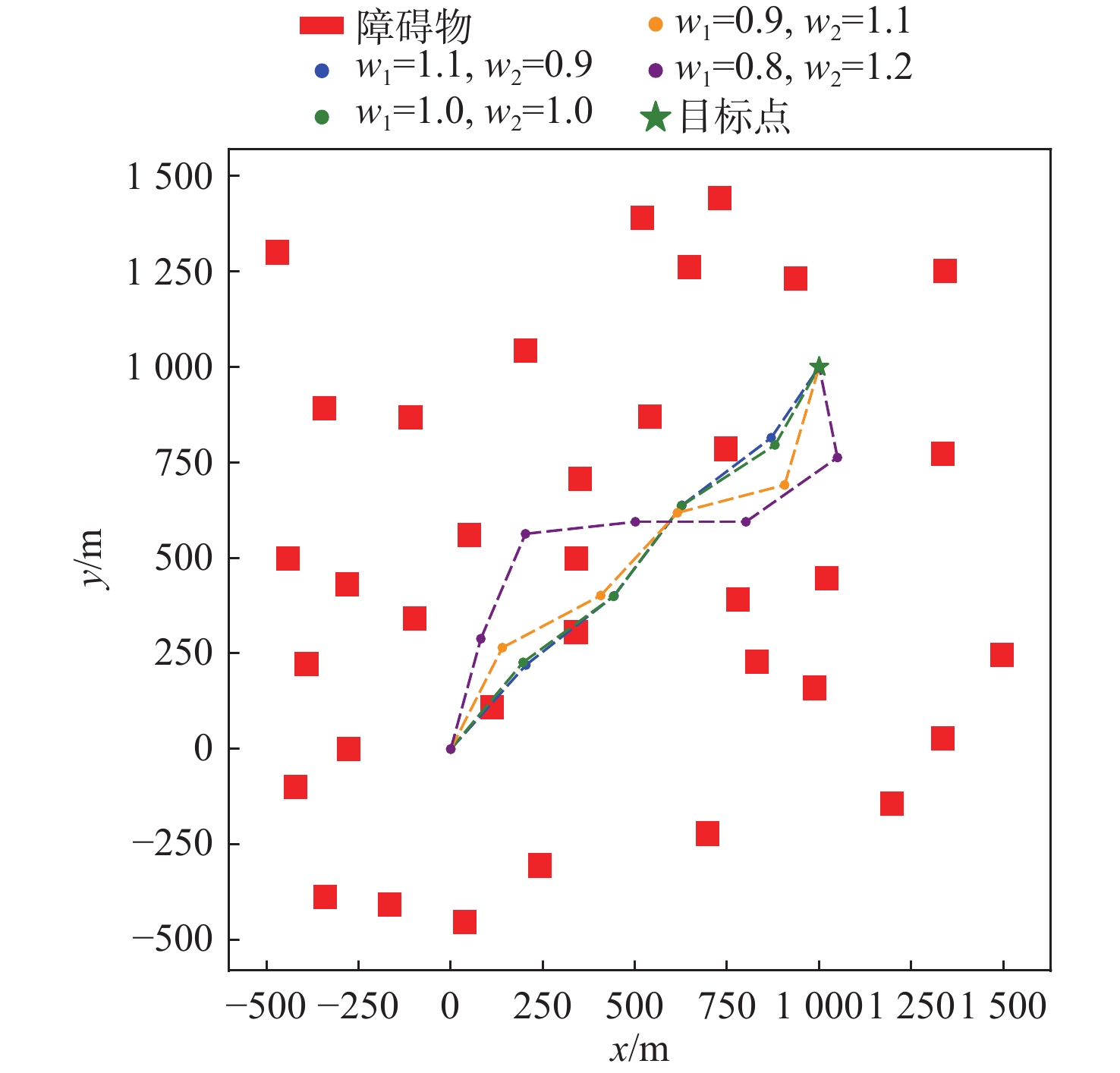
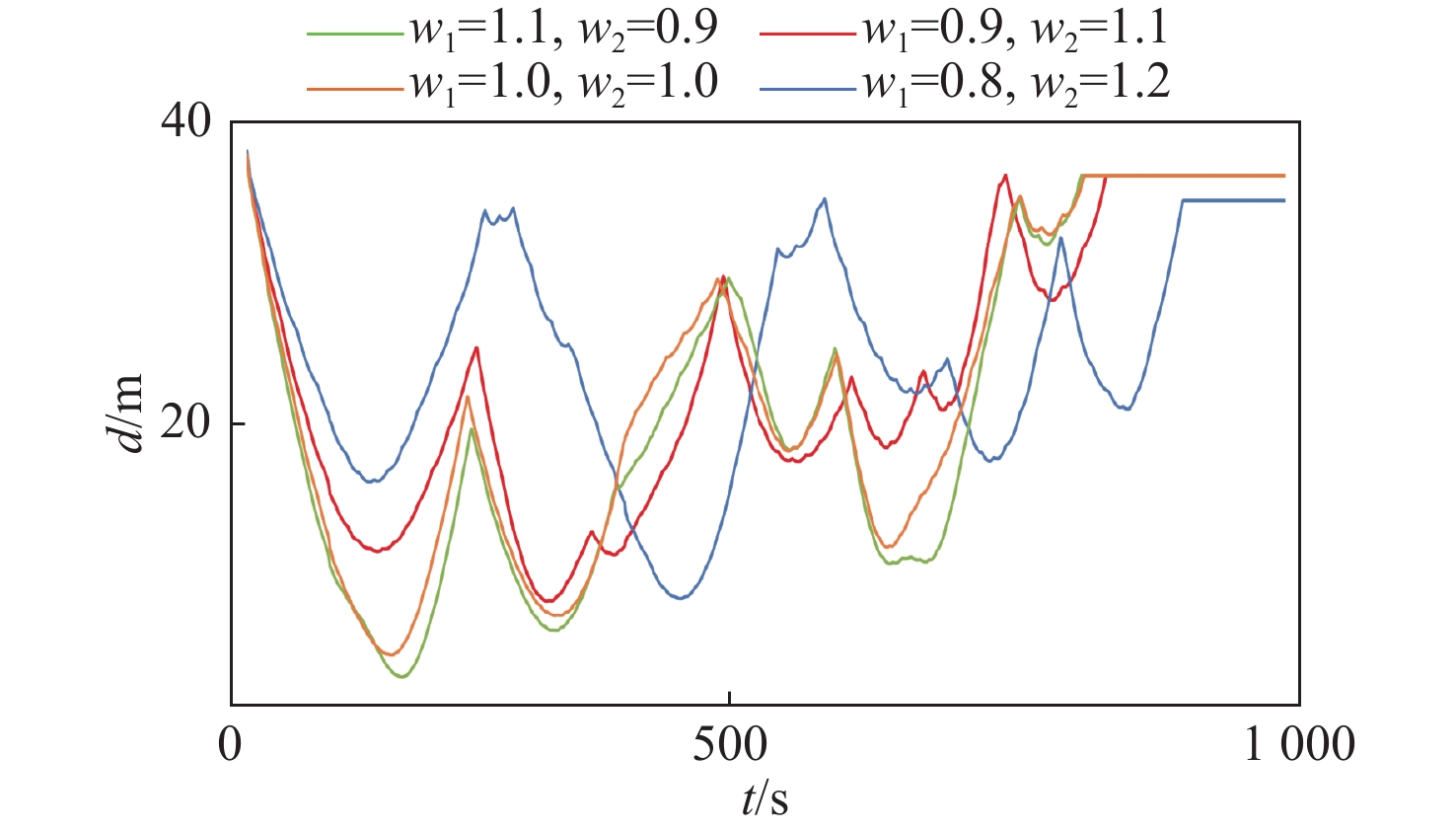
为验证不同参数的取值对最终规划出的航路点的影响,本文在同一随机环境下取4组不同的值进行实验,结果如图9所示,可以看到,随着 {w_1} 增大,所选定的航路点更趋近于无人艇与目标点的连线上;而增大 {w_2} 的值则会使得航路点尽量远离障碍物,但随之也会导致总体规划更加远离最近路径,路线也更为曲折。
3. 仿真验证
为验证所提出算法的有效性,本文基于Unity3D虚拟引擎搭建了海上搜救任务仿真平台。本仿真环境主要模拟了随机分布的静态障碍物(如散落集装箱),但未考虑气象条件(如风、浪、流)等动态环境因素的影响。这种简化对其在真实海况中的直接适用性有一定影响,但使模型能够专注于路径规划算法的验证。如图10所示,该仿真场景以侧倾沉没的运输船引发的海上搜救任务为背景,仿真范围为1 000 m×1 000 m,模拟了大范围海域中散落集装箱形成的随机障碍物分布。每轮实验中,障碍物数量在20~50个之间随机生成,位置随机分布于场景内。无人艇采用三自由度欠驱动模型,配备激光雷达传感器,感知范围为100 m,扫描角度360°,分辨率为10°,可实时检测障碍物的距离和方位。实验中,无人艇初始位置设为(0 m, 0 m),目标点位于(1 000 m, 1 000 m)。仿真参数汇总见表3。
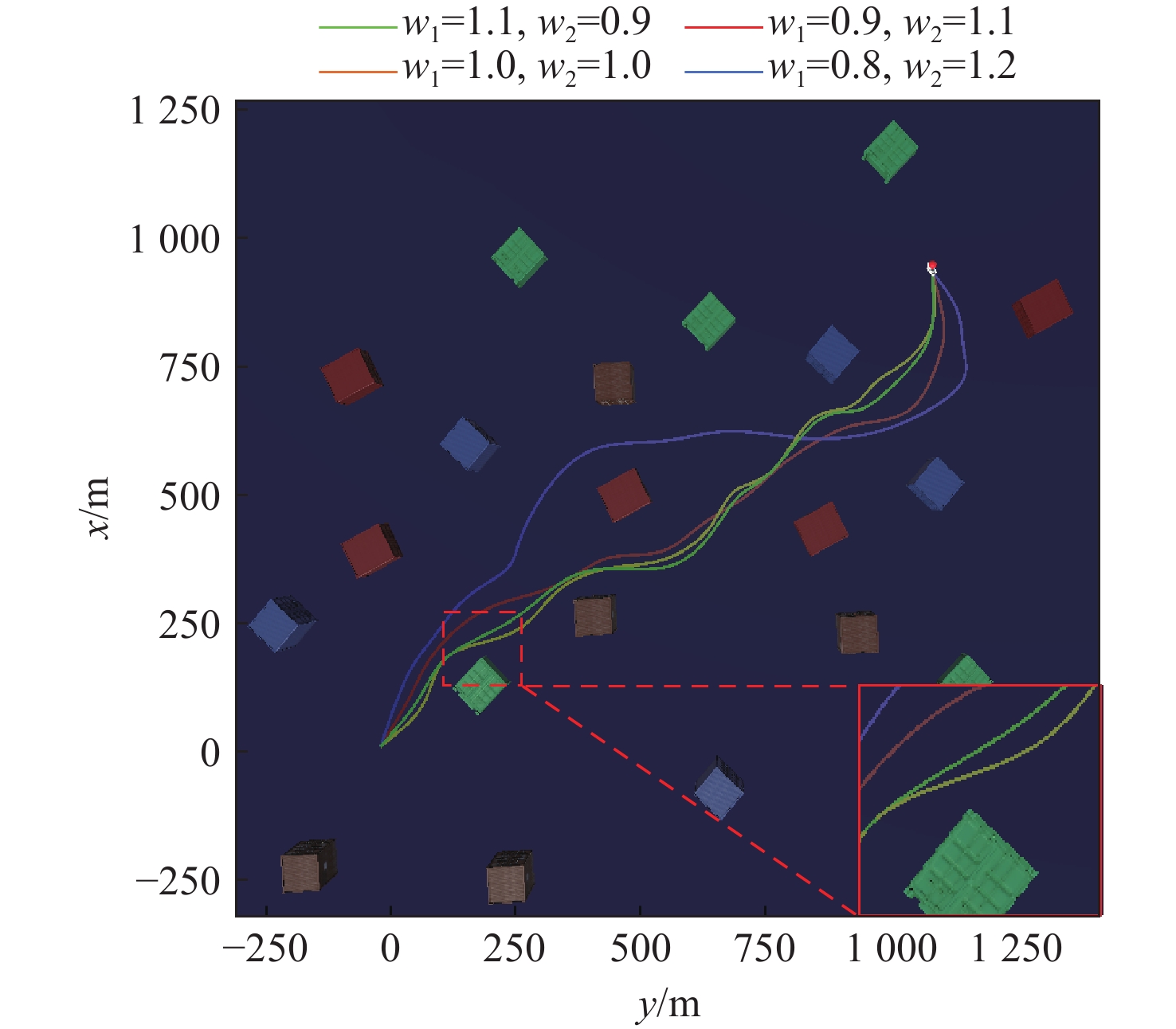
表 3 仿真参数Table 3. Simulation parameters参数类别 参数名称 值 运动学参数 {\tau _u} [−400 N, 400 N] {\tau _r} [−20 N, 20 N] 奖励函数参数 p 1.0 航路点规划参数 {r_{\text{e}}} 100 m {r_{\text{c}}} 75 m m 360 图11和图12显示了在不同的{w_1}和{w_2}参数设置下无人艇的路径呈现出的不同特征。随着{w_2}的增大,航路点选择更注重避开障碍物,路径与障碍物的平均距离增加,提高了路径安全性但导致路径长度延长,到达目标点的时间显著增加,效率降低。相反,增大{w_1},航路点选择更倾向于接近目标点,缩短路径长度,但导致航路点与障碍物距离减小,无人艇与障碍物距离过近,碰撞风险上升。
接下来,进一步分析成功率与路径长度的关系。在对多组参数进行100组随机实验后,结果如表4所示。当{w_1}较大时,路径规划倾向于选择较短的路径以减少到达目标的时间和路径长度。然而,由于这种路径选择的航路点与障碍物的距离较近,导致路径的复杂化,从而增加了避障的难度,无人艇在避障过程中可能需要较大的转向角度来规避障碍物,使得成功率显著下降。反之,增大{w_2}时,路径更注重避障,航路点与障碍物距离增加,成功率提高,但路径长度显著延长,效率下降。
表 4 不同参数下路径规划结果Table 4. Path planning results under different parameters策略 {w_1} {w_2} 路径长度/m 成功率/% #1 0.8 1.2 1 721.3 93 #2 0.9 1.1 1 574.7 90 #3 1.0 1.0 1 534.6 80 #4 1.1 0.9 1 535.2 72 #5 1.2 0.8 1 576.4 65 从实验数据中可以看出,{w_1}和{w_2}的选择对路径规划的安全性和效率有着直接的影响。若{w_2}过大,路径会过于保守,导致长度增加、任务时间延长,效率下降;而{w_1}过大则使路径规划偏向接近目标点,忽视障碍物,增加避障难度并降低成功率。合理调整{w_1}和{w_2}能在安全性和效率间找到平衡点,使无人艇在较短路径上有效避开障碍物,既保证任务安全性,又提升执行效率。因此,根据任务需求选择适当的权重值对优化路径规划至关重要。
4. 结 论
本文针对无人艇在仅依赖局部状态感知条件下如何高效完成海上搜救任务,提出了一种基于局部状态感知的深度强化学习无人艇路径规划方法。首先,本文以SAC算法为基础框架,设计了专门适用于局部感知场景的多目标奖励函数,解决了传统强化学习在不确定环境中鲁棒性不足的问题,使算法能够在高不确定环境中实现更优的路径规划策略。其次,针对SAC算法在大规模随机环境中训练效率低的问题,本文提出了FESAC算法。该算法通过提取环境关键特征并在随机特征环境中进行训练,显著提升了采样效率与模型收敛速度。最后,为解决局部感知与全局规划之间的矛盾,本文设计了基于局部感知域的迭代航路点规划方法。该方法通过迭代规划局部航路点,将大范围海上搜救任务分解为一系列与FESAC算法相匹配的短期避障子任务,构建了从局部到全局的路径规划完整解决方案。这种分解策略有效克服了局部感知的限制,实现了全局最优与局部可行的平衡。仿真结果证明本文提出的方法在海上搜救任务中具有出色的鲁棒性和高效性;通过合理设计参数,实现了任务安全性与效率的平衡。
本文提出的基于局部状态感知的深度强化学习无人艇路径规划方法在海上搜救任务中展现了良好的鲁棒性和有效性,但仍存在动态障碍物处理不足、环境建模简化等局限。未来研究可聚焦于动态障碍物避碰、真实海洋环境建模等方向,以进一步提升算法在实际复杂海况中的适应性和实用性,更好地满足真实搜救任务需求。
-
表 1 FESAC算法伪代码
Table 1 Pseudo-code of FESAC algorithm
算法1:FESAC算法 输入:网络参数\phi ,\psi ,\psi ',{\theta _1},{\theta _2} 1: 初始化网络参数\phi ,\psi ,\psi ',{\theta _1},{\theta _2},创建经验回放池\mathcal{D},建立特征增强随机特征环境 2: for 训练周期e = 1,2,...,E do: 3: 初始化环境状态{s_0},设置索引{d_0} = 0 4: for 时间步t = 1,2,...,T do: 5: 获取状态{s_t}并采样获得动作{a_t} \sim {\pi _\phi }( \cdot |{s_t}) 6: 获取奖励{r_t}、状态{s_{t + 1}}和索引{d_t} 7: 将({s_t},{a_t},{r_t},{s_{t + 1}},{d_t})存储到经验回放池\mathcal{D} 8: if t = T,开始训练网络: 9: for 训练轮次k = 1,2,...,K do: 10: 从\mathcal{D}中随机采样m组数据: 11: 更新网络参数: {\theta _1} \leftarrow {\theta _1} - \lambda {\nabla _{{\theta _1}}}{L_Q}({\theta _1}) {\theta _2} \leftarrow {\theta _2} - \lambda {\nabla _{{\theta _2}}}{L_Q}({\theta _2}) \psi \leftarrow \psi - \lambda {\nabla _\psi }{L_V}(\psi ) \psi ' \leftarrow \sigma \psi + (1 - \sigma )\psi ' \phi \leftarrow \phi - \lambda {\nabla _\phi }{L_\pi }(\phi ) \alpha \leftarrow \alpha - \lambda {\nabla _\alpha }L(\alpha ) 12: end for 13: else 14: 继续与环境交互 15: end if 16: end for 17: end for 表 2 FESAC超参数设置
Table 2 Hyperparameter configuration of FESAC algorithm
参数 值 折扣因子\gamma 0.99 学习率\lambda 0.001 批次大小 256 经验池容量 1 000 000 优化器 Adam 表 3 仿真参数
Table 3 Simulation parameters
参数类别 参数名称 值 运动学参数 {\tau _u} [−400 N, 400 N] {\tau _r} [−20 N, 20 N] 奖励函数参数 p 1.0 航路点规划参数 {r_{\text{e}}} 100 m {r_{\text{c}}} 75 m m 360 表 4 不同参数下路径规划结果
Table 4 Path planning results under different parameters
策略 {w_1} {w_2} 路径长度/m 成功率/% #1 0.8 1.2 1 721.3 93 #2 0.9 1.1 1 574.7 90 #3 1.0 1.0 1 534.6 80 #4 1.1 0.9 1 535.2 72 #5 1.2 0.8 1 576.4 65 -
[1] 李贺, 王宁, 薛皓原. 水面无人艇领航−跟随固定时间编队控制[J]. 中国舰船研究, 2020, 15(2): 111–118. doi: 10.19693/j.issn.1673-3185.01755 LI H, WANG N, XUE H Y. Leader-follower fixed-time formation control of unmanned surface vehicles[J]. Chinese Journal of Ship Research, 2020, 15(2): 111–118 (in Chinese). doi: 10.19693/j.issn.1673-3185.01755
[2] WANG N, LIU Y J, LIU J L, et al. Reinforcement learning swarm of self-organizing unmanned surface vehicles with unavailable dynamics[J]. Ocean Engineering, 2023, 289: 116313. doi: 10.1016/j.oceaneng.2023.116313
[3] NI S K, WANG N, QIN Z Y, et al. A distributed coordinated path planning algorithm for maritime autonomous surface ship[J]. Ocean Engineering, 2023, 271: 113759. doi: 10.1016/j.oceaneng.2023.113759
[4] 刘祥, 叶晓明, 王泉斌, 等. 无人水面艇局部路径规划算法研究综述[J]. 中国舰船研究, 2021, 16(S1): 1–10. doi: 10.19693/j.issn.1673-3185.02538 LIU X, YE X M, WANG Q B, et al. Review on the research of local path planning algorithms for unmanned surface vehicles[J]. Chinese Journal of Ship Research, 2021, 16(S1): 1–10 (in Chinese). doi: 10.19693/j.issn.1673-3185.02538
[5] WANG N, SONG J L, DONG Q. Structural design of a wave-adaptive unmanned quadramaran with independent suspension[J]. IEEE Transactions on Intelligent Transportation Systems, 2024, 25(9): 12395–12406. doi: 10.1109/TITS.2024.3375278
[6] 杨成斌, 吴晓阳, 张鲁君, 等. 智能无人艇关键技术需求分析研究[J]. 科技创新与应用, 2024, 14(28): 8–14. doi: 10.19981/j.CN23-1581/G3.2024.28.002 YANG C B, WU X Y, ZHANG L J, et al. The development of high-performance unmanned surface vehicles with strong artificial intelligence[J]. Technology Innovation and Application, 2024, 14(28): 8–14 (in Chinese). doi: 10.19981/j.CN23-1581/G3.2024.28.002
[7] 周治国, 余思雨, 于家宝, 等. 面向无人艇的T-DQN智能避障算法研究[J]. 自动化学报, 2023, 49(8): 1645–1655. doi: 10.16383/j.aas.c210080 ZHOU Z G, YU S Y, YU J B, et al. Research on T-DQN intelligent obstacle avoidance algorithm of unmanned surface vehicle[J]. Acta Automatica Sinica, 2023, 49(8): 1645–1655 (in Chinese). doi: 10.16383/j.aas.c210080
[8] WANG N, HE H K, HOU Y L, et al. Model-free visual servo swarming of manned-unmanned surface vehicles with visibility maintenance and collision avoidance[J]. IEEE Transactions on Intelligent Transportation Systems, 2024, 25(1): 697–709. doi: 10.1109/TITS.2023.3310430
[9] 胡智焕, 杨子恒, 张卫东. 基于混合A*搜索和贝塞尔曲线的船舶进港和靠泊路径规划算法[J]. 中国舰船研究, 2024, 19(1): 220–229. doi: 10.19693/j.issn.1673-3185.03232 HU Z H, YANG Z H, ZHANG W D. Path planning for auto docking of underactuated ships based on Bezier curve and hybrid A* search algorithm[J]. Chinese Journal of Ship Research, 2024, 19(1): 220–229 (in Chinese). doi: 10.19693/j.issn.1673-3185.03232
[10] MAHMOUDZADEH S, ABBASI A, YAZDANI A, et al. Uninterrupted path planning system for Multi-USV sampling mission in a cluttered ocean environment[J]. Ocean engineering, 2022, 254: 111328. doi: 10.1016/j.oceaneng.2022.111328
[11] RAHEEM F A, RAAFAT S M, MAHDI S M. Robot path-planning research applications in static and dynamic environments[M]//FURZE J N, ESLAMIAN S, RAAFAT S M, et al. Earth Systems Protection and Sustainability. Cham: Springer, 2022: 291−325. doi: 10.1007/978-3-030-85829-2_12.
[12] 张天浩, 池晴佳, 林永水, 等. 基于人工势场法改进MADDPG算法的AUV协同应召搜潜航路规划研究[J]. 中国舰船研究, 2025: 1−13. doi: 10.19693/j.issn.1673-3185.04229. ZHANG T H, CHI Q J, LIN Y S, et al. On-call antisubmarine path planning for AUVs based on an artificial potential field-enhanced MADDPG algorithm[J]. Chinese Journal of Ship Research, 2025: 1−13. doi: 10.19693/j.issn.1673-3185.04229 (in Chinese).
[13] LI P Y, HAO L J, ZHAO Y J, et al. Robot obstacle avoidance optimization by A* and DWA fusion algorithm[J]. PLoS One, 2024, 19(4): e0302026. doi: 10.1371/journal.pone.0302026
[14] ZHANG W L, SHAN L, CHANG L, et al. SVF-RRT*: A stream-based VF-RRT* for USVs path planning considering ocean currents[J]. IEEE Robotics and Automation Letters, 2023, 8(4): 2413–2420. doi: 10.1109/LRA.2023.3245409
[15] ZHAO L, BAI Y. Data harvesting in uncharted waters: Interactive learning empowered path planning for USV-assisted maritime data collection under fully unknown environments[J]. Ocean Engineering, 2023, 287(1): 115781. doi: 10.1016/j.oceaneng.2023.115781
[16] QU T C, XIONG G, ALI H, et al. USV path planning under marine environment simulation using DWA and safe reinforcement learning[C]//2023 IEEE 19th International Conference on Automation Science and Engineering (CASE). Auckland, New Zealand: IEEE, 2023: 1-6. doi: 10.1109/CASE56687.2023.10260584.
[17] GUAN W, ZHAO M Y, ZHANG C B, et al. Generalized behavior decision-making model for ship collision avoidance via reinforcement learning method[J]. Journal of Marine Science and Engineering, 2023, 11(2): 273. doi: 10.3390/jmse11020273
[18] WU C B, YU W N, LI G Z, et al. Deep reinforcement learning with dynamic window approach based collision avoidance path planning for maritime autonomous surface ships[J]. Ocean Engineering, 2023, 284: 115208. doi: 10.1016/j.oceaneng.2023.115208
[19] LIU Y Z, CHEN H, ZOU Q, et al. Automatic navigation of microswarms for dynamic obstacle avoidance[J]. IEEE Transactions on Robotics, 2023, 39(4): 2770–2785. doi: 10.1109/TRO.2023.3263773
[20] YANG X, HAN Q L. Improved reinforcement learning for collision-free local path planning of dynamic obstacle[J]. Ocean Engineering, 2023, 283: 115040. doi: 10.1016/j.oceaneng.2023.115040
[21] SUN Z Y, SUN H B, LI P, et al. Cooperative strategy for pursuit-evasion problem in the presence of static and dynamic obstacles[J]. Ocean Engineering, 2023, 279: 114476. doi: 10.1016/j.oceaneng.2023.114476
[22] WANG P, LIU R R, TIAN X L, et al. Obstacle avoidance for environmentally-driven USVs based on deep reinforcement learning in large-scale uncertain environments[J]. Ocean Engineering, 2023, 270: 113670. doi: 10.1016/j.oceaneng.2023.113670



 下载:
下载: