0.   引　言

复杂船舶舱段结构优化问题涵盖范围广、设计参数众多，一般采用有限元方法来获得舱段结构的各特征物理量，如应力、失稳特征值和变形等。通过有限元法计算的目标函数/约束条件难以获得其梯度信息，而传统的基于梯度的数学优化算法又难以应用。元启发式算法虽然不需要目标函数/约束条件的梯度信息，但需要对目标函数/约束条件进行大量的采样（即真实函数评估）。常琦^[1]使用Isight集成MSC.Patran/Nastran，并采用粒子群算法在HCSR规范约束下对47个设计变量的舱段结构进行了优化设计，结果显示可使整体重量下降0.28%。李振洋^[2]同样利用Isight直接集成MSC.Patran/Nastran，并采用自适应模拟退火算法对84个设计变量的船舶舱段结构进行了优化，结果显示结构减重了5.762%。Ma等^[3]和Kim等^[4]将舱段结构优化问题转化为了多个加筋板架优化问题，其首先利用舱段的有限元模型计算出各个板架所受到的边界位移载荷，然后基于这些边界条件，采用半解析解进行板架结构的优化，一旦得到所有板架结构的优化解，算法会更新舱段结构的有限元模型并再次对板架进行优化计算。上述优化方法是直接使用元启发式算法嵌套有限元计算，计算成本较高。

目前，国内外已有研究通过使用代理模型预测舱段结构的特征响应值来辅助优化算法进行优化，以降低算法的计算成本。袁野等^[5]以支持向量机为代理模型，使用遗传算法对有23个设计变量的多用途船货舱部分舱段进行优化，成功实现了舱段结构减重7.23%，并且优化结果与直接嵌套有限元的遗传算法结果十分接近，而计算量则仅为后者的1/4。汪俊泽等^[6]提出了一种基于子模型分解的代理模型协同优化方法，其通过将高维的舱段结构优化问题转化为多个板架结构优化问题，避免了直接构建高维代理模型所面临的困难，同时，还在板架结构优化子问题中使用板架结构代理模型替代舱段结构的有限元模型，降低了计算成本。此外，汪俊泽^[7]还提出了一种基于降维代理模型的舱段结构优化方法，即利用基于相关系数的降维技术来提高高维环境下代理模型的预测精度，结果显示与基于降维代理模型的优化方法相比，基于子模型分解的优化方法效果更好，实现了75个设计变量的舱段结构减重4.96%。

一方面，由于缺乏高效成熟的大规模优化算法，上述研究大多局限于中、低维度的舱段结构优化问题。当要进一步进行舱段结构精细化设计时，变刚度（即变腹板高、腹板厚等）桁材将是必然选择。若将不等刚度的变截面梁的每一段构件尺寸以及桁材布局参数（即桁材间距）都作为设计变量的话，舱段结构优化问题的设计变量的个数将迅速增加，可以高达几百个。另一方面，已有的研究多使用成熟的元启发式算法，即将船舶结构优化问题看成一个黑箱问题直接进行求解。这种做法虽然可以获得满意的结果，但计算成本较高。然而，若能融入船舶结构力学先验知识，有针对性地指导优化算法的设计，使船舶典型结构优化问题对于优化算法来说不再是完全的“黑箱”，将有效提升算法的寻优效率，进一步提高最终优化解的质量。通常，船舶结构优化问题有大量的先验知识可以利用，包括但不限于：1）单调性，增大构件尺寸会降低结构的应力、增加结构重量等；2）局部性，改变某个局部构件的尺寸，通常对该构件的应力改变较大，对其他构件的应力改变相对较小；3）耦合性，船舶结构优化往往涉及多个设计变量之间的耦合效应，通过先验知识，可以了解到某些设计变量之间耦合作用的强弱；4）敏度，通过先验知识设计变量对目标函数/约束条件的影响程度大小；5）历史数据，例如之前对类似结构进行过优化，这些优化历史数据可以帮助算法更好地理解设计空间的特点和可能的优化解位置等。若能有效利用这些知识，可以指导黑箱算法在设计空间中选择合适的搜索方向，加速收敛并避免无效搜索。

对优化算法来说，一旦设计变量的维度过高，一方面算法对于高维优化问题的寻优能力下降，另一方面，建立可靠代理模型的难度增加，代理模型本身的计算复杂度以及所需的样本点数急剧增加，优化结果难以保证。本文将舱段结构的所有纵向桁材（即甲板纵桁、舷侧纵桁和船底龙骨）和横向桁材（即甲板强横梁、舷侧强肋骨、船底实肋板）的位置参数（即布局型设计变量）以及变刚度截面尺寸参数（即尺寸型设计变量）作为设计变量，以舱段整体结构的重量为目标函数，各纵横向构件的弯曲正应力、剪应力、位移以及甲板板架的稳定性为约束条件，提出对应的优化数学模型以及有限元参数化模型，并针对构成的大规模舱段优化问题，基于文献[8]提出的双种群协同差分进化算法，融合代理模型以及力学先验知识，提出先验知识驱动的船舶舱段结构布局及尺寸优化算法。该算法利用构件应力和变形的单调性以及局部性，将设计变量分为桁材的布局和尺寸两类，将原问题分解为一系列低维子问题，优先处理约束裕度大的子问题，其中由布局变量所形成子问题的优化目标是最小化约束裕度，由各桁材尺寸变量所形成子问题的优化目标是舱段结构重量，然后使用代理模型快速预测各物理量，并仅考虑约束代理模型的加点准则。

1.   分解优化算法基本理论

一般而言，一个单目标约束实数优化问题可以采用下式表述：

式中：$f({\boldsymbol{x}})$为目标函数；${\boldsymbol{x}}$为d维的决策向量，也称为设计变量；$g_{i}({\boldsymbol{x}})$，$h_{j}({\boldsymbol{x}})$分别为第i个不等式约束和第j个等式约束。如果式（1）中的维度d足够大（在进化计算领域中通常意味着d远大于100），则称其为大规模单目标约束优化问题^[9-10]。如果目标函数和约束条件以及其梯度表达式不可知，则称其为大规模黑箱单目标约束优化问题。此外，若目标或约束的获得成本高昂，例如通过耗时的数值仿真或实验得到，则称其为昂贵大规模黑箱单目标约束优化问题。

分解优化框架是求解大规模优化问题的有效手段之一，其伪代码流程如算法1所示。

可以看到，分解优化框架是通过将原始的大规模优化问题分解为一系列低维的子问题来分别进行求解，每个子问题的设计变量仅为原始问题的一部分（子集）。在优化某个子问题时，需要与其他子问题的最优解（或代表解）协作，拼凑成一个完整的解以评价其目标函数值和约束函数值。这一过程反复迭代，每个子问题的最优解更新取决于其余子问题所提供的最优解（或代表解），并且其本身的最优解（或代表解）更新也会影响其余子问题的最优解位置，从而实现子问题之间的“协同”优化。值得注意的是，若不同子问题的设计变量之间存在耦合效应，分解优化框架并不能保证获得的最优解一定为原问题的全局最优解。

2.   船舶舱段结构有限元分析及优化数学模型

2.1   有限元参数化模型与分析

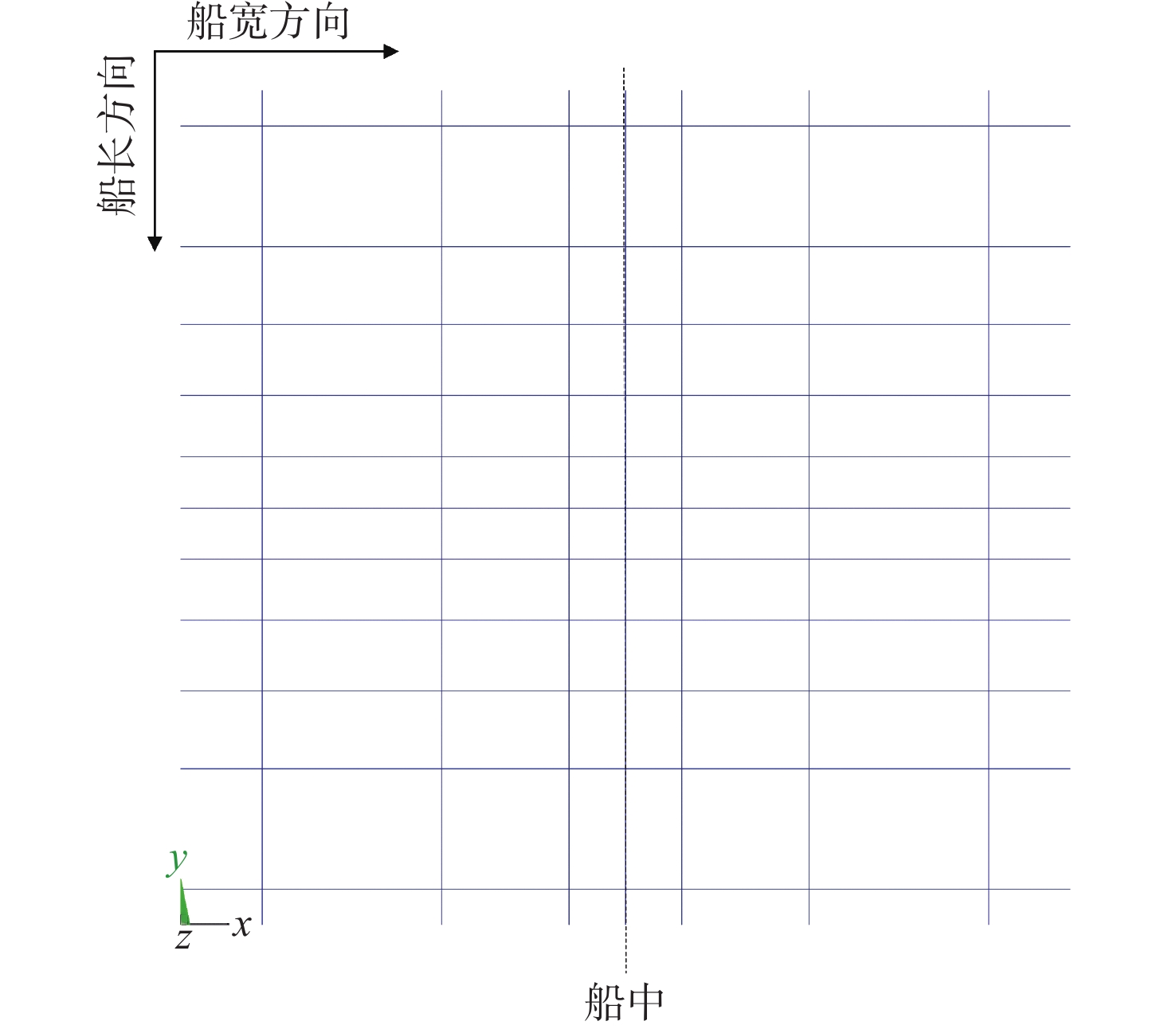
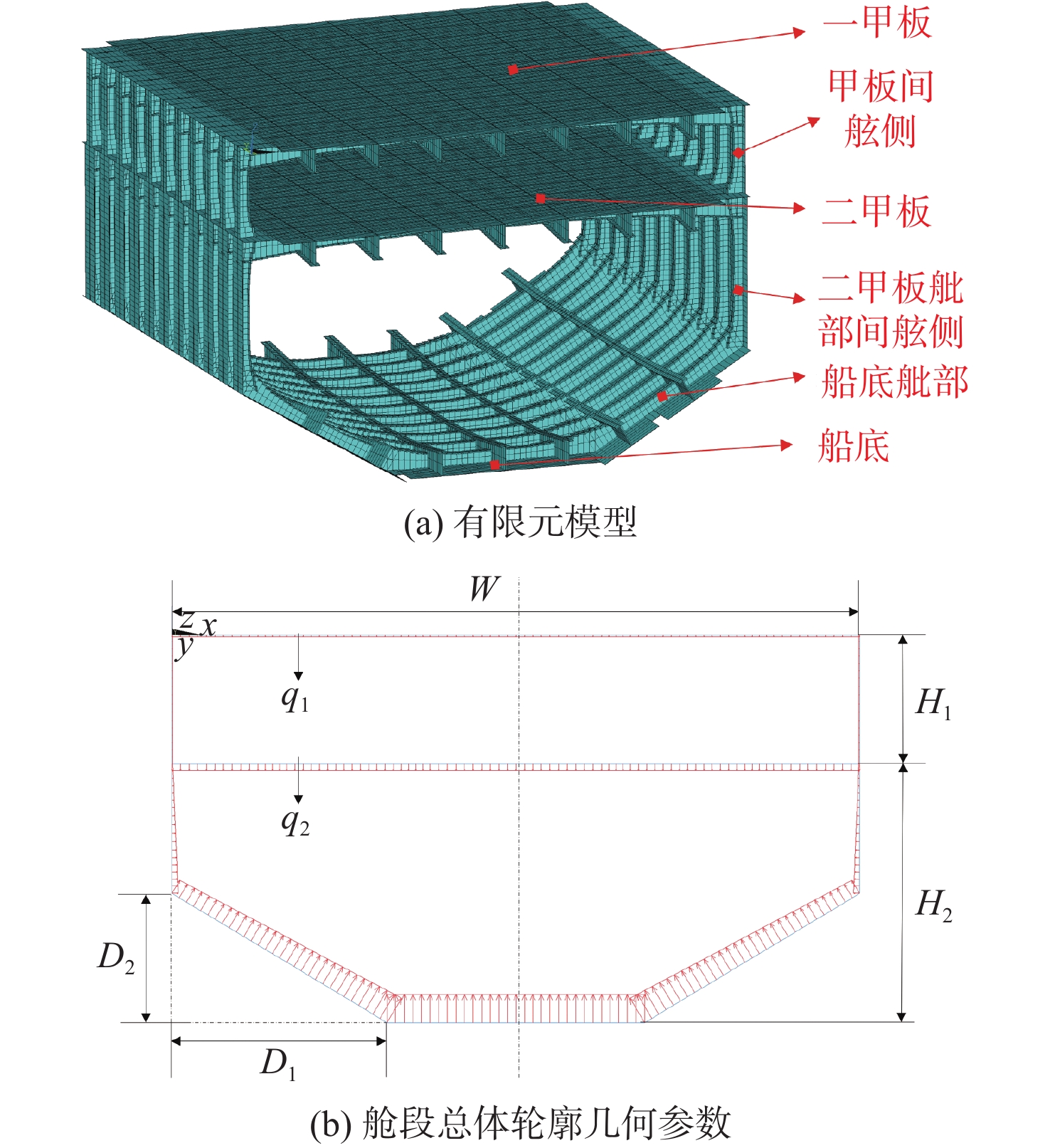
本文研究的舱段包含2层甲板板架、舷侧板架以及船底（包括舭部）板架。上甲板包含7根纵向构件和11根横向构件。每层甲板以及船底（包括舭部）的纵向构件和横向构件布局相同。将每个板架简化为交叉梁系，纵骨以等效面积的形式均摊于纵向构件附连带板的厚度上。纵向构件和横向构件使用工字钢截面的Beam 188梁单元模拟。其ANSYS有限元模型示意图以及舱段整体的几何参数如图1所示。

图  1  舱段结构有限元模型以及几何参数示意图

Figure  1.  Finite element model of cabin structure and its geometric parameters

下载: 全尺寸图片 幻灯片

图1中，红色箭头代表载荷（${q_1}$，${q_2}$分别为一层甲板和二层甲板的均布载荷大小），其具体的施加方式将在后文中说明。设第1层甲板的坐标原点为z，x轴方向指向船宽，y轴方向指向船长，则确定舱段整体几何形式的参变量包括：第1，2层甲板的层高$H_{1}$和$H_{2}$、舭部位置几何参数$D_{1}$和$D_{2}$，以及船宽$W$和舱段长度$L$。上述几何参数可唯一确定该舱段的总体轮廓位置分布，本节提出的舱段几何参数模型可以很容易地扩展至更多层甲板的情形。

确定了舱段整体总体几何参数后，第i根甲板纵桁（横梁）的位置可以分别由其距离y（x）轴的距离$d_{i}^{l}$（$d_{i}^{t}$）唯一确定。需要指出的是，对于船底（包括舭部）而言，一个横向构件的位置变量可同时定位3根横向构件（左侧舭部、船底、右侧舭部）。在确定了甲板及船底横向构件的位置后，舷侧肋骨的位置也随之唯一确定，如图1所示。每一层甲板和船底（包括舭部）都具有相同的纵向构件以及横向构件布局，但每一层甲板和船底（包括舭部）以及舷侧的各个构件的尺寸变量可以不同。

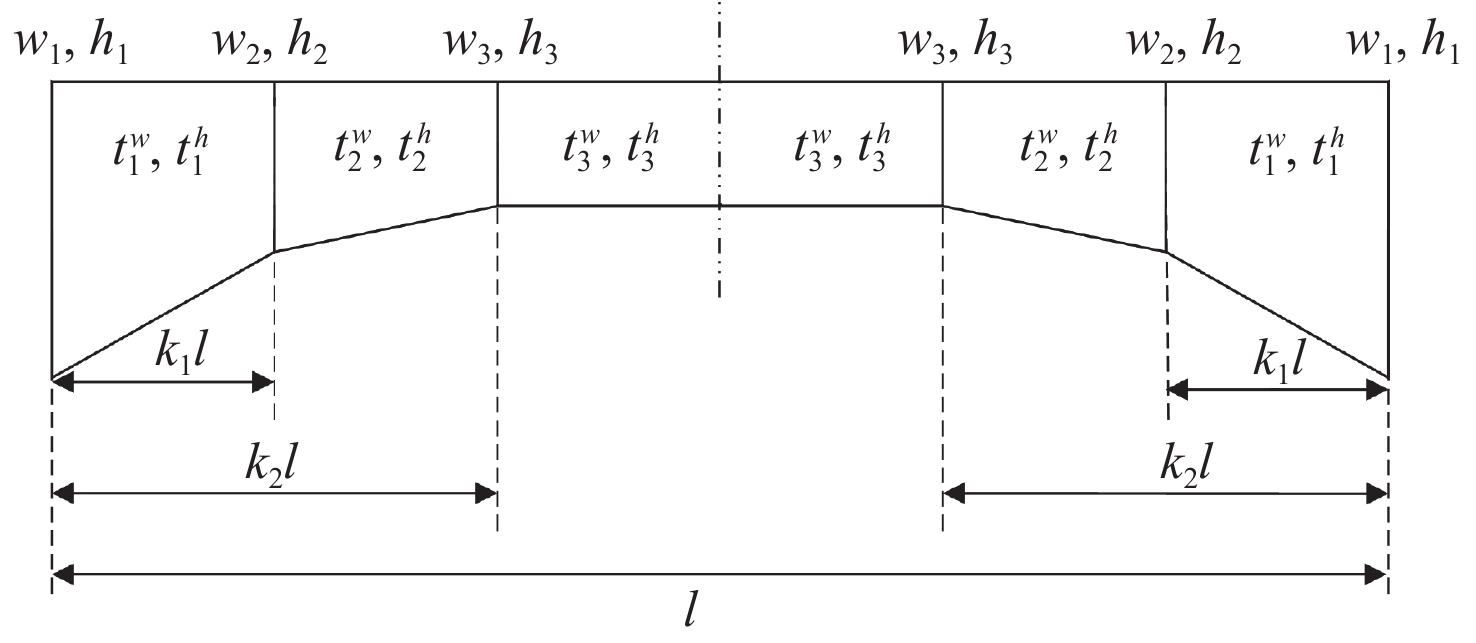
本文将纵向构件和横向构件均视为如图2所示的变截面梁。

图  2  梁尺寸变量示意图

Figure  2.  Beam dimension variables

下载: 全尺寸图片 幻灯片

图2所示为一对称的变截面梁的尺寸变量示意图。本文将纵向/横向构件梁视为T型材截面，设梁的总长度为$l$，则在梁端点和距离端点$k_{1} l$，$k_{2} l$处分别设置不同的梁截面1，2，3，本文分别设$k_{1}=1 / 6$，$k_{2}=1 / 3$。$w_{i}$和$h_{i}$分别为第i个梁截面的面板宽和腹板高，两个梁截面之间的截面面板宽和腹板高线性变化。两个梁截面之间的截面面板厚$t_i^{w}$和腹板厚$t_{i}^{h}$为常数，沿梁的方向呈阶跃变化。由于每根梁的长度在优化过程中是固定的参变量，故每根梁一共有12个尺寸变量。

铺板和纵骨的作用以横向构件及纵向构件附连带板的形式考虑。在给定纵向构件和横向构件的布局位置变量后，附连带板的厚度以及宽度按如下流程自动确定。

首先，根据式（2）确定相邻两个纵向构件之间的纵骨间距与纵骨数量：

式中：$\left\| {d_i^{\rm{long}} - d_j^{\rm{long}}} \right\|$为相邻两根纵向构件i，j之间的间距；$nu{m_{\rm{long}}}$和$dis{t_{\rm{long}}}$分别为最终确定的这2个纵向构件之间的纵骨数量与间距；${d_{\max }}$为人为事先给定的最大纵骨间距。

然后，由满足局部强度要求的最小厚度确定每个板架的铺板厚度，按下式计算：

式中：${t_{\rm{panel}}}$为铺板厚度；b为该板架相邻两个纵向构件间的纵骨间距；$\sigma _{\rm{s}}^{\rm{panel}}$为板的许用应力；k为系数，取k = 0.5；$q$为作用于铺板上的载荷（出于安全考虑，计算舷侧结构板厚时，取载荷最大处的载荷值进行计算）。最终的铺板厚度由满足式（3）的最小厚度和人为给定的最小板厚$t_{\min }$取较大值得到。

纵骨尺寸从型材库中选择同时满足如下局部强度要求和稳定性要求的最轻尺寸的型材。

式中：$q$为压强载荷大小；a和b分别为纵骨跨距和间距；W为包括附连带板的纵骨的剖面模数；E为弹性模量；i为包括附连带板的纵骨的剖面惯性矩；f为不包括附连带板的纵骨剖面积；${b_{\rm{e}}}$和${t_{\rm{panel}}}$分别为纵骨的附连带板的宽度和厚度；$\sigma _{\rm{s}}^{\rm{long}}$和${\sigma _{\rm{s}}}$分别为纵骨的许用应力与材料屈服极限；${k_{\rm{s}}}$为系数，本文取${k_{\rm{s}}} = 2$。

最终，纵向构件的附连带板的宽度通过在纵向构件两侧间距的均值和纵向构件跨距1/6中取较小者确定，厚度取铺板厚度加上将纵骨面积均摊至铺板的等效厚度确定。横向构件的附连带板的宽度通过在横向构件两侧间距的均值和横向构件跨距1/6中取较小者确定，厚度取铺板厚度。考虑了附连带板后的梁截面在ANSYS软件中最终以工字钢截面的Beam 188单元模拟。

进行静强度计算时，舱段的边界条件为舱段两端所有节点刚性固定，对于1，2层甲板，其载荷为作用于横向构件上的均布线载荷。取构件梁单元腹板上、下端点处的最大弯曲正应力作为该构件的最大弯曲正应力。在对1甲板进行稳定性计算时，获得1甲板失稳欧拉应力$\sigma_{\mathrm{E}}$的步骤如下：

1）删除除1甲板以外的所有几何、有限元模型以及载荷。

2）对1甲板的3个边简支。固定第4边船宽和型深方向的平动自由度，沿船长方向施加单位位移载荷，进行屈曲分析；取第1阶失稳时位移最大的纵向构件的一段（一根纵向构件可以被横向构件分成多段）作为失稳构件，取静力结果中失稳构件结构的最小正应力值（绝对值最大）乘以第1阶失稳特征值即可得到失稳欧拉应力$\sigma_{\mathrm{E}}$。

2.2   优化数学模型

船舶舱段布局与尺寸优化的目标函数为最小化结构重量（体积）。设计变量为纵向构件和横向构件的布局位置参数$d_{i}^{l}$，$d_{i}^{t}$以及其尺寸参数。约束条件为纵向构件/横向构件的最大弯曲正应力、剪应力和位移，1甲板的失稳欧拉应力以及桁材的布置位置约束如式（6）所示。

式中：$x$为设计向量；$f(x)$为目标函数（整个舱段纵/横向构件的体积之和）；$V_{i}$为第i根构件的体积；k为整个舱段纵/横向构件的数量。$\sigma_{i}$，$\tau_{i}$，$\delta_{i}$分别为整个舱段第i根纵/横向构件的最大弯曲正应力、剪应力和挠度；${\delta _{\rm{s}}}$为构件允许发生的最大位移，本文取船宽的1/500；$d_{\min } \geq \hat{d}_{\min }$代表同向构件之间的最小距离$d_{\text {min}}$不得小于许用的最小距离$\hat{d}_{\text {min }}$。

3.   先验知识驱动的舱段结构优化算法

3.1   优化算法整体框架

本节基于舱段结构的力学特性，提出了先验知识驱动的舱段结构布局与尺寸分解优化算法，其整体流程伪代码如算法2下所示。

可以看到，算法2使用分解方法作为基本的优化框架，基于船舶结构力学先验知识，对通用黑箱优化算法做出了改进。算法2第6步中，优化每个子问题时，使用文献^[8]中提出的双种群协同差分进化（BiP-CDE）算法作为子问题的优化求解器。由于舱段结构各特征量是由有限元计算得到，是个耗时的过程，因此，在算法2第6步中使用代理模型辅助BiP-CDE算法进行优化，即在对子问题进行优化前，先生成样本点采样，对目标函数和约束条件使用高斯过程回归模型进行拟合，在评价个体适应度值时，使用高斯过程回归模型对个体的目标和约束进行预测，然后从中选择个体进行真实的函数评估作为新增样本点，并更新代理模型。

3.2   基于先验知识的分组方案

本文所研究舱段立体结构的载荷以及边界条件沿船长和船宽方向具有对称性，因此，优化解对应的舱段结构在空间上也是对称的。基于对称性，可以实现设计空间的特征选择，即仅需确定船宽及船长方向一半的桁材的布局位置变量和尺寸变量，剩余桁材的布局位置变量和尺寸变量通过镜像对称的方式补充完整即可。因此，基于对称性的特征选择可使设计变量的维数约降低至原始问题的1/4～1/3。

其次，各桁材的分布位置从理论上讲不会过于集中，因此，可以将各桁材布局位置变量的上下界进行空间缩减，即先沿船长/船宽方向，根据横向构件/纵向构件的根数将其均匀分段，每根桁材的位置只允许其落在对应的分段内，而非整个船长/船宽的长度。因此，基于先验知识的空间缩减可以大幅降低设计空间的体积。

本文基于先验知识进行分组，分组方案如下：

1）所有桁材的布局位置变量单独分为一组；

2）每根桁材的尺寸变量各自分为一组。

该分组方案基于如下先验知识：

首先，目标函数为舱段的重量（体积），可以由每根桁材的重量（体积）累加得到，因此，由每根桁材的尺寸变量形成的子问题一定是互相加法可分的。

其次，约束条件中绝大多数的特征量（正应力、剪应力和位移）仅与桁材本身的尺寸变量强相关，受其他桁材变量的影响较弱，每根桁材自身的尺寸变量耦合程度较高，与其他桁材的尺寸变量耦合程度较低。因此，将每根桁材自身的尺寸变量作为一个子问题是一个合理的选择。

此外，本文将桁材的位置变量与尺寸变量分开处理，所有的布局位置变量分到一个子问题内单独予以处理。这是因为本文假设每层甲板以及船底（包括舭部）的纵向/横向构件布局相同，因此，相比尺寸变量，位置变量的个数要少得多。其次，位置变量与尺寸变量的物理意义也不尽相同。因此，本文提出的算法也可以看作是位置布局优化与尺寸优化所形成的协同优化算法，即先固定布局变量优化尺寸变量，然后固定尺寸变量优化布局变量，反复迭代。值得指出的是，将位置变量与尺寸变量分开处理还可以带来另外一个好处，即由于有限元软件ANSYS的特性，当固定布局变量仅优化尺寸变量时，可以避免有限元软件重新划分网格，只需修改梁单元截面参数即可，这可大幅降低有限元软件的计算时间。由于舱段优化问题中占绝大多数的变量为尺寸变量，因此，固定位置变量仅优化尺寸变量可以大幅加快优化速度。同理，优化非1甲板尺寸及布局变量子问题时，可以不进行1甲板稳定性计算，再次加快有限元仿真计算速度。

3.3   基于先验知识的资源分配与目标函数选择策略

算法2第5步中将基于先验知识，根据当前最优解的状态，自动选择合适的子问题进行优化（资源分配策略），如算法3所示。

可以看到，算法3要求初始解为一可行解，该要求可以通过将所有设计变量取上界并适当调整纵横构件的位置来实现。算法3将首先优化未优化过的尺寸变量子问题，若所有的尺寸变量子问题已优化过，则优化布局位置变量子问题，实现布局与尺寸之间的协同优化，称为一轮优化。在选择未优化过的尺寸变量子问题时，优先选择约束裕度最大的构件对应的尺寸变量子问题。第i根构件的约束裕度$R_{i}$如下式所示：

可以看到，式（7）是先将构件的正应力、剪应力和位移进行归一化处理，然后从中选择最接近约束边界的物理量的裕度作为该构件的约束裕度，最终，选择约束裕度最大的构件进行优化。该做法是基于尺寸变量的单调性和局部性，即在优化某根构件的尺寸变量时，使目标函数下降的同时通常还会对约束条件造成不利影响，且仅对自身约束特征量的影响较大，对其他特征量的影响较小。因此，选择自身约束特征量裕度较大的构件进行优化，可以使目标函数下降的空间较大。

此外，在优化尺寸变量子问题时，其目标函数和约束条件与式（6）中相同，目标函数为舱段的重量（体积）。然而，在优化布局变量子问题时，其目标函数改为

式（8）中的负号表示极大化，即对于布局变量子问题，其目标为最小的约束裕度极大化。这是因为构件的位置几乎不会对结构重量造成影响，因此，布局变量优化的目标应该是调整各构件的位置，增大其最小约束裕度，为后续尺寸变量的优化创造更多的调整空间，从而实现布局与尺寸的协同优化。

3.4   基于先验知识的BiP-CDE子问题优化器

本文使用超参数迁移高斯过程回归模型辅助的双种群增强的协同差分进化（BiP-CDE）算法作为尺寸变量子问题优化器，其算法伪代码如下所示。

可以看到，该算法流程与文献[8]中的相同，故此处不再赘述算法细节。与文献[8]区别在于，种群个体的适应度值由高斯过程回归模型进行预测。并且，子问题的每代是选择种群中约束置信下边界（consLCB）最小的个体作为更新样本点。这是因为尺寸优化子问题的目标函数为重量（体积），可以由解析式获得，无需建立代理模型也没有误差，所以优化过程中仅需考虑提升约束边界附近的精度，随后使用文献^[11]提出的consLCB准则即可实现此目的。该准则可以逐步提高代理模型在约束边界附近的精度。

此外，值得注意的是，采用先验知识分组策略后，对于尺寸变量子问题，算法会先取该子问题设计变量的下限值进行计算，如果下限值是可行解，则直接以下限值作为该尺寸变量子问题的优化解返回；若下限值是不可行解，则将其作为样本点添加到初始样本点集中。该做法主要是基于单调性的先验知识，即目标函数一定是随着构件尺寸变量单调下降的，因此，如果下限值是可行解，则一定是该子问题的最优解，无需继续优化。

在优化布局位置变量子问题时，由于其目标函数值需要通过有限元计算获得，因此需要对目标函数建立代理模型，并且子问题的每代选择种群中置信下边界（LCB）值^[12]最小的个体作为更新样本点。

4.   优化结果及对比分析

4.1   算例参数设置

将提出的由先验知识驱动的BiP-CDE算法用于求解某舱段结构，以验证所提算法的有效性。求解时算法参数如下：分组策略为先验知识分组，合作者为当前最优解，子问题资源分配策略为按3.3节描述的按约束裕度的优化顺序，子问题代理模型辅助进化算法初始样本点大小为d(d+1)（d为子问题维数），停机准则为总函数评估次数达104，初始最优解为各构件位置均匀分布并且尺寸变量取上限。子问题优化器的参数设置如下：子问题种群大小为$\min \left(8 *\left(d_{\text {sub }}+2\right), 200\right)$，差分变异缩放因子$F=0.5$，差分进化交叉概率$C R=0.7$，多样性系数$K_{div}=0.1$，子问题停机准则为迭代添加的样本点个数达到阈值d。值得注意的是，在求解子问题时，每隔10代才会从种群中选择个体作为代理模型的样本点，而不是每一代都选择。这主要是因为对舱段结构进行有限元分析比较耗时，若每一代都从种群中选择个体添加样本点，计算成本将难以承受。

本文所求解立体舱段的材料为某船用高强钢，参数如下：屈服极限为390 MPa，弹性模量为2.1×10⁵ MPa，泊松比为0.3，密度为7 850 kg/m³。有限元网格大小为200 mm。整体几何参数如下：层高$H_{1}$= 3 000 mm，层高$H_{2}$= 6 000 mm，舭部位置参数$D_{1}$= 5 000 mm，舭部位置参数$D_{2}$= 3 000 mm，船宽$W$ = 16 000 mm，舱段长$L$ = 15 000 mm。载荷参数如下：1甲板载荷$q_{1}$= 5×10⁻³ MPa，2甲板载荷$q_{2}$= 1.5×10⁻² MPa，水线面处载荷$\hat{q}_{1}$= 5×10⁻³ MPa，水线面距1甲板距离h= 3 000 mm。各纵、横向构件梁截面尺寸变量的上、下界如表1所示。表中数值为T型材的取值，指“⊥腹板厚×腹板高/面板厚×面板宽”。

表  1  各纵横构件梁截面尺寸变量上下界

Table  1.  Up and low bounds of beam cross-section size variables for each longitudinal and transverse component

尺寸变量所属构件	下界	上界
1，2甲板纵、横向构件	⊥12×400/14×140	⊥16×460/18×180
舷侧构件	⊥12×400/14×140	⊥16×460/18×180
船底纵向构件	⊥12×400/14×140	⊥20×600/22×400
船底横向构件	⊥12×400/14×140	⊥20×600/22×300

下载: 导出CSV 

| 显示表格

4.2   优化结果及分析

优化结果如表2及图3所示。其中，最大弯曲应力、最大剪应力、最大位移和1甲板失稳欧拉应力的约束边界分别为234 MPa，117 MPa，32 mm和780 MPa。

表  2  先验知识驱动的代理模型辅助协同差分进化算法优化结果

Table  2.  Domain knowledge-driven surrogate-assisted model cooperative differential evolution algorithm optimization results

设计方案	特征物理量
	重量/t	最大弯曲 应力/MPa	最大剪 应力/MPa	最大 位移/mm	1甲板失稳欧拉 应力/MPa
初始解	92.72	193.13	48.75	17.09	1 085.20
优化解	52.35	234	69.29	24.06	780

下载: 导出CSV 

| 显示表格

图  3  甲板以及船底纵、和横向构件的布局位置优化结果（俯视图）

Figure  3.  Optimized layout positions of longitudinal and transverse components on the deck and ship bottom (top view)

下载: 全尺寸图片 幻灯片

可以看到，优化解重量为52.35 t，相比初始解（上界值，92.72 t）其重量降低了43.5%，相比下界值（51.30 t）重量仅提升了2%。最终所得的优化解构件最大弯曲应力（234 MPa）和1甲板失稳欧拉应力（780 MPa）达到了约束边界，优化非常充分。最大剪应力（69.2 9 MPa）和最大位移（24.06 mm）相较于约束边界仍有较大富余。从优化解的纵、横向构件的布局位置来看，纵、横向构件的分布呈现相同的特性，即靠近舱段中部的分布较为密集，距中部较远处的分布较为稀疏。

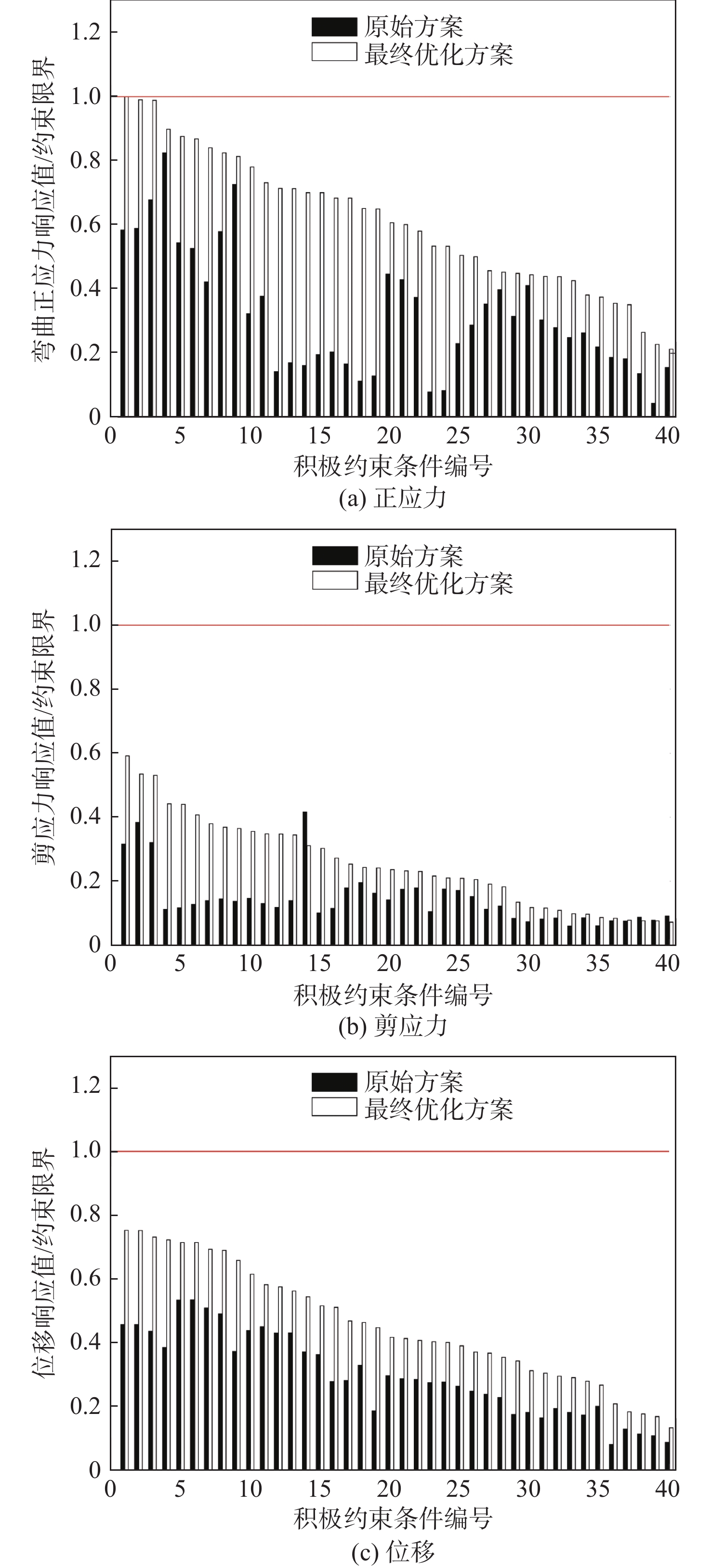
图4给出了最终优化解中约束裕度最少的前40个纵、横向构件的弯曲正应力、剪应力和位移的约束裕度优化前后对比。

图  4  各纵、横构件约束特征量裕度对比

Figure  4.  Comparison of constraint margin characteristics for longitudinal and transverse component

下载: 全尺寸图片 幻灯片

总的来看，绝大多数纵、横向构件的弯曲正应力、剪应力和位移的约束裕度在优化后均得以减小。其中，各纵、横向构件的弯曲正应力剩余的约束裕度最少，并且部分构件（主要是船底构件）的弯曲正应力落在约束边界附近；各纵、横向构件的位移约束裕度次之；各纵、横向构件的剪应力约束裕度最大。因此，综合来看，对于本文的立体舱段算例，控制重量的主要因素是船底（包括舭部）的强度要求以及1甲板的稳定性要求。

4.3   与无先验知识算法结果的对比

为进一步验证先验知识对优化算法的影响以及分解策略与代理模型的优势，本节将其与无先验知识的代理模型辅助协同差分进化算法以及使用差分进化算法直接嵌套有限元软件的方法进行了对比。由于基于对称性和均匀性的设计变量特征提取和空间缩减的先验知识较为常见且较为通用，故可以比较容易地应用于其他算法中。因此，为公平起见，本节进行对比的无先验知识的代理模型辅助协同差分进化算法以及使用差分进化算法直接嵌套有限元软件的方法均使用了基于先验知识的设计变量特征提取和空间缩减策略，对比的算法约束处理方式均为可行性准则。

差分进化算法直接嵌套有限元软件的方法使用普通差分进化算法将舱段优化问题视为一个整体，不进行分解直接求解；在计算个体适应度时直接调用有限元软件计算，不使用代理模型。其算法参数设置为：种群大小100，差分变异缩放因子$F=0.5$，差分进化交叉概率$C R=0.7$，子问题算法停机准则为进化代数达到100。

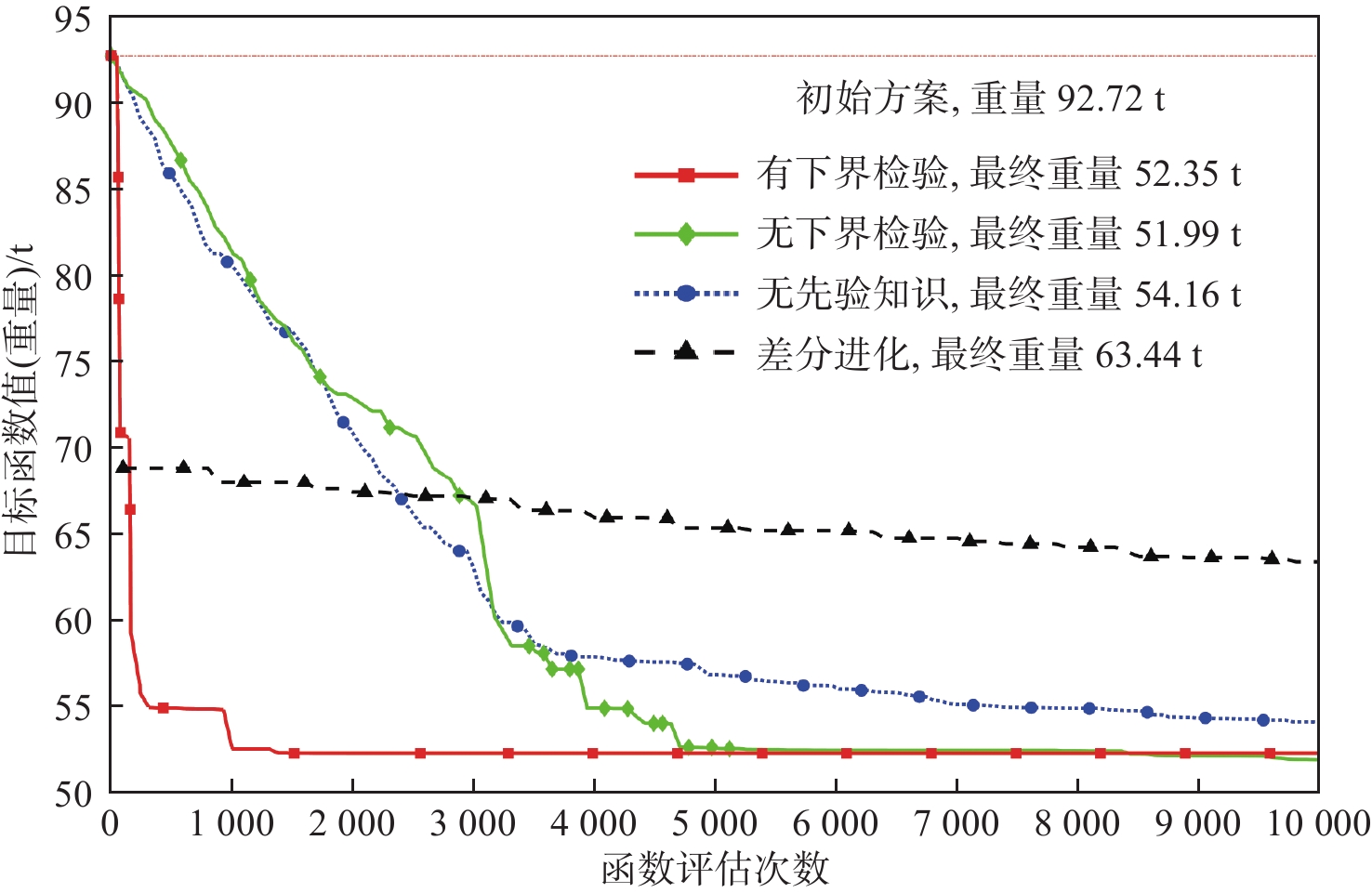
无先验知识的优化算法仍然使用与4.2节中相同的分解优化框架，但不使用基于先验知识的分组方案、资源分配与目标函数选择策略以及改进的BiP-CDE子问题优化器，其分组策略选择子问题大小为10的随机分组策略。其余算法参数的设置与4.1节中相同。此外，为进一步研究算法特性以及先验知识的多少对算法性能的影响，对于有先验知识辅助的算法，同时测试了有下界检测机制的算法以及无下界检测机制（即没有3.4节中所描述的下界检测机制）的算法。表3给出了各算法的最终优化结果对比，各个算法的收敛曲线对比如图5所示。

表  3  不同算法优化结果对比

Table  3.  Comparison of optimization results from different algorithms

设计方案	特征物理量
	重量/t	最大弯曲 应力/MPa	最大 剪应力/MPa	最大 位移/mm	1甲板失稳 欧拉应力/MPa
初始解	92.72	193.13	48.75	17.09	1 085.20
优化解	52.35	234	69.29	24.06	780

下载: 导出CSV 

| 显示表格

图  5  不同算法优化收敛曲线

Figure  5.  Convergence curves of different algorithms for optimization

下载: 全尺寸图片 幻灯片

从最终优化结果上可以看到，对于直接嵌套有限元的差分进化算法来说，其所得的优化解质量远差于使用了分解优化框架的2个算法；所得优化解的重量为63.44 t，并且其所有约束都未到达约束边界；即使使用了基于先验知识的特征选择和空间缩减技术，本文舱段算例的设计变量数目仍然高达580多个，没有分解框架以及代理模型的辅助，差分进化算法收敛速度极其缓慢，计算资源消耗巨大。

对于使用了分解优化框架的代理模型辅助协同差分进化算法的3个算法来说，采用这3个算法所得的最终优化解相近，使用了先验知识的2个算法优化解重量更低。采用3个算法所得的优化解的约束均达到约束边界，即弯曲应力与1甲板失稳欧拉应力达到边界，再次说明控制本文算例的约束主要是船底强度约束以及1甲板稳定性约束。

从收敛曲线上看，由于3个基于分解框架的算法以尺寸变量上界值为初始点，并且每次只优化部分变量，因此，在算法开始运行时，这3个算法的优化解要远差于差分进化算法。随着优化的进行，这3个基于分解框架的算法的收敛速度显著快于差分进化算法。其中，有下界检测机制的优化算法在算法开始后迅速收敛，仅花费1 500次左右的有限元仿真次数就获得了比无先验知识算法花费10 000次有限元仿真的最终优化解质量更好的解。无下界检测机制的优化算法虽然前期的收敛速度与无先验知识的算法相同，但后期所得优化解的质量是3个算法中最好的。其原因可能是算例中有部分构件的约束裕度充足（例如，舷侧构件和2甲板构件），这些构件可能尺寸变量取下界值仍然是可行解。因此，下界检测机制会直接返回当前下界值作为该构件子问题的最优解，有下界检测机制的优化算法前期收敛速度将非常快。然而，这种直接“优化到底”的算法，可能会因为变量间的耦合作用而导致后续其他构件无法再继续进行优化。例如，假设优化船底桁材A的尺寸时，算法会将船底桁材A的正应力值调整至许用应力边界附近；当采用算法优化舷侧桁材B的尺寸时，由于减小舷侧桁材B的尺寸可能会轻微增大船底桁材A的正应力（即使增大得可能不明显），致使船底桁材A的正应力不满足约束要求，从而导致无法继续优化舷侧桁材B的尺寸（即使此时舷侧桁材B本身的正应力约束裕度仍然较大）。而无下界检测机制的优化算法虽然前期没有快速收敛，但却给后续构件的优化留下了空间，因此取得了最好的优化解质量。这3个算法的对比充分说明本文融入的力学先验知识对算法性能的提升效果显著。

5.   结　语

本文针对船舶舱段结构布局以及尺寸优化这一具体的工程优化问题，基于船舶结构力学先验知识，将通用黑箱优化算法进行改进，提出了先验知识驱动的代理模型辅助协同差分进化的船舶舱段结构优化算法。先验知识分组策略考虑到舱段约束特征物理量大部分具有单调性和局部性的特点，以及目标函数单调性和加法可分性，将属于同一构件的尺寸变量分为一组，并将布局位置变量单独分为一组，实现了布局与尺寸间的协同优化。此外，还提出了基于约束裕度的子问题资源分配策略。在优化不同子问题时，根据子问题的单调性对子问题优化器进行了改进，并根据子问题设计变量的类型提出了目标函数切换策略。

通过将提出的算法应用于具体的舱段结构优化算例中，使得舱段的整体重量相较于上界值降低了43.5%，并且使船底纵向构件弯曲应力以及1甲板失稳欧拉应力接近于其约束限界值，使材料得到了充分、合理的利用。算法对比结果表明，相较于传统的不使用分解策略的差分进化算法，分解优化框架以及代理模型大幅提高了算法的寻优性能。基于先验知识提出的算法改进策略进一步大幅提升了代理模型辅助协同差分进化算法的性能，算法效率很高，体现了专业先验知识对于通用黑箱优化算法性能的改进。