0.   引　言

为应对船员短缺、降低人力成本、提升运营效率，研究无人、可靠、绿色的智能船舶迫在眉睫。作为智能航行中的关键技术之一，自主靠泊是其中相对复杂、困难的船舶控制问题，也是实现智能船舶无人化必不可少的一环^[1]。

在现有研究中，大型船舶的自主靠泊策略主要分为以下3种：泊位外镇定靠泊、直接平行靠泊以及先泊位外镇定再平行靠泊^[2]。泊位外镇定靠泊策略将船在泊位外1.5倍船长处镇定视为完成任务，不利于后续自动系泊操作，难以实现智能船舶的全过程无人化；直接平行靠泊则是借助舵和侧推器让船舶平行向泊位靠拢，由于没有考虑纵向运动，与自主靠泊实际操作不符；泊位外镇定再平行靠泊是指在泊位外的过渡点控制余速、调整船艏至与泊位平行后再向泊位靠拢，对于实现大型智能船舶全过程自主靠泊具有一定可行性。

船舶在港湾进行靠泊操作时，不仅需要抵御风、浪、流干扰，还应注意岸壁效应带来的“岸推”、“岸吸”影响^[3]。同时，低速域的靠泊运动、推进系统的物理限制，会引起控制模型不确定以及控制分配误差问题^[4]。针对上述多源干扰的处理，基于扰动观测器的控制（disturbance observer-based control，DOBC）和自抗扰控制（active disturbance rejection control，ADRC）均效果良好。Zhang等^[5]设计了扰动观测器，在线估计了由风、浪、流以及模型不确定带来的干扰。Yu等^[6]设计了一种神经网络ESO（neural network ESO，NNESO）用以解决动力定位船舶推进系统容错控制问题。吴文涛等^[7]针对模型不确定性和未知环境扰动设计了一种基于ESO的双桨推进目标跟踪算法。尽管ADRC技术在处理风、浪、流干扰的有效性已得到了广泛的验证，但鲜有人探讨其估计船舶靠泊过程中岸壁效应干扰的效果。

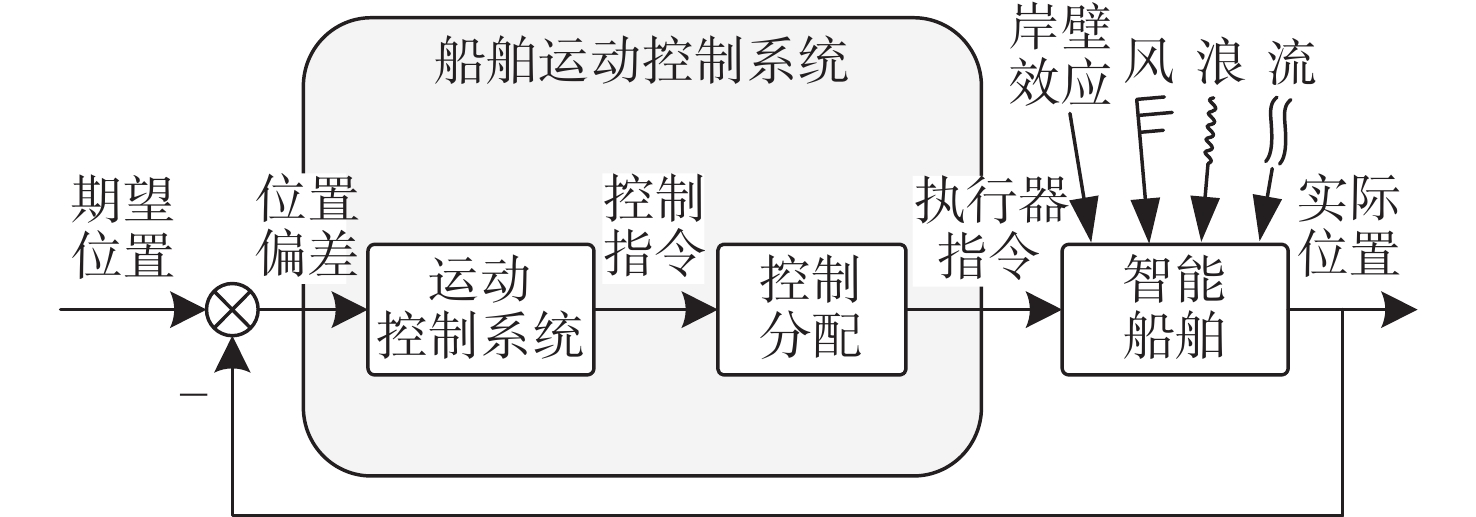
为实现自主靠泊，同时提高船舶运动控制的可靠性，智能船舶通常会装备由主推、舵、侧推器以及全回转等执行器组成的过驱动推进系统，故需要借由控制分配模块将上层控制器下发的三自由度控制指令准确、迅速并且合理地分配给各个执行器^[8]，如图1所示。

图  1  智能船舶控制系统框图

Figure  1.  Control system of the intelligent ship

下载: 全尺寸图片 幻灯片

广义逆法^[9]最早被用来求解此类控制分配问题，尽管后来出现了加权伪逆法^[10]、级联伪逆法^[11]等，但此类解析方法不能很好地处理执行器的物理约束，有可能造成较大的控制分配误差。此外，学者们还尝试将控制分配问题转化为二次规划（QP）问题后，使用有效集法^[12]、序列二次规划法^[13]等迭代方法进行求解，虽然提高了精确性，但在实时性方面有所牺牲。Tohidi等^[14]提出一种基于零空间的伪逆法（pseudo inverse along the null-space，PAN），作为一种特殊的再分配方法，PAN方法能有效处理各执行器的约束要求。Ma等^[15]在此基础上解决了执行量动态约束问题。

针对岸壁效应干扰的时变、强耦合和非线性特性，将借助复合正交神经网络（compound orthogonal neural network，CONN）在线学习补偿ESO估计误差部分，降低岸壁效应干扰对线性ESO在线估计的要求，并借助PAN综合考虑控制分配算法的实时性和精确性需求。在此基础上，在计及岸壁效应的船舶自主靠泊仿真环境中验证本文所提控制分配方法的有效性，并与基于广义逆和二次规划的经典控制分配方法进行对比分析。

1.   问题描述

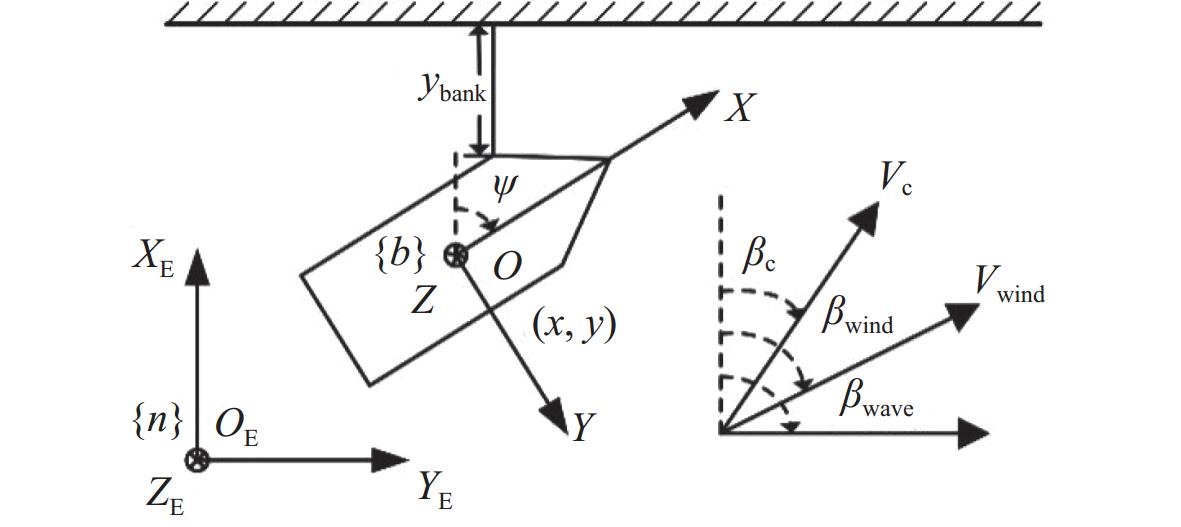
水面船舶通常只考虑纵荡、横荡和艏摇3个自由度运动，为便于描述船舶靠泊运动，如图2所示建立固定坐标系{n}和运动坐标系{b}。

图  2  固定坐标系与运动坐标系

Figure  2.  Definition of fixed and motion coordinate systems

下载: 全尺寸图片 幻灯片

船舶靠泊的运动学和动力学模型如下：

式中：${\boldsymbol{\eta }} = {{\text{[}}x,y,\psi {\text{]}}^{\text{T}}}$，为船舶在固定坐标系中定义的位置；${\boldsymbol{\nu }} = {{\text{[}}u,v,r{\text{]}}^{\text{T}}}$，为船舶在运动坐标系中定义的速度；${\boldsymbol{R}}\left( \psi \right) \in {{\bf{R}} ^{3 \times 3}}$，为两个坐标系间的转换矩阵；${\boldsymbol{M}} \in {{\bf{R}} ^{3 \times 3}}$和${\boldsymbol{D}} \in {{\bf{R}} ^{3 \times 3}}$分别为系统的惯性矩阵和阻尼矩阵；${{\boldsymbol{\tau }}_{\text{E}}} = {{\text{[}}{\tau _{{\text{E}u}}},{\tau _{{\text{E}v}}},{\tau _{{\text{E}r}}}{\text{]}}^{\text{T}}}$，为未知外界环境干扰，主要由风（风速为${V_{{\text{wind}}}}$，风向角为${\beta _{{\text{wind}}}}$）、浪（浪向角为${\beta _{{\text{wave}}}}$）、流（流速为${V_{\text{c}}}$，流向角为${\beta _{\text{c}}}$）以及岸壁效应产生；${\boldsymbol{\tau }} = {{\text{[}}{\tau _{\textit{u}}},{\tau _{\textit{v}}},{\tau _{\textit{r}}}{\text{]}}^{\text{T}}}$，为船舶推进系统产生的实际控制力。

对于过驱动配置的推进系统，需要找到可行推力解以满足上层控制器产生的三自由度控制指令，以推力最小为目标可以将控制分配模型构造为如下优化问题：

式中：${\boldsymbol{u}} = \left[ {{u_1}, \cdots ,{u_n}} \right] \in {\boldsymbol{U}} \subset {{\bf{R}} ^n}$，为n个推进器推力；${\boldsymbol{U}} = \left\{ {\left. {{u_i}} \right|{{\underline {u} }_i} \leqslant {u_i} \leqslant {{\bar u}_i}} \right\}(i = 1, \cdots ,n )$，为当前时刻推力可行域；${\underline {u} _i}$和${\bar u_i}$分别为第i个推进器的最小推力和最大推力，由推进系统物理限制决定；${{\boldsymbol{\tau }}_{\text{c}}} = {{\text{[}}{\tau _{{\text{c}u}}},{\tau _{{\text{c}v}}},{\tau _{{\text{c}r}}}{\text{]}}^{\text{T}}}$，为上层控制器下发的三自由度期望控制指令；${\boldsymbol{B}} \in {{\bf{R}} ^{3 \times n}}$，为配置矩阵，其中第i列为${{\boldsymbol{B}}_i} = {\left[ 1\;\;0\;\;{{l_i}} \right]^{\text{T}}}$或${{\boldsymbol{B}}_i} = {\left[ 0\;\;1\;\;{{l_i}} \right]^{\text{T}}}$，${l_i}$为第i个推进器相对船中心的位置。

根据Norrbin^[3]模型试验回归公式，构建岸壁效应模型如下：

式中：$\boldsymbol{Y}_{\text{s}}，\boldsymbol{N}_{\text{s}}$分别为离岸推力和艏吸力矩；$\rho$为海水密度；${C_{\text{b}}}$，${B_{\text{s}}}$，${L_{\text{s}}}$和d分别为船舶方形系数、船宽、垂线间长以及吃水；$V = \sqrt {{u^2} + {v^2}}$，为船舶速度；$S = {y_{{\text{bank}}}}\left( {\boldsymbol{\eta }} \right) + {{{B_{\text{s}}}} \mathord{\left/ {\vphantom {{{B_{\text{s}}}} 2}} \right. } 2}$，其中${y_{{\text{bank}}}}\left( {\boldsymbol{\eta }} \right)$为船舶到岸壁的最短距离，由位置${\boldsymbol{\eta }}$决定；h为港口水深。

本文的控制问题为：针对过驱动船舶靠泊运动模型（式（1））、控制分配模型（式（2）），考虑岸壁效应模型（式（3）），设计控制器和控制分配算法，使船舶在受到多源干扰时能准确跟随预设靠泊轨迹${{\boldsymbol{\eta }}_{\text{d}}}{\text{(}}t{\text{)}} = {{\text{[}}{x_{\text{d}}}{\text{(}}t{\text{)}},{y_{\text{d}}}{\text{(}}t{\text{)}},{\psi _{\text{d}}}{\text{(}}t{\text{)]}}^{\text{T}}}$，到达期望靠泊位置${\text{(}}{x_{{\text{d0}}}},{y_{{\text{d0}}}}{\text{)}}$，并调整艏向角至${\psi _{{\text{d0}}}}$，即控制目标为

式中：$\varepsilon$为正常数；$\left\| \cdot \right\|$为Euclid范数。

2.   基于零空间的自抗扰控制分配

2.1   自抗扰控制器设计

“先泊位外镇定再平行靠泊”策略通常依次设置镇定点和靠泊点作为期望位置，可以借助跟踪微分器（tracking differentiator，TD）进行过渡，缓和期望位置变化，如下所示：

式中：${{\boldsymbol{\eta }}_{{\text{td}}}}$为TD产生的参考期望位置；r为速度因子；${h_0}$为滤波因子；${f_{{\text{han}}}}{\text{(}} \cdot {\text{)}}$为最速控制综合函数。

船舶靠泊是一个由常速域到低速域的过程，水动力会随着船速变化而变化，惯性矩阵M和阻尼矩阵D可以表示如下：

式中：$\boldsymbol{M}_0和\boldsymbol{D}_{\text{0}}$为已知的标称惯性矩阵和阻尼矩阵；$\Delta\boldsymbol{M}和\Delta\boldsymbol{D}$为相应的未建模水动力不确定性矩阵。

由于推进系统物理限制，控制分配模块不能保证实际控制力${\boldsymbol{\tau }}$每一时刻都满足期望控制力${{\boldsymbol{\tau }}_{\text{c}}}$，可能会出现控制分配误差$\Delta {\boldsymbol{\tau }}{\text{(}}{{\boldsymbol{\tau }}_{\text{c}}},{\boldsymbol{\tau }}{\text{)}} = {\boldsymbol{\tau }} - {{\boldsymbol{\tau }}_{\text{c}}}$。

为简化描述和控制器设计，定义如下符号：

式中：${f_{\text{K}}}\left( {{\boldsymbol{\dot \eta }}} \right)$为系统已知动态；${f_{\text{E}}}\left( {{\boldsymbol{\eta }},{\boldsymbol{\dot \eta }}} \right)$为未知环境扰动；${f_{\text{U}}}\left( {{\boldsymbol{\eta }},{\boldsymbol{\dot \eta }},{{\boldsymbol{\tau }}_{\text{c}}},{\boldsymbol{\tau }}} \right)$为模型不确定和控制分配误差导致的系统未知动态；$d\left( {{\boldsymbol{\eta }},{\boldsymbol{\dot \eta }},{{\boldsymbol{\tau }}_{\text{c}}},{\boldsymbol{\tau }}} \right)$为待估计的系统集总不确定项。

由于$\psi {\text{(}}t{\text{)}}$，${\boldsymbol{\nu }}{\text{(}}t{\text{)}}$和${\boldsymbol{\dot R}}\left( {\psi {\text{(}}t{\text{)}}} \right)$均为连续函数，因此${f_{\text{K}}}\left( {{\boldsymbol{\dot \eta }}} \right)$关于${\boldsymbol{\dot \eta }}$满足全局Lipschitz条件，即$\exists {C_{\text{k}}} > 0$，满足$\left\| {{f_{\text{K}}}\left( {{{{\boldsymbol{\dot \eta }}}_1}} \right) - {f_{\text{K}}}\left( {{{{\boldsymbol{\dot \eta }}}_2}} \right)} \right\| \leqslant {C_{\text{k}}}\left\| {{{{\boldsymbol{\dot \eta }}}_1} - {{{\boldsymbol{\dot \eta }}}_2}} \right\|$。

假设 1：由于港口内作用于船舶的环境载荷以及船舶自身运动能量是有限的，系统总未知干扰$d\left( {{\boldsymbol{\eta }},{\boldsymbol{\dot \eta }},{{\boldsymbol{\tau }}_{\text{c}}},{\boldsymbol{\tau }}} \right)$对其所有自变量连续可微有界，即$\exists {C_{\text{h}}} > 0$，使其对时间的一阶导数$h\left( {{\boldsymbol{\eta }},{\boldsymbol{\dot \eta }},{\boldsymbol{\ddot \eta }},{{\boldsymbol{\tau }}_{\text{c}}},{\boldsymbol{\tau }}} \right)$满足$\left\| {h\left( {{\boldsymbol{\eta }},{\boldsymbol{\dot \eta }},{\boldsymbol{\ddot \eta }},{{\boldsymbol{\tau }}_{\text{c}}},{\boldsymbol{\tau }}} \right)} \right\| \leqslant {C_{\text{h}}}$。

对船舶靠泊数学模型式(1)～式(3)进行坐标转换，并令${{\boldsymbol{x}}_1} = {\boldsymbol{\eta }}$，${{\boldsymbol{x}}_2} = {\boldsymbol{\dot \eta }}$，重构模型如下：

为减轻ESO的估计负担，引入一种收敛性能优良、计算复杂度低的单隐藏层CONN在线逼近系统集总不确定项$d\left( \cdot \right)$。考虑岸壁效应和控制分配特性，定义${\boldsymbol{\xi }} = {\left[ {S\left( {{{\boldsymbol{x}}_1}} \right),{{\boldsymbol{x}}_2}^{\text{T}},{\boldsymbol{\tau }}_{\text{c}}^{\text{T}},1} \right]^{\text{T}}}$为网络输入：

式中：${\boldsymbol{\varPi }}$为逼近误差；${H_\xi } \subset {{\bf{R}} ^8}$，为网络输入${\boldsymbol{\xi }}$的可达集；${\boldsymbol{\sigma }} \in {{\bf{R}} ^q}$，为复合正交向量，其形式见文献[6]，其中q为隐藏层神经元数量；${{\boldsymbol{W}}^*} \in {{\bf{R}} ^{q \times 3}}$，为网络理想权值，应满足

令${{\boldsymbol{\hat x}}_1}$和${{\boldsymbol{\hat x}}_2}$分别为${{\boldsymbol{x}}_1}$和${{\boldsymbol{x}}_2}$的估计值，${\boldsymbol{\hat \xi }} = [ S\left( {{{{\boldsymbol{\hat x}}}_1}} \right), {{{\boldsymbol{\hat x}}}_2}^{\text{T}},{\boldsymbol{\tau }}_{\text{c}}^{\text{T}},1 ]^{\text{T}}$为${\boldsymbol{\xi }}$的估计值，${\boldsymbol{\hat W}}$表示网络输出权值，则CONN的输出为

根据式（9），将CONN估计误差视为ESO的扩张状态：

基于式（8）和式（12）设计如下NNESO：

式中：${{\boldsymbol{K}}_1}$，${{\boldsymbol{K}}_2}$和${{\boldsymbol{K}}_3} \in {{\bf{R}} ^{3 \times 3}}$，为ESO对角增益矩阵；${\gamma _{\textit{W}}}$和${K_{\textit{W}}}$为${\boldsymbol{\hat W}}$的正常数增益；${{\boldsymbol{\hat x}}_3}$为${{\boldsymbol{x}}_3}$的估计值；${\boldsymbol{y}} = {\boldsymbol{\eta }}$为传感器获取的船舶位置信息。

定义${{\boldsymbol{e}}_1} = {{\boldsymbol{\eta }}_{{\text{td}}}} - {{\boldsymbol{\hat x}}_1}$，${{\boldsymbol{e}}_2} = {{\boldsymbol{\dot \eta }}_{{\text{td}}}} - {{\boldsymbol{\hat x}}_2}$，在比例–微分（PI）反馈控制器的基础上，依据式(13)补偿未知扰动，设计如下控制律：

式中，${{\boldsymbol{K}}_{\text{p}}}$和${{\boldsymbol{K}}_{\text{d}}} \in {{\bf{R}} ^{3 \times 3}}$，为控制律增益矩阵。

2.2   零空间控制分配算法

对于式（2）的控制分配问题模型，可使用广义逆法求解：

式中，${{\boldsymbol{u}}_{\text{p}}} \in {{\bf{R}} ^n}$为控制分配问题的伪逆解。

广义逆法没有考虑推进系统的物理限制，当伪逆解${{\boldsymbol{u}}_{\text{p}}}$超出当前时刻的推力限幅${{\boldsymbol{u}}_{{\text{sat}}}}$时，可通过引入调整量${{\boldsymbol{u}}_{\text{n}}}$，在满足推力限幅的前提下，尽可能满足期望控制指令${{\boldsymbol{\tau }}_{\text{c}}}$。调整后的推力u为

推进系统实际产生的控制力${\boldsymbol{\tau }}$为

为保证等式约束能够成立，需满足${\boldsymbol{B}}{{\boldsymbol{u}}_{\text{n}}} = {\boldsymbol{0}}$。根据矩阵零空间性质，若配置矩阵B的一组零空间基为${\boldsymbol{N}} \in {{\bf{R}} ^{n \times 3}}$，对于线性组合的自由向量${{\boldsymbol{\tau }}_{\text{f}}}$有

定义${{\boldsymbol{u}}_{\text{p}}}$中超出${{\boldsymbol{u}}_{{\text{sat}}}}$的元素下标集合为k，为将k中对应的推力${{\boldsymbol{u}}_{{\text{p,}k}}}$调整至期望值${{\boldsymbol{u}}_{{\text{a,}k}}}$，结合式（18），选取${{\boldsymbol{\tau }}_{\text{f}}}$为

式中，${{\boldsymbol{N}}_{\textit{k}}}$由N中下标集合k对应的行组成，${{\boldsymbol{u}}_{{\text{a,}k}}}$的选取可以参见文献[15]。

结合式（15）～式（19），实际推力u可表示为

2.3   系统稳定性分析

定义${{\boldsymbol{\tilde x}}_i} = {{\boldsymbol{x}}_i} - {{\boldsymbol{\hat x}}_i}\left( {i = 1,2,3} \right)$和${\boldsymbol{\tilde W}} = {{\boldsymbol{W}}^{\text{*}}} - {\boldsymbol{\hat W}}$，根据式（8）～式（13），NNESO估计误差方程如下：

定义${\boldsymbol{\tilde X}} = {\left[ {{{{\boldsymbol{\tilde x}}}_1},{{{\boldsymbol{\tilde x}}}_2},{{{\boldsymbol{\tilde x}}}_3}} \right]^{\text{T}}}$，${\boldsymbol{\delta }} = f\left( {{{\boldsymbol{x}}_2}} \right) - f\left( {{{{\boldsymbol{\hat x}}}_2}} \right)$，式（21）则改写为如下紧凑形式：

其中：

由于A是Hurwitz的，必定存在一个正定矩阵${\boldsymbol{\varGamma }}$和一个正常数$\lambda$，满足

根据式（23）构造Lyapunov预选函数${V_1} = {{\boldsymbol{\tilde X}}^{\text{T}}}{\boldsymbol{\varGamma \tilde X}}$，可知${V_1}$是正定有界的，即${\lambda _{{\text{min}}}}\left( {\boldsymbol{\varGamma }} \right){\left\| {{\boldsymbol{\tilde X}}} \right\|^2} \leqslant {V_1} \leqslant {\lambda _{{\text{max}}}}\left( {\boldsymbol{\varGamma }} \right){\left\| {{\boldsymbol{\tilde X}}} \right\|^2}$。对${V_1}$求导，可得

由Young不等式可知，$\exists \kappa > 0$，满足

式中：${\omega _1} = {{\left( {{\lambda _{{\text{min}}}}\left( {\boldsymbol{\varGamma }} \right) - 2{C_{\text{k}}}\left\| {\boldsymbol{\varGamma }} \right\| - \kappa } \right)} \mathord{\left/ {\vphantom {{\left( {{\lambda _{{\text{min}}}}\left( {\boldsymbol{\varGamma }} \right) - 2{C_{\text{k}}}\left\| {\boldsymbol{\varGamma }} \right\| - \kappa } \right)} {{\lambda _{{\text{max}}}}\left( {\boldsymbol{\varGamma }} \right)}}} \right. } {{\lambda _{{\text{max}}}}\left( {\boldsymbol{\varGamma }} \right)}}$，且${\omega _1} > 0$；${\omega _2} = {{{{\left\| {{{\boldsymbol{B}}_2}{C_{\text{h}}}} \right\|}^2}{{\left\| {\boldsymbol{\varGamma }} \right\|}^2}} \mathord{\left/ {\vphantom {{{{\left\| {{{\boldsymbol{B}}_2}{C_{\text{h}}}} \right\|}^2}{{\left\| {\boldsymbol{\varGamma }} \right\|}^2}} \kappa }} \right. } \kappa }$。

定理 1：若假设1成立，$\exists \Im > 0$，当

则估计误差${\boldsymbol{\tilde X}}$一致最终有界，即$\mathop {{\text{lim}}}\limits_{t \to \infty } \left\| {{\boldsymbol{\tilde X}}{\text{(}}t{\text{)}}} \right\| \leqslant \Im$。

证明：对式（25）求解，两边开方，有

当$t \to \infty$时，$\exists \Im = \sqrt {{{{\omega _2}} / {{\omega _1}{\lambda _{{\text{min}}}}\left( {\boldsymbol{\varGamma }} \right)}}}$，满足$\| {{\boldsymbol{\tilde X}}} \| \leqslant \Im$。${\dot V_1} < 0$恒成立，定理1证毕。

将式（14）代入式（8），结合式（21），闭环自主靠泊控制系统的误差子系统可表示为

定义${\boldsymbol{E}} = {\left[ {{{\boldsymbol{e}}_1},{{\boldsymbol{e}}_2}} \right]^{\text{T}}}$，将式（27）改写为紧凑形式：

其中，

定理 2：若假设1和假设2及定理1成立，适当选取增益矩阵${{\boldsymbol{K}}_1}$，${{\boldsymbol{K}}_2}$，${{\boldsymbol{K}}_3}$，${{\boldsymbol{K}}_{\text{p}}}$和${{\boldsymbol{K}}_{\text{d}}}$，$\exists 0 < \vartheta < 1$，使得由式（22）和式（28）形成的闭环级联系统误差信号E一致最终有界，即

证明：选取Lyapunov函数${V_2} = {{{{\boldsymbol{E}}^{\text{T}}}{\boldsymbol{E}}} \mathord{\left/ {\vphantom {{{{\boldsymbol{E}}^{\text{T}}}{\boldsymbol{E}}} 2}} \right. } 2}$，对${V_2}$求导，得

根据定理1有$\left\| {{\boldsymbol{\tilde X}}} \right\| \leqslant \Im$，因此

由于C是负定矩阵，满足${\lambda _{{\text{max}}}}\left( {\boldsymbol{C}} \right) < 0$，因此

当$0 < \vartheta < 1$时，有

根据文献[16]可知，${\boldsymbol{E}}\left( t \right)$是有界的：

其中：${\gamma _0} = 2{\lambda _{{\text{max}}}}\left( {\boldsymbol{C}} \right)\left( {1 - \sigma } \right)$，$\varXi = - \dfrac{{\Im {{\left\| {\boldsymbol{D}} \right\|}_\infty }}}{{\vartheta {\lambda _{{\text{max}}}}\left( {\boldsymbol{C}} \right)}}$。

当$t \to \infty$时，满足$\left\| {\boldsymbol{E}} \right\| \leqslant \varXi$，因此误差信号E是一致最终有界的。定理2证毕。

若${{\boldsymbol{K}}_{\text{p}}}$，${{\boldsymbol{K}}_{\text{d}}}$足够大，${\lambda _{{\text{max}}}}\left( {\boldsymbol{C}} \right) \to \infty$， $\varXi \to 0$，${{\boldsymbol{e}}_1} \to {\boldsymbol{0}}$，${{\boldsymbol{e}}_2} \to {\boldsymbol{0}}$，即系统闭环误差一致渐近稳定。

3.   仿真实验与结果分析

3.1   仿真条件

为验证本文提出的基于零空间的自抗扰控制分配方法在船舶自主靠泊过程的有效性，以平台供应船Northern Clipper^[17]为模型进行先泊位外镇定再平行靠泊策略仿真实验。仿真模型水动力系数矩阵M，D和控制器标称水动力系数矩阵${{\boldsymbol{M}}_0}$，${{\boldsymbol{D}}_0}$见表1。

表  1  模型水动力系数

Table  1.  Coefficients of the model hydrodynamics

系数	数值
M	$\left[ {\begin{array}{*{20}{c}} {6.764\;4 \times {{10}^6}}&0&0 \\ 0&{1.134\;1 \times {{10}^7}}&{ - 3.401\;6 \times {{10}^7}} \\ 0&{ - 3.401\;6 \times {{10}^7}}&{4.452\;4 \times {{10}^9}} \end{array}} \right]$
D	$\left[ {\begin{array}{*{20}{c}} {7.703\;2 \times {{10}^4}}&0&0 \\ 0&{2.545\;5 \times {{10}^5}}&{ - 2.033\;1 \times {{10}^6}} \\ 0&{ - 6.722\;4 \times {{10}^5}}&{3.848\;1 \times {{10}^8}} \end{array}} \right]$
${{\boldsymbol{M}}_0}$	$\left[ {\begin{array}{*{20}{c}} {6 \times {{10}^6}}&0&0 \\ 0&{1 \times {{10}^7}}&{ - 3 \times {{10}^7}} \\ 0&{ - 3 \times {{10}^7}}&{4 \times {{10}^9}} \end{array}} \right]$
${{\boldsymbol{D}}_0}$	$\left[ {\begin{array}{*{20}{c}} {8 \times {{10}^4}}&0&0 \\ 0&{3 \times {{10}^5}}&{ - 2 \times {{10}^6}} \\ 0&{ - 7 \times {{10}^5}}&{4 \times {{10}^8}} \end{array}} \right]$

下载: 导出CSV 

| 显示表格

Northern Clipper的推进系统由2个主推、1个艏侧推、2个艉侧推及安装在艏部的全回转推进器组成。为提升船舶横向和艏向机动能力，固定全回转推进器方向，使其充当艏侧推。推进器配置如图3所示，各推进器参数见表2。

图  3  Northern Clipper推进器配置

Figure  3.  Configuration of Northern Clipper thruster

下载: 全尺寸图片 幻灯片

表  2  推进器参数

Table  2.  Parameter of the thruster

编号	距中心位置li /m	最大推力/kN	推力变化率/(kN·s−1)
1	4.65	1283.80	641.90
2	4.65	1283.80	641.90
3	34.39	268.52	134.26
4	32.10	268.52	134.26
5	24.69	725.20	362.60
6	33.07	268.52	134.26

下载: 导出CSV 

| 显示表格

为模拟真实靠泊环境，如图4所示，拟采用Jonswap波谱和Norsok风谱模拟海风和不规则风成波^[18]。采用本文给出的岸壁效应模型（式（3））模拟“岸推”、“岸吸”干扰，同时考虑海流影响，相关环境参数见表3。

图  4  海风和风成波

Figure  4.  Sea breeze and wind-waves

下载: 全尺寸图片 幻灯片

表  3  环境参数

Table  3.  Environmental parameters

参数	数值
风速$V_{\text{wind}}\text{/(m}\cdot\text{s}^{-1}\text{)}$	5.7
风向角$\beta_{\text{wind}}/(^{\circ}\text{)}$	−30
流速${V_{\text{c}}}/({\mathrm{m}}\cdot {\mathrm{s}}^{-1})$	0.2
流向角${\beta _{\text{c}}}/(^\circ )$	−60
平均波高${H_{{\text{wave}}}}/{\mathrm{m}}$	0.2
浪向角${\beta _{{\text{wave}}}}/{\text{(}}^\circ {\text{)}}$	−30
主波频率${\omega _{{\text{0wave}}}}/({\mathrm{rad}} \cdot {\mathrm{s}}^{-1})$	0.952

下载: 导出CSV 

| 显示表格

选取大连港老虎滩作为目的地。船舶初始位置和姿态设为${\eta }_{0}={\text{[500} \text{ m, 2 000}\text{ m, 0} ^\circ ]}^{\text{T}}$，初始速度设为${\nu }_{0}={\text{[0} \text{ m/s, 0} \text{ m/s, 0 } (^\circ) \text{/s]}}^{\text{T}}$，镇定位置和姿态设为${\eta }_{\text{k}}={\text{[2 095} \text{ m, 803} \text{ m, 29}\text{.2} ^\circ ]}^{\text{T}}$，靠泊位置和姿态设为${\eta }_{\text{b}}={\text{[1 706} \text{ m, 106} \text{ m, 29}\text{.2} ^\circ ]}^{\text{T}}$，泊位长为120 m，宽为25 m；采样步长设为1 s，仿真时长设为1 200 s。

为提高控制分配效率，设置控制器输出${{\boldsymbol{\tau }}_{\text{c}}}$限幅为${\text{[3}\text{.77}\times {\text{10}}^{\text{5}} \text{ N, 6}\text{.81}\times {\text{10}}^{\text{5}} \text{ N, 7}\text{.31}\times {\text{10}}^{6} \text{ N}\cdot \text{m]}}^{\text{T}}$，设置NNESO增益和控制律增益参数如表4所示。

表  4  控制器增益

Table  4.  Gains of the controller

参数	数值
${{\boldsymbol{K}}_1}$	${\text{diag}}\left( {\left[ {\begin{array}{*{20}{c}} {{\text{1}}{\text{.8}}}&{{\text{1}}{\text{.8}}}&{{\text{1}}{\text{.8}}} \end{array}} \right]} \right)$
${{\boldsymbol{K}}_2}$	${\text{diag}}\left( {\left[ {\begin{array}{*{20}{c}} {{\text{1}}{\text{.08}}}&{{\text{1}}{\text{.08}}}&{{\text{1}}{\text{.08}}} \end{array}} \right]} \right)$
${{\boldsymbol{K}}_3}$	${\text{diag}}\left( {\left[ {\begin{array}{*{20}{c}} {{\text{0}}{\text{.216}}}&{{\text{0}}{\text{.216}}}&{{\text{0}}{\text{.216}}} \end{array}} \right]} \right)$
$\gamma_{_{\mathrm{W}}}$	0.005
$K_{_{\mathrm{W}}}$	0.0002
${{\boldsymbol{K}}_{\text{p}}}$	${\text{diag}}\left( {\left[ {\begin{array}{*{20}{c}} {{\text{0}}{\text{.01}}}&{{\text{0}}{\text{.001}}}&{{\text{0}}{\text{.05}}} \end{array}} \right]} \right)$
${{\boldsymbol{K}}_{\text{d}}}$	${\text{diag}}\left( {\left[ {\begin{array}{*{20}{c}} {{\text{0}}{\text{.15}}}&{{\text{0}}{\text{.06}}}&{{\text{0}}{\text{.25}}} \end{array}} \right]} \right)$

下载: 导出CSV 

| 显示表格

在验证自抗扰控制器可行性的同时，将本文提出的ADRC-PAN控制分配方法与传统伪逆法（pseudo inverse，PI）^[9]和二次规划法（quadratic programming，QP）^[13]进行对比。

3.2   仿真实验结果分析

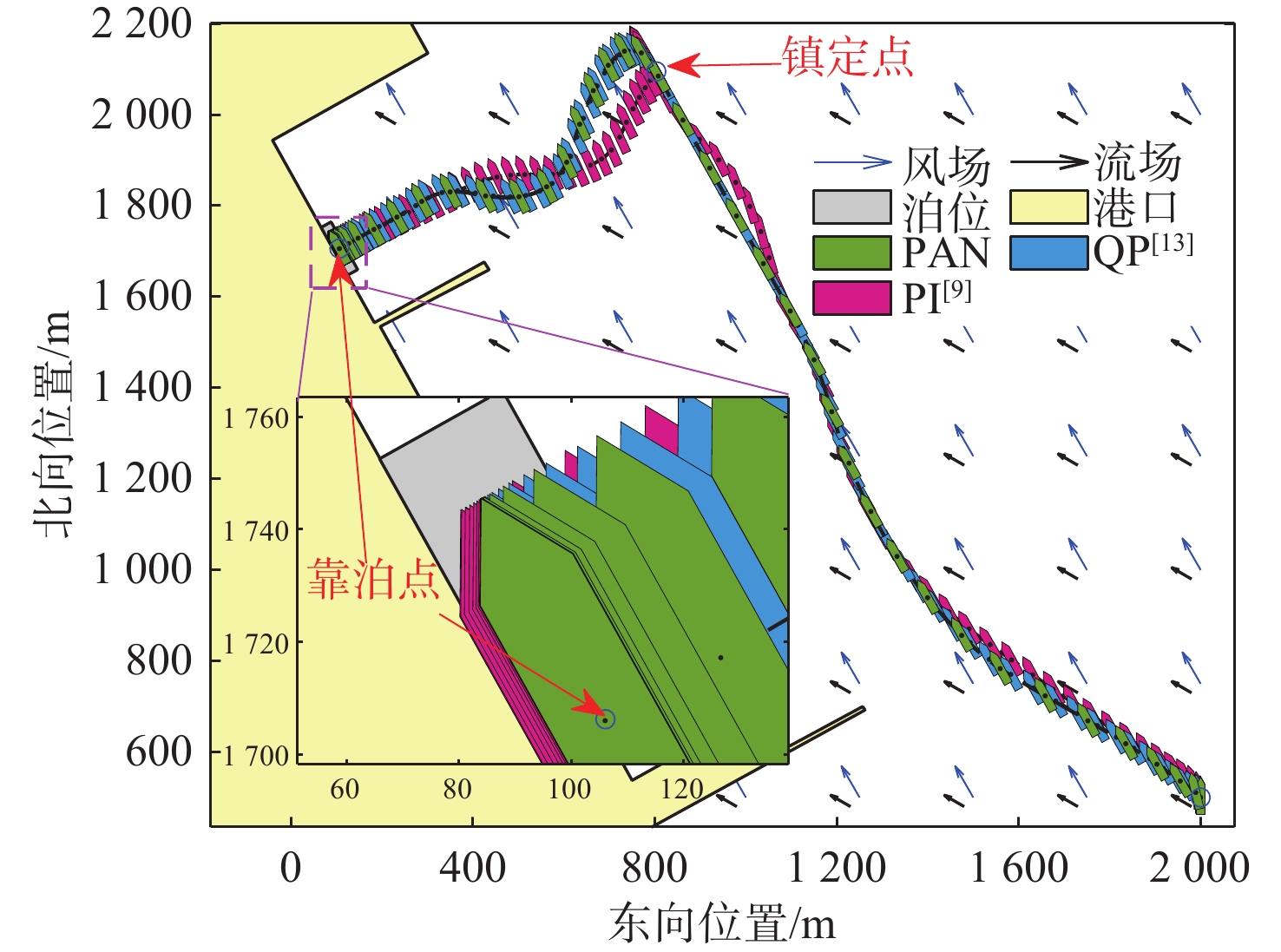
3种控制分配方法仿真对比结果如图5～图10所示。图5为船舶靠泊运动的轨迹和姿态变化，PI在抵达靠泊点后发生船首撞岸事故。而PAN和QP均能完成自主靠泊任务，依次通过镇定点和靠泊点，过程中无碰撞和撞岸现象。图6为固定坐标系下船舶的位置偏差图，PAN和QP的轨迹跟踪效果接近，在470 s时抵达镇定点，两段过程中位置误差收敛平缓，无明显超调现象；PI在600 s时抵达镇定点，靠泊用时较PAN和QP长，且艏向在镇定过程中有明显超调，结合下文图9，不难发现PAN在此时间段产生的较大控制分配误差是超调的主要原因。

图  5  PAN，QP和PI方法下靠泊轨迹与姿态变化图

Figure  5.  Trajectories and attitude changes using PAN, QP and PI methods

下载: 全尺寸图片 幻灯片

图  6  PAN，QP和PI方法下的位置偏差图

Figure  6.  Position errors obtained by PAN, QPM and PI methods

下载: 全尺寸图片 幻灯片

图  7  ADRC-PAN方法位置与速度估计图

Figure  7.  Estimated values of ship position and velocity via ADRC-PAN methods

下载: 全尺寸图片 幻灯片

图  8  ADRC-PAN方法扰动估计图

Figure  8.  Estimated values of disturbance via ADRC-PAN method

下载: 全尺寸图片 幻灯片

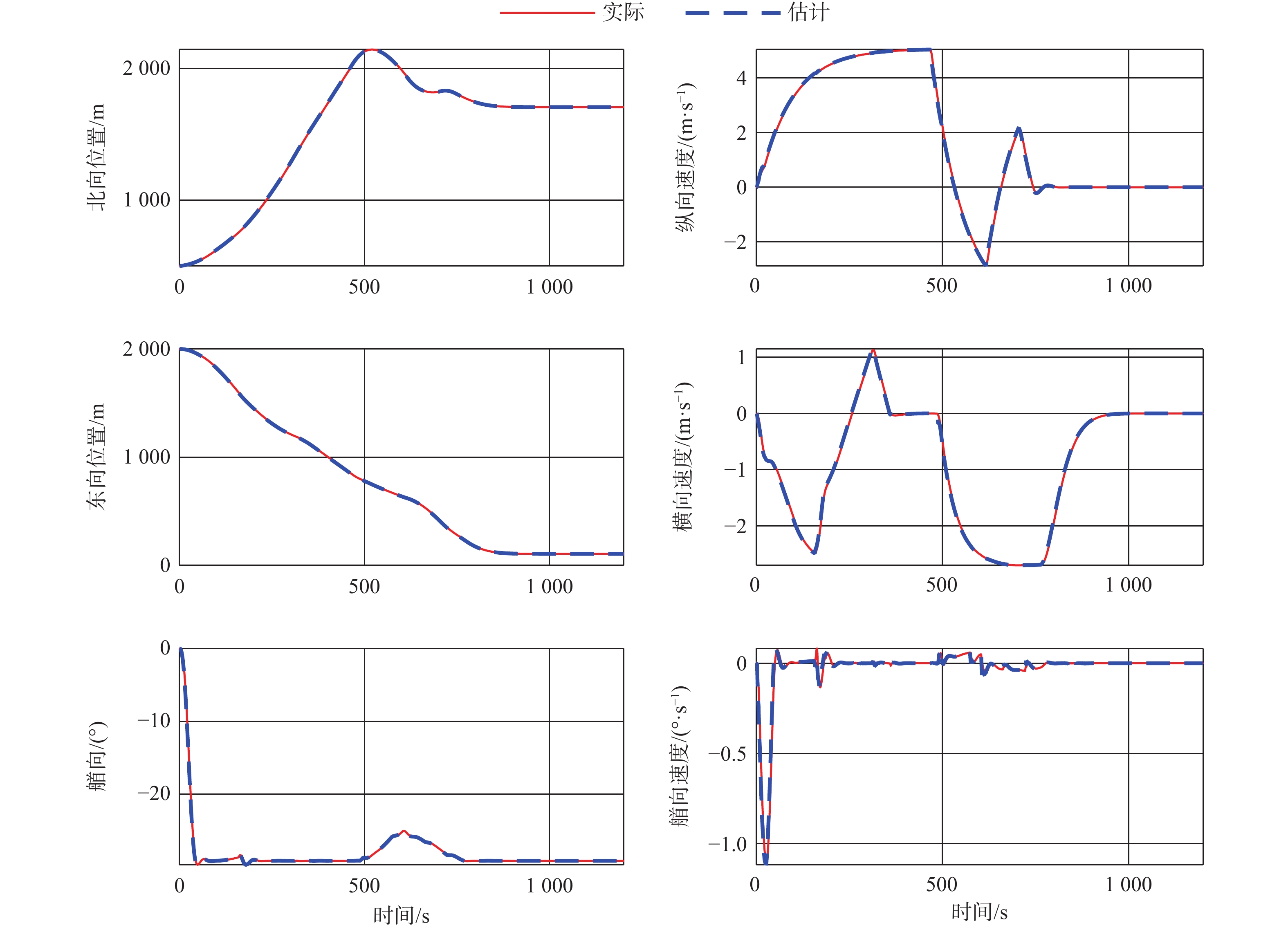
图7和图8分别为ADRC-PAN方法下NNESO对船舶位置、速度和集总不确定项的估计结果。由图7容易看出，即使仅依靠传感器的位置测量信息，ESO依然能较为准确地估计船舶实际位置和速度，且没有因控制分配误差产生较大的估计误差。从图8结果可知，在岸壁效应的影响下，ESO仍能在线估计船舶的集总不确定项，减小多源干扰的影响，为控制器提供可靠的输入。在800～900 s船舶接近岸壁过程中，得益于CONN的拟合能力，尽管出现抖振，仍能较准确地估计此时由岸壁效应主导的船舶扰动。结合图9，在第180 s和500 s附近，PAN产生的控制分配误差导致NNESO在相应时刻产生了较大的扰动估计误差，当控制分配误差消除后，扰动估计误差随后很快消除。

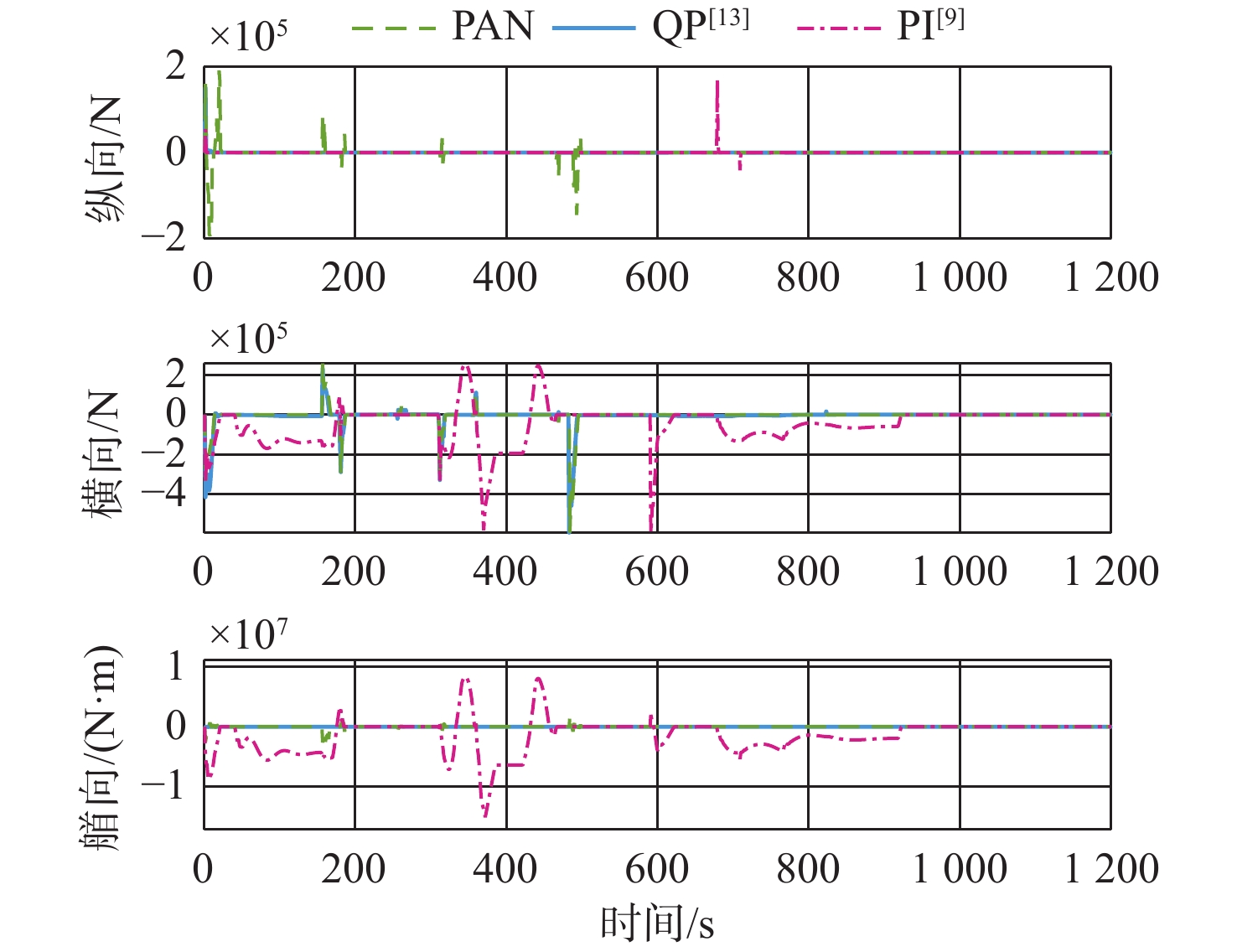
3种控制分配方法的分配误差如图9所示。纵荡上，由于靠泊过程对纵向速度的要求不高，除了初始和镇定时刻有瞬时误差外，3种方法均能准确完成控制分配任务。在横荡和艏摇上，由于PI没有考虑推进器物理限制，在0～200 s，300～450 s和600～900 s时段出现了较大的分配误差，结合图6不难看出这分别导致船舶在起步、镇定和近岸阶段中艏向误差抖振，同时也是图5中PI近岸时发生船首撞岸的主要原因。PAN和QP由于推进系统横向推进能力较弱，在起步和抵达镇定点后会导致一定的分配误差，且PAN较QP的分配误差略大。总体而言，PAN的精确性略逊于QP，但是优于PI。

图  9  PAN，QP和PI方法下控制分配误差图

Figure  9.  Control allocation errors via PAN, QP and PI methods

下载: 全尺寸图片 幻灯片

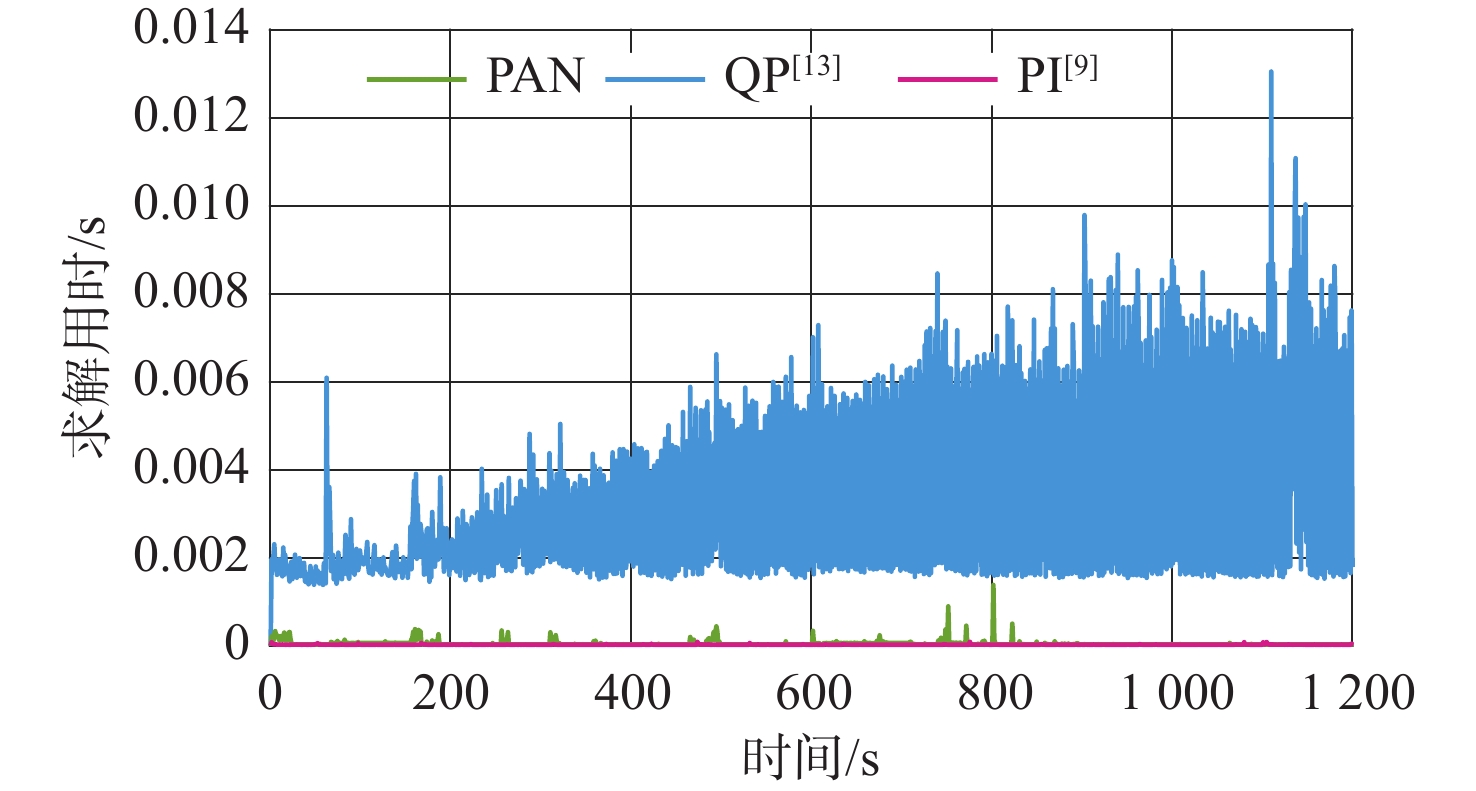
图10是单次步长求解用时，可以看出，PI与PAN求解所需时间相当且远小于QP所需时间，PAN的实时性优于QP。

图  10  PAN，QP和PI方法下单次步长求解用时

Figure  10.  Time-consumption for single-step solution via PAN, QP and PI methods

下载: 全尺寸图片 幻灯片

3种控制分配方法在计算时间${T_{{\text{comp}}}}$、平均控制分配误差${\delta _{{\text{AAE}}}}$和最大绝对误差${\delta _{{\text{MAE}}}}$上的对比结果见表5。各指标计算公式如下^[19]：

表  5  PAN，QP和PI控制分配方法对比

Table  5.  Results comparison of the control allocation methods of PAN, QP and PI

比较项	PI	PAN	QP
${T_{{\text{comp}}}}{\text{/s}}$	0.0293	0.0537	4.1519
${\delta _{{\text{AAE}}u}}/{\text{N}}$	242.61	3253.10	236.22
${\delta _{{\text{AAE}}v}}/{\text{N}}$	6.00×104	7.80×103	1.01×104
${\delta _{{\text{AAE}}r}}/\left( {{\text{N}} \cdot {\text{m}}} \right)$	1.86×106	4.99×104	1.04×102
${\delta _{{\text{MAE}}u}}/{\text{N}}$	1.70×105	2.67×105	1.51×105
${\delta _{{\text{MAE}}v}}/{\text{N}}$	5.93×105	5.92×105	5.92×105
${\delta _{{\text{MAE}}r}}/\left( {{\text{N}} \cdot {\text{m}}} \right)$	1.52×107	5.55×106	6.14×104

下载: 导出CSV 

| 显示表格

式中，${S_{{\text{CA}}}}{\text{(}}t{\text{)}}$为控制分配算法单次步长求解时间。

由${T_{{\text{comp}}}}$可以看出，本文所用方法的计算时间与伪逆法接近，仅为二次规划法所需时间的1.3%；由${\delta _{{\text{AAE}}r}}$和${\delta _{{\text{MAE}}r}}$可知，本文所用方法在艏向上的平均分配误差和最大分配误差分别仅为伪逆法的2.6%和36.51%。由此可见，本文所用方法能够兼顾对控制分配算法的精确性和实时性要求。

4.   结　论

经过理论分析和仿真对比实验，得到以下结论：

1) 本文所提出的NNESO对时变、强耦合、非线性的岸壁效应干扰以及风、浪、流等干扰有较好的在线估计效果，为控制器提供了可靠的输入。

2) 零空间控制分配方法基于伪逆法设计，仍属解析法，通过牺牲较短的时间提升控制分配的精确性，1200个仿真周期控制分配模块求解仅需0.0537 s。此外，平均和最大艏向控制分配误差相较伪逆法误差大幅减小，且轨迹跟踪结果与二次规划法接近。在船舶靠泊中，零空间方法能在实时性和精确性之间取得较好的平衡。

3) 基于零空间的自抗扰控制器在船舶自主靠泊中有较好的表现，在合理选取镇定点和靠泊点的前提下能够快速、稳定地完成靠泊任务。

综上所述，对于船舶自主靠泊，本文提出的基于零空间的自抗扰控制分配方法在保证靠泊安全性的前提下可降低船舶主控计算负荷，具有较大的应用潜力。该方法在简化的泊位形式中已有良好表现，更为复杂和真实的港口环境下的靠泊以及港内避碰是继续研究的重点。