Dynamic and tribological coupling analysis of journal bearing based on dynamic substructure
-
摘要:目的 分析主轴承的动力学与摩擦学特性以及其相互耦合关系。方法 首先,利用子结构法建立轴承磨损试验台耦合摩擦特性的动力学模型;然后,通过该动力学模型计算得到轴承摩擦耗功和轴心轨迹并与实测结果进行比较,验证模型的正确性;最后,在该模型的基础上进行主轴承摩擦学和动力学的耦合分析。结果 结果显示,试验台的4个支撑轴承均处于液动润滑状态,被测轴承在上止点处于混合润滑状态;随着轴承间隙的增大,轴承试验台被测轴承最小油膜厚度先增大后减小,当间隙在20 μm左右时可以得到最佳润滑状态;相比非线性弹簧的油膜模型,采用EHD模型可得到精度更高的轴承载荷和摩擦功耗。结论 研究结果可为轴承副的润滑性能设计和高精度建模提供理论指导。Abstract:Objectives This paper studies the dynamic and tribological characteristics of the main journal bearing, and the coupling relationship between them.Methods First, a dynamic model of the coupling tribological properties of a bearing wear test bed is established using the substructure method. The friction power consumption and orbital paths of the bearing are then calculated and compared with the measured results to verify the accuracy of the model. Finally, based on the model, the dynamic and tribological coupling analyses of the bearing are carried out.Results The results show that the four support bearings of the test bed are in a state of hydrodynamic lubrication, while the tested bearing is in a state of mixed lubrication at the top dead center. With the increase in radial clearance, the minimum oil film thickness of the tested bearing increases first and then decreases, and the most optimal lubrication state can be obtained when the tested bearing clearance is about 20 μm. Compared with the oil film model of a nonlinear spring, the elastohydrodynamic model can provide bearing load and friction power consumption results with higher accuracy.Conclusions The results of this study can provide theoretical guidance for the lubrication performance design and high-precision modeling of bearing pairs.
-
Keywords:
- journal bearing /
- dynamic property /
- substructure /
- tribology /
- coupling
-
0. 引 言
滑动轴承被广泛应用于舰船等各类机械系统中,作为主要的运动副和激励源,它是功率损耗和振动的主要来源之一,动力学及摩擦学特性对其性能及可靠性影响很大[1-2]。因此,对滑动轴承摩擦学和动力学特性进行试验与计算分析具有重要意义。滑动轴承摩擦学和动力学性能研究的3个最重要因素是运动部件的动力学特性、接触面间的摩擦学特性以及其试验验证,但基于有限元法的建模往往会产生较多的自由度,而接触面的摩擦特性也会引入非线性从而导致计算资源消耗的进一步增加。此外,针对发动机内部的轴承的试验条件比较苛刻[3-4]。
常规的有限元离散化法由于会产生过多的自由度而导致求解十分困难,为了在保持计算精度的同时考虑油膜的非线性,近年来发展了动态子结构法,即在建立复杂结构系统力学模型时,从量级上大幅缩减整体结构的自由度,从而保证计算精度[5-7]。针对轴颈和轴瓦间的油膜作用,基于Hertz接触模型提供了一种简化的非线性计算方法[8]。Greenwood等[9]和Patir等[10]分别对弹性粗糙表面的粗糙接触机理和粗糙表面间的油膜动压润滑机理进行研究,得到了Greenwood/Tripp粗糙接触模型和基于平均流量系数的弹性流体动力润滑(EHD)模型,奠定了弹性流体动力润滑理论基础。Bukovnik等[11]等比较了不同类型滑动轴承仿真模型和油液润滑条件的影响。卢伯聪等[12]对主轴承热弹性流体动力润滑(TEHD)进行研究,并在TEHD求解中考虑了轴瓦热效应的影响,从理论上更接近轴承实际的工作状态,但相关研究主要集中在理论计算分析层面,缺乏试验数据的支撑。
本文拟采用仿真与试验相结合的方法,首先基于子结构法建立各零部件的体单元,并通过EHD模型考虑连接副的摩擦学特性,进而建立考虑滑动轴承油膜作用的多柔性体主轴承磨损试验台动力学模型;接着,进行动力学和摩擦学的仿真计算并与试验结果进行对比分析,验证计算方法的正确性,然后在此基础上揭示轴承转子系统的动力学与摩擦学耦合机理;最后,对比基于非线性弹簧模型和EHD模型的计算精度,进而得到主轴承热弹性流体润滑计算的精确建模方法。
1. 基本理论
1.1 动态子结构缩减理论
采用有限元方法求解往往会产生规模巨大的离散化模型,加大了求解的难度。子结构法是通过将结构由整体划分为简单的子结构,然后基于特定的算法(静态缩减、古典动态子结构法、约束模态综合法或自由模态综合法等)将原本的大自由度系统缩减为保留主自由度及包含质量、刚度、恢复矩阵的子结构模型。静态缩减往往会使固有频率偏高,且其假设低频段惯性力对副自由度的影响比静力效应小,因此在多体系统动力学中,采用动态缩减进行求解的精度更高,其运动方程为[12]:
\begin{split} \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{M}}_{mm}}}&{{{\boldsymbol{M}}_{ms}}} \\ {{{\boldsymbol{M}}_{sm}}}&{{{\boldsymbol{M}}_{ss}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\ddot {\boldsymbol{x}}}_m}} \\ {{{\ddot {\boldsymbol{x}}}_s}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{K}}_{mm}}}&{{{\boldsymbol{K}}_{ms}}} \\ {{{\boldsymbol{K}}_{sm}}}&{{{\boldsymbol{K}}_{ss}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{x}}_m}} \\ {{{\boldsymbol{x}}_s}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{f}}_m}} \\ 0 \end{array}} \right]\\ \end{split} (1) 式中:M,K分别为模型的质量和刚度矩阵;x,f 分别为位移和力矢量;下标m,s 分别为主自由度和副自由度的坐标。
由式(1)中的第2个方程式,可以得到
({{\boldsymbol{M}}_{sm}}{\ddot {\boldsymbol{x}}_m} + {{\boldsymbol{M}}_{ss}}{\ddot {\boldsymbol{x}}_s}{\text{) + (}}{{\boldsymbol{K}}_{sm}}{{\boldsymbol{x}}_m} + {{\boldsymbol{K}}_{ss}}{{\boldsymbol{x}}_s}) = 0 (2) 其解为:
{{\boldsymbol{x}}}_{s}=-({{\boldsymbol{K}}}_{ss}-{\lambda }^{2}{{\boldsymbol{M}}}_{ss}{)}^{-1}{{\boldsymbol{K}}}_{sm}{{\boldsymbol{x}}}_{m} (3) 取其第i阶特征值λj2的值Pj进行计算,式(3)变为
\left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{x}}_m}} \\ {{{\boldsymbol{x}}_s}} \end{array}} \right\}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {\boldsymbol{ I}} \\ { - {{({{\boldsymbol{K}}_{ss}} - {P_j}{{\boldsymbol{M}}_{ss}})}^{ - 1}}{{\boldsymbol{K}}_{sm}}} \end{array}} \right]\left\{ {{{\boldsymbol{x}}_m}} \right\} = {{\boldsymbol{T}}_s}{{\boldsymbol{x}}_m} (4) 式中:I为单位矩阵;
{{\boldsymbol{T}}_s} 为坐标转换矩阵。将式(4)代入式(1),变换后缩减模型的运动方程为{{\boldsymbol{M}}_{\rm{R}}}{\ddot {\boldsymbol{x}}_m} + {{\boldsymbol{K}}_{\rm{R}}}{{\boldsymbol{x}}_m} = {{\boldsymbol{f}}_{\rm{R}}} (5) 式中,
{{\boldsymbol{M}}_{\rm{R}}} = {\boldsymbol{T}}_s^{\text{T}}{\boldsymbol{M}}{{\boldsymbol{T}}_s} ,{{\boldsymbol{K}}_{\rm{R}}} = {\boldsymbol{T}}_s^{\text{T}}{\boldsymbol{K}}{{\boldsymbol{T}}_s} ,{{\boldsymbol{f}}_{\rm{R}}} = {\boldsymbol{T}}_s^{\text{T}}\left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{f}}_m}} \\ 0 \end{array}} \right\} ,分别为缩减模型的质量、刚度矩阵和力矢量,模型的自由度下降。1.2 Greenwood/Tripp粗糙接触模型
随着供油条件变差,当油膜厚度减小至一定程度时,两粗糙表面间部分微凸体直接接触,从而产生较大的摩擦力。针对这种现象,Greenwood等[9]提出了一种考虑表面粗糙形貌名义平面的弹性接触理论,得到了接触变形与表面形貌的相互关系。对于微凸体高度呈标准正态分布的表面,根据Greenwood/Tripp粗糙接触理论,微凸体接触压力
{p_{\rm{a}}}(h) 为{p_{\text{a}}}\left( h \right) = K{E'}{{\boldsymbol{F}}_{\frac{5}{2}}}\left( {{H_{\rm{s}}}} \right) (6) {H_{\rm{s}}} = \frac{{h - {{\bar \delta }_{\rm{s}}}}}{\sigma } (7) E^{\prime}=\frac{1}{\dfrac{1-\varepsilon_{1}^{2}}{E_{1}}+\dfrac{1-\varepsilon_{2}^{2}}{E_{2}}} (8) {F}_{\frac{5}{2}}({H}_{{\rm{s}}})=\left\{ \begin{aligned} & 4.408\;6\times {10}^{-5}{\left(4-{H}_{{\rm{s}}}\right)}^{6.804},\;{H}_{{\rm{s}}} < 4\\& \qquad\qquad0,\qquad\qquad\quad\;\;\;{H}_{{\rm{s}}}\geqslant 4 \end{aligned} \right. (9) 式中:K为弹性因子;E'为等效弹性模量,Pa;Hs为无量纲凸峰间隙;h为润滑油名义油膜厚度,m;
{\overline \delta _{\rm{s}}} 为平均凸峰高度,m;σ为两接触表面综合粗糙度,m;ε1,ε2分别为两接触面材料的泊松比;E1,E2为两接触面材料的弹性模量,Pa。1.3 粗糙接触表面平均雷诺方程
联立流体连续性方程和运动方程(Navier-Stokes方程),假设滑油密度、粘度在油膜厚度方向为常值,可得到简化后的一般形式为雷诺方程。为了考虑流体膜厚度达到与固体表面粗糙度接近的数量级时表面微观形貌对润滑性能的影响,以一般形式的雷诺方程为基础,Patir等[10]引入了压力流量系数、剪切流量系数概念,得到平均雷诺方程为
\begin{split} & - \frac{\partial }{{\partial x}}\left( {\theta {\phi _x}\frac{{\rho {h^3}}}{{{\text{12}}\eta }}\frac{{\partial p}}{{\partial x}}} \right) - \frac{\partial }{{\partial {\textit{z}}}}\left( {\theta {\phi _{\textit{z}}}\frac{{\rho {h^3}}}{{{\text{12}}\eta }}\frac{{\partial p}}{{\partial {\textit{z}}}}} \right){\text{ + }}\\&\qquad\frac{\partial }{{\partial x}}\left( {\theta \rho (\bar h + \sigma {\phi _{\text{s}}})\frac{U}{2}} \right) + \frac{{\partial \left( {\theta \rho \overline h } \right)}}{{\partial t}} = 0 \end{split} (10) 式中:x,z分别为轴向和径向坐标轴;
\phi_x ,\phi_{\textit{z}} 分别为x,z向压力流量系数;ρ为流体密度,kg/m3;η为机油粘度,mPa·s;\overline h 为油膜平均厚度,m;p为油膜压力,Pa;θ为机油填充率;U为轴颈表面线速度,m/s;\phi_{\rm{s}} 为剪切流量系数;t为时间,s。1.4 EHD数学模型的计算流程
基于动态子结构弹性流体动力润滑(EHD)的计算需联立能量方程、平均雷诺方程、弹性位移方程及载荷平衡方程,并进行求解[8]。其中,能量方程、弹性位移方程采用有限元法求解;平均雷诺方程采用有限差分法求解,且差分网格由轴瓦内表面的缩减模型主自由度节点决定。在计算过程中,采用平均雷诺方程求解得到油膜压力(包含粗糙接触产生的接触压力)后代入弹性位移方程,从而得到各个节点的弹性位移和油膜厚度并迭代至收敛。其计算流程如图1 所示。
2. 轴承磨损试验台EHD建模
基于动态子结构缩减理论,利用AVL_Excite Power Unit模块,以轴承磨损试验台为研究对象进行轴承热弹性流体润滑特性分析。轴承磨损试验台主要包含驱动电机、传动轴系、扭矩传感器、被测单元以及液压和供油系统。其中被测单元包含2个支撑轴承座(每个轴承座含2个支撑轴承)、1个被测轴及连杆;驱动电机通过传动轴为被测单元的被测轴提供转速边界条件;液压系统通过液压缸将载荷施加于连杆;供油系统为系统各轴承提供稳定的供油边界条件。轴承磨损试验台的三维结构如图2所示,其基本参数如表1所示。
表 1 轴承磨损试验台主要参数Table 1. Main parameters of bearing wear test bed参数 数值 参数 数值 轴承宽度b/mm 29 油孔位置/(°) 45 轴颈直径/mm 52.68 油孔直径/mm 4 径向(半径)间隙c/μm 250 进油温度/℃ 55 支撑轴瓦1(半径)间隙c1/μm 50 进油压力/bar 9 支撑轴瓦2(半径)间隙c2/μm 50 轴颈表面粗糙度/μm 0.4 润滑油牌号 10W-30 轴瓦表面粗糙度/μm 0.5 2.1 多体动力学建模
在实际工作中,除被测单元外,其他部件无宏观运动,建模时,只需将被测部分的固定件和运动件视为柔性体,液压载荷以外载荷形式输入,右侧电机的作用通过右侧节点的恒定转速进行考虑即可。试验台包含两侧的支撑座共4个滑动轴承以及被测轴承,因此,所建的动力学模型包含2个轴承座和被测偏心轴以及连杆体单元,其中在偏心轴与各轴承座之间建立2个EHD连接副,在偏心轴与连杆之间建立1个EHD连接副,得到的多体系统动力学模型如图3所示。
2.2 缩减模型的建立
偏心轴和连杆是轴承磨损试验台多体系统动力学模型的主要运动部件,其动力学特性的准确性将直接影响计算结果的精度。为了提高计算效率,采用自由界面子结构法(Craig-Chang法)建立了缩减模型,如表2所示。为了保证缩减模型的动力学特性与有限元模型一致,分别对有限元模型和缩减模型进行了模态计算,其各阶模态频率的对比如表3和表4所示。经对比分析可知,偏心轴、连杆缩减体的各阶模态频率与有限元模型的误差不超过2%,说明缩减模型与有限元模型的动力学特性基本一致。
表 2 主要零部件有限元模型与缩减模型Table 2. Finite element model and condensed model of main parts零部件 有限元模型 缩减模型 偏心轴 

支撑轴承座 

连杆 
 表 3 偏心轴有限元模型与缩减模型模态对比Table 3. Comparison of modal frequency between finite element models and condensed model of eccentric shaft
表 3 偏心轴有限元模型与缩减模型模态对比Table 3. Comparison of modal frequency between finite element models and condensed model of eccentric shaft阶数 频率/Hz 误差/% 振型 有限元模型 缩减模型 1 1 708.5 1 710.5 0.117 YZ 面内弯曲模态 2 1 718.7 1 721.7 0.175 XZ 面内弯曲模态 3 4 021.6 4 020.4 −0.030 扭转模态 4 4 332.6 4 344.5 0.275 YZ 面内弯曲模态 5 4 360.8 4 362.9 0.048 XZ 面内弯曲模态 表 4 连杆有限元模型与缩减模型模态对比Table 4. Comparison of modal frequency between finite element model and condensed model of connecting rod阶数 频率/Hz 误差/% 振型 有限元模型 缩减模型 1 963.5 963.23 −0.03 XZ 面内弯曲模态 2 1 213.6 1 212.4 −0.10 扭转模态 3 1 558.6 1 554.6 −0.26 YZ 面内弯曲模态 4 1 816.4 1 814.4 −0.11 小端局部模态 5 2 644.1 2 645.1 0.038 扭转模态 3. 试验验证及结果分析
3.1 测试系统
为了验证计算模型的正确性,在轴承磨损试验台布置了相应的测点进行试验数据采集。首先,通过扭矩仪间接测量轴承的摩擦功耗,如图2所示。图4(a)所示为主要测点布置图。在连杆两侧伸出的结构上安装夹角为90°的位移传感器,用于测量轴心轨迹,其原理如图4(b)所示,轴承磨损试验台的测量参数如表5所示。
表 5 轴承磨损试验台主要测试参数Table 5. Main test parameters of bearing wear test bed传感器 信号类型 被测对象 位移传感器 位移 轴心轨迹 扭矩仪 扭矩 摩擦功耗 温度传感器 温度 瓦背温度 压力传感器 压力 供油压力 3.2 计算结果验证与分析
3.2.1 结果验证
模型的验证从2个方面进行:1)对比360°曲柄转角内轴承磨损试验台摩擦力扭矩的计算值与试验值,验证其摩擦学特性;2)对比计算与试验所得的轴心轨迹,验证轴承磨损试验台模型转子的动力学特性,如图5所示。
经对比发现,试验测得的扭矩值大于计算值,这是因为试验台在安装过程中存在一定的轴系不对中情况,产生了部分阻力,且自由端储存的滑油也会对轴产生拖拽力矩,不过在摩擦力力矩方面计算值与试验值的误差在10%以内;计算所得与试验测得的轴心轨迹轮廓及位置基本一致,验证了该计算模型在摩擦学及动力学上的正确性。
3.2.2 结果分析
运用本文第2节的建模方法,建立包含5个轴承的轴承磨损试验台EHD多体系统动力学模型,按X方向,从左到右,各轴承号分别为1#~5#。在验证模型精度的基础上,对各轴承的润滑特性进行计算分析。表6对比列出了5个轴承在3 000 r/min工况下的最大油膜压力pmax、最小油膜厚度hmin、最小膜厚比λ、一周期内平均粗糙接触比例γ及摩擦功耗Wm。
表 6 各轴承EHD润滑计算结果Table 6. EHD calculation results of diffrent bearings of the test bed轴承号 性能参数 pmax /MPa hmin /μm λ γ/% Wm /W 1 2.87 20.87 32.61 0 241.74 2 16.51 8.07 12.61 0 318.92 3 106.78 1.38 2.03 1.42 486.89 4 16.49 8.07 12.61 0 319.03 5 2.68 20.89 32.64 0 248.67 由表6可知,1#~5#轴承的润滑状态参数关于3#轴承(被测轴承)对称,被测轴承承受了最大的载荷,且最大油膜压力较其他4个支撑轴承高出一个量级,最小油膜厚度达到了综合粗糙度量级,使得膜厚比偏小,出现了局部粗糙接触。根据Stribeck曲线[13],两侧支撑轴承最小膜厚比大于10,处于完全液动润滑状态,而被测轴承则处于混合摩擦状态,轴颈与轴瓦间的粗糙接触比例和摩擦功耗呈现相同的规律。被测轴承最小油膜厚度出现的时刻与活塞上的止点相对应,此时,倒置的连杆处于最高位置,下轴瓦与偏心轴表面接触,液压系统对连杆施加的载荷处于峰值。由于支撑轴承的数量为被测轴承的4倍,单个轴承的轴瓦承受的载荷远小于被测轴承下瓦,此时,被测轴承下瓦的油膜压力远大于支撑轴承的油膜压力,且轴颈与轴瓦间出现了部分粗糙接触,产生了粗糙接触压力,进而使轴瓦进入混合润滑状态,粗糙接触比例增高,摩擦功耗增高。
分别提取5个轴承在被测轴承产生最小油膜厚度时刻的油膜总压和粗糙接触压力,其分布图分别如图6和图7所示。由图中不难发现,最外侧固定支撑轴承的油膜压力的分布梯度要小于中间支撑轴瓦的油膜压力分布梯度。另由图7所示粗糙接触压力分布彩图,发现支撑轴瓦无粗糙接触压力,说明即便是处于最恶劣的工况,支撑轴瓦仍可保持热动润滑状态,而被测轴瓦下瓦的两侧则出现了局部粗糙接触。
由上述分析可知,被测的3#轴承其润滑条件最差。为了解其润滑特性,分析不同间隙被测轴承的动力学及摩擦学特性,对比了不同间隙(1~1 000 μm)下,一个周期内的最大油膜压力、最小油膜厚度和平均摩擦功耗。
由图8(a)和图8(b)可以看出,随着半径间隙的增大,轴承最大油膜压力随之升高,但最小油膜厚度在一定范围内是先增大后减小,当半径间隙达20 μm时,最小油膜厚度达到峰值,摩擦功耗最低。当半径间隙非常小时,轴颈与轴瓦间出现微凸体接触,轴承处于边界润滑状态,不易形成足够厚的油膜,而随着间隙的增大,最小油膜厚度逐渐增大,油膜支撑力增强,但当间隙过大时,在端泄的作用下,油膜支撑能力将下降,最小油膜厚度也随之下降。同理,摩擦功耗在半径间隙非常小的时候因边界润滑摩擦系数较大,随着间隙的增大逐渐处于液动润滑状态,摩擦力下降;而当间隙过大时,液动润滑剪切应力会升高,同时由于油膜支撑力下降,局部出现的粗糙接触也会导致摩擦功耗上升。
间隙为10和1 000 μm这2种工况下的轴承总摩擦功耗及轴承载荷如图9所示。由图可知,两种工况下的轴承载荷比较接近,但在载荷极值处,即液压系统载荷峰值处,后者较前者力的幅度增大了几百牛,总摩擦耗功也同样从10 μm时的0 W上升到了几百瓦,且摩擦功耗峰值点与载荷极值点对应,说明间隙过大产生的冲击导致局部润滑状态突变,进而使摩擦功耗增加。
3.3 不同建模方式计算结果对比
由上节分析可知,轴承动力学与摩擦学之间存在较强的耦合关系。除上节叙述的通过求解平均雷诺方程进行轴承动力学分析之外,轴承油膜的建模还有其他常用方法,比如简化的非线性弹簧单元,即将轴颈和轴瓦间的高压油膜简化为轴颈与轴瓦间的若干非线性弹簧阻尼单元,求解时,通过激活处于压缩状态的弹簧来迭代计算得到相应的弹簧力,进而得到轴承载荷。为了对比基于EHD模型和非线性弹簧模型建模方法的差别,在相同动力学模型的基础上修改被测轴承连接副的单元类型为非线性弹簧单元并进行计算。将非线性弹簧单元与不同间隙EHD连接副算得的被测试验台轴承动力学、摩擦学结果进行对比,其时域图如图9(b)所示。由图中不难发现,当轴承间隙较小时,采用非线性弹簧模型与EHD模型计算得到的轴承载荷基本一致,但随着轴承间隙的增大,油膜因端泄的作用其支撑力下降;轴颈与轴瓦冲击的增大在载荷时域图中表现为明显的波动。非线性弹簧不存在实际工况中可能出现的冲击现象,采用计算得到的结果在间隙较大的情况下依然是较顺滑的载荷曲线,这与实际工况差异较大。对采用2种建模方法计算得到的轴承载荷进行了傅里叶变换,结果如图10所示。由图可知,这2类模型在低频段重合较好,但采用弹簧单元计算得到的高频分量幅值较EHD单元要低,故对于轴承动力学的求解,使用EHD模型可以提高振动响应的求解精度。
4. 结 论
本文以轴承磨损试验台为研究对象,基于子结构法建立了多体系统动力学模型,然后采用仿真计算与试验相结合的方法研究了滑动轴承摩擦学与动力学的耦合关系,主要得到如下结论:
1) 采用子结构法建立的轴承磨损试验台多体系统动力学模型,通过对动力学和摩擦学分别进行的试验验证,证实了建模方法的正确性。
2) 在试验工况下,轴承磨损试验台的4个支撑轴承处于完全液动润滑状态,被测轴承处于混合润滑状态,这种恶劣的润滑条件主要是因上止点的载荷较高且受力集中所致。
3) 随着间隙的增大,被测轴承的润滑状态先改善并在20 μm间隙时达到最佳,随后恶化;随着间隙的增大,最大压力随之增大,最小油膜厚度先增加后减小,摩擦功耗则是先减小后增大,因此在进行轴瓦设计时,需确定合适的间隙以同时满足润滑性能需求。
4) 当间隙较小时,采用非线性弹簧可以得到较高精度的轴承载荷,但当轴承间隙较大时,在外载的作用下轴颈与轴瓦之间存在冲击,采用EHD模型的求解精度更高。
-
表 1 轴承磨损试验台主要参数
Table 1 Main parameters of bearing wear test bed
参数 数值 参数 数值 轴承宽度b/mm 29 油孔位置/(°) 45 轴颈直径/mm 52.68 油孔直径/mm 4 径向(半径)间隙c/μm 250 进油温度/℃ 55 支撑轴瓦1(半径)间隙c1/μm 50 进油压力/bar 9 支撑轴瓦2(半径)间隙c2/μm 50 轴颈表面粗糙度/μm 0.4 润滑油牌号 10W-30 轴瓦表面粗糙度/μm 0.5 表 2 主要零部件有限元模型与缩减模型
Table 2 Finite element model and condensed model of main parts
零部件 有限元模型 缩减模型 偏心轴 

支撑轴承座 

连杆 

表 3 偏心轴有限元模型与缩减模型模态对比
Table 3 Comparison of modal frequency between finite element models and condensed model of eccentric shaft
阶数 频率/Hz 误差/% 振型 有限元模型 缩减模型 1 1 708.5 1 710.5 0.117 YZ 面内弯曲模态 2 1 718.7 1 721.7 0.175 XZ 面内弯曲模态 3 4 021.6 4 020.4 −0.030 扭转模态 4 4 332.6 4 344.5 0.275 YZ 面内弯曲模态 5 4 360.8 4 362.9 0.048 XZ 面内弯曲模态 表 4 连杆有限元模型与缩减模型模态对比
Table 4 Comparison of modal frequency between finite element model and condensed model of connecting rod
阶数 频率/Hz 误差/% 振型 有限元模型 缩减模型 1 963.5 963.23 −0.03 XZ 面内弯曲模态 2 1 213.6 1 212.4 −0.10 扭转模态 3 1 558.6 1 554.6 −0.26 YZ 面内弯曲模态 4 1 816.4 1 814.4 −0.11 小端局部模态 5 2 644.1 2 645.1 0.038 扭转模态 表 5 轴承磨损试验台主要测试参数
Table 5 Main test parameters of bearing wear test bed
传感器 信号类型 被测对象 位移传感器 位移 轴心轨迹 扭矩仪 扭矩 摩擦功耗 温度传感器 温度 瓦背温度 压力传感器 压力 供油压力 表 6 各轴承EHD润滑计算结果
Table 6 EHD calculation results of diffrent bearings of the test bed
轴承号 性能参数 pmax /MPa hmin /μm λ γ/% Wm /W 1 2.87 20.87 32.61 0 241.74 2 16.51 8.07 12.61 0 318.92 3 106.78 1.38 2.03 1.42 486.89 4 16.49 8.07 12.61 0 319.03 5 2.68 20.89 32.64 0 248.67 -
[1] 李正民, 何琳, 徐伟, 等. 轴承润滑特性对船舶推进轴系校中的影响[J]. 中国舰船研究, 2016, 11(6): 104–111. doi: 10.3969/j.issn.1673-3185.2016.06.016 LI Z M, HE L, XU W, et al. The influence of bearing lubrication characteristics on marine propulsion shaft alignment[J]. Chinese Journal of Ship Research, 2016, 11(6): 104–111 (in Chinese). doi: 10.3969/j.issn.1673-3185.2016.06.016
[2] 孙谦, 刘文玺, 周其斗. 推力轴承基座结构形式对潜艇振动噪声的影响[J]. 中国舰船研究, 2018, 13(5): 39–45. doi: 10.19693/j.issn.1673-3185.01099 SUN Q, LIU W X, ZHOU Q D. Influence of thrust bearing seating on acoustic radiation of submarine[J]. Chinese Journal of Ship Research, 2018, 13(5): 39–45 (in Chinese). doi: 10.19693/j.issn.1673-3185.01099
[3] WANG D E, KEITH T G, YANG Q M, et al. Lubrication analysis of a connecting-rod bearing in a high-speed engine. Part II: lubrication performance evaluation for non-circular bearings[J]. Tribology Transactions, 2004, 47(2): 290–298. doi: 10.1080/05698190490439436
[4] WANG D E, KEITH T G, YANG Q M, et al. Lubrication analysis of a connecting-rod bearing in a high-speed engine. Part I: rod and bearing deformation[J]. Tribology Transactions, 2004, 47(2): 280–289. doi: 10.1080/05698190490439346
[5] CRAIG JR R R, BAMPTON M C C. Coupling of substructures for dynamic analyses[J]. AIAA Journal, 1968, 6(7): 1313–1319. doi: 10.2514/3.4741
[6] CRAIG JR R R, CHANG C J. Free-interface methods of substructure coupling for dynamic analysis[J]. American Institute of Aeronautics and Astronautics, 1976, 14(11): 1633–1635. doi: 10.2514/3.7264
[7] 杜大华, 贺尔铭, 李锋. 基于多重动态子结构法的大型复杂结构动力分析技术[J]. 推进技术, 2018, 39(8): 1849–1855. DU D H, HE E M, LI F. Dynamics analysis technology of large-scale complex structures based on multilevel dynamic substructure method[J]. Journal of Propulsion Technology, 2018, 39(8): 1849–1855 (in Chinese).
[8] 李红. 碰摩转子系统动力学特性及其故障分析研究[D]. 北京: 华北电力大学, 2016. LI H. Research on dynamic characteristics and fault analysis of rubbing rotor system[D]. Beijing: North China Electric Power University, 2016 (in Chinese).
[9] GREENWOOD J A, TRIPP J H. The contact of two nominally flat rough surfaces[J]. Proceedings of the Institution of Mechanical Engineers, 1970, 185(1): 625–633. doi: 10.1243/PIME_PROC_1970_185_069_02
[10] PATIR N, CHENG H S. Application of average flow model to lubrication between rough sliding surfaces[J]. Journal of Lubrication Technology, 1979, 101(2): 220–229. doi: 10.1115/1.3453329
[11] BUKOVNIK S, DÖRR N, ČAIKA V, et al. Analysis of diverse simulation models for combustion engine journal bearings and the influence of oil condition[J]. Tribology International, 2006, 39(8): 820–826. doi: 10.1016/j.triboint.2005.07.023
[12] 卢伯聪, 向建华, 庄林毅. 基于动态子结构的主轴承热弹性流体润滑研究[J]. 润滑与密封, 2012, 37(1): 22–28. doi: 10.3969/j.issn.0254-0150.2012.01.006 LU B C, XIANG J H, ZHUANG L Y. Thermo-elastohydrodynamic lubrication research on engine main bearings based on the dynamic substructure theory[J]. Lubrication Engineering, 2012, 37(1): 22–28 (in Chinese). doi: 10.3969/j.issn.0254-0150.2012.01.006
[13] ALLMAIER H, PRIESTNER C, REICH F M, et al. Predicting friction reliably and accurately in journal bearings–the importance of extensive oil-models[J]. Tribology International, 2012, 48: 93–101. doi: 10.1016/j.triboint.2011.11.009
-
期刊类型引用(1)
1. 王小伟,唐渊,尹宁,翟贺,吴涛. FZB3G弹性金属塑料轴承材料的摩擦磨损特性分析. 金属功能材料. 2024(03): 92-98 .  百度学术
百度学术
其他类型引用(1)



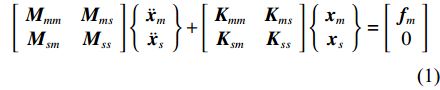
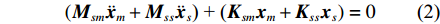
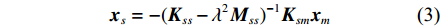
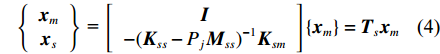
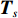
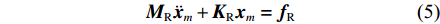
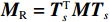
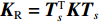
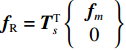
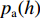
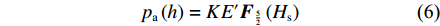
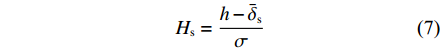
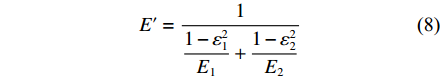
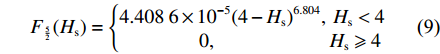
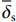
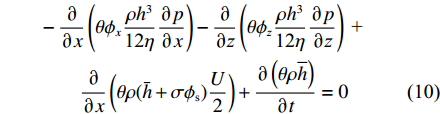
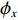
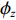
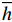
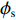

 下载:
下载:










