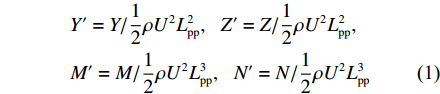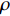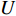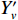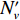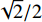Comparison of hydrodynamic characteristics of SUBOFF with cruciform and X-form rudder arrangement
-
摘要:目的 对于水下航行体的艉布局而言，相较十字形艉布局，X形艉布局具有不超宽、降低舵卡严重后果等优点。由于X形艉布局及其操纵较为特殊，其水动力特性与十字形不同。以SUBOFF为原型，通过数值计算对比十字形和X形艉布局航行体的操纵性水动力特性。方法 首先，对比十字形艉布局线性水动力的数值计算与模型试验数据，确定数值计算的网格参数；其次，对全动舵面积相同的X形艉布局航行体线性水动力进行预报，并与十字形艉布局进行对比；最后，采用体积力模拟螺旋桨抽吸，对比研究两方案操纵性水动力特性的差异。结果 结果表明：在相同全动舵面积下，相较十字形艉，X形艉布局航行体水平面静不稳定系数略小，垂直面静不稳定系数略大；受相邻两舵干扰影响，X形航行体垂直面、水平面舵力特性具有较为明显的不对称性，舵导数减小约27%；抽吸显著改变了十字形和X形艉布局航行体的水动力，舵导数增大约15%~18%。结论 研究成果可为水下航行体操纵性设计提供一定的借鉴。Abstract:Objectives Underwater vehicles with an X-plane arrangement can be designed to handle plane control jams, and are characterized by their safety over vehicles with a cruciform arrangement. Because of the different arrangement and control mode of the X-plane arrangement, its hydrodynamic characteristics are different from those of a cruciform arrangement.Methods Numerical simulations of the cruciform arrangement are carried out on SUBOFF and validated first with the model test results and then in combination with the determined meshing method. The hydrodynamic characteristics of the X-plane arrangement are then studied and compared with those of a cruciform arrangement with the same rudder area. Finally, simulations of both the cruciform and X-plane arrangements with propellers modelled by body force are carried out.Results The results show that the horizontal and vertical stability coefficient of the X-plane arrangement is almost the same and declines compared with those of the cruciform arrangement respectively. The force characteristics of the X-plane arrangement are nonlinear with its angle, and the derivatives of the rudder decline by about 27%. The pump effect improves the stability coefficients and enhances the derivatives of the control surface by about 15%–18%.Conclusions The results of this study can provide guiding references for the design of underwater vehicles.
-
0. 引 言
操纵性是水下航行体综合航行性能的重要方面，而艉操纵面的布局选型与设计直接决定了操纵性的优劣。相较十字形艉布局，X形艉布局有一定的优势。由于X形艉布局及其操纵的特殊性，其水动力特性与十字形相比有所不同。因此，对比研究2个不同艉布局的操纵性及水动力特性对于水下航行体操纵性设计及其操纵性能评估具有重要意义。
加拿大DRDC的Mackay[1]整理了1987~1988年间完成的十字形和X形艉布局潜艇缩比尾段水平面风洞模型试验结果，包括对尾段位置力和单独艉操纵面的压力测量，风洞模型试验表明：水平面内X形艉布局设计方案失速角增大，四舵同操的舵力提高。意大利CNR的Broglia等[2]针对十字形和X形艉布局潜艇深水及近水面时水平面内非定常PMM运动的水动力进行了数值模拟，并对这2个方案的稳定性进行了对比评估，研究表明，由于X形艉布局设计方案横向投影面积大于十字形艉布局，故X形艉布局方案更稳定。Zaghi等[3]采用数值模拟对上述2种布局方案在水平面内的定深回转机动进行了研究，结果表明，由于X形艉布局采用四舵同时操纵策略，其回转能力显著优于十字形艉布局方案。
针对X形舵操纵不直观的特点，张涛和林俊兴[4]通过理论分析，分别给出了X形舵相同舵面积、不同舵面积时与十字形舵的等效关系；胡坤等[5-6]在世界各国X形舵潜艇发展概况的基础上，分析了X形舵潜艇操纵性水动力（矩）和控制方法，提出了X形舵与十字形舵等效舵角转换装置设计思想，并采用数值仿真，比较了X形舵和十字形舵的操纵特性，提出了今后工作中待解决的4个问题，其中有3个是关于X形艉布局潜艇水动力特性的研究。吴军[7]基于理论计算，比较了十字形及X形艉布局的操纵特性，但这2套研究方案的艉操纵面面积不同。张露等[8]采用数值计算方法，比较了面积相等的十字形与X形艉布局水下航行体的水动力特性，包括直航阻力与不同攻角状态的升力，但未就漂角，尤其是舵角（方向舵、升降舵）相关的水动力特性对比展开进一步的研究。
综上，国内外学者已针对十字形及X形艉布局的航行体水动力特性开展了对比研究，表明了X形艉布局方案具有优良的操纵性。但是，现有研究中十字形及X形艉布局方案的设计面积往往是不同的，在研究内容上也仅局限于水平面或垂直面单一平面，且X形艉布局方案的操控均是以四舵同操模式给出。
鉴于此，以SUBOFF为原型，针对全动舵面积相同的十字形及X形艉布局，对比分析2种方案操纵性水动力特性的差异，包括攻角、漂角及舵角（升降舵、方向舵）相关的水动力特性。
1. 研究对象
本文仿真计算的对象有2个：SUBOFF原型（十字形艉布局）及SUBOFF改型（X形艉布局），如图1所示。其中，SUBOFF原型由主体、围壳、艉操纵面（4个全动舵，十字形）及呈X布置的支柱支撑的导管构成，主要参数如表1所示[9]；SUBOFF改型由原型方案艉操纵面（4个全动舵）顺时针旋转45°得到。
表 1 SUBOFF原型主要参数Table 1. Main parameters of SUBOFF prototype参数 量值 垂线间长Lpp/m 4.261 坐标原点距艏纵向距离x/m 2.013 坐标原点距基线垂线距离z/m 0.254 舵轴距舵尾缘纵向距离xR/m 0.137 舵面积S/m2 0.025 2. 计算方法验证
2.1 计算工况
文献[9]详尽给出了SUBOFF原型水平面变漂角、垂直面变攻角等相关的线性水动力（矩）导数获取方法及量值，是历来世界各国学者数值计算方法验证的重要参考。类似地，这些导数将用于本文基于STAR-CCM+建立的操纵性水动力数值计算方法的校核。该计算软件在预报分析水动力和流场方面显示了其适用性[10]。
本文数值计算方法验证的工况及其对应的导数如表2所示。计算方案中的漂角β、攻角α及侧向力Y、垂向力Z、纵倾力矩M、偏航力矩N按照通用艇体坐标系定义[9]。
表 2 计算工况Table 2. Computational cases计算工况 参量变化范围 拟合导数 变漂角 β = ±1°，±2° Yv'，Nv' 变攻角 α = ±1°，±2° Zw'，Mw' 2.2 计算参数及数据表达
参考模型试验雷诺数（Re=1.4×107）并基于平板假定，初步确定计算模型边界层最大厚度[11]；根据水下航行体操纵性水动力计算经验[12]，取y+=60，结合试验雷诺数，确定计算模型近壁面第1层网格尺寸。此外，结合操纵性水动力计算需要，针对SUBOFF原型的围壳、舵、导管及其支柱等进行了独立设置，如表3所示。
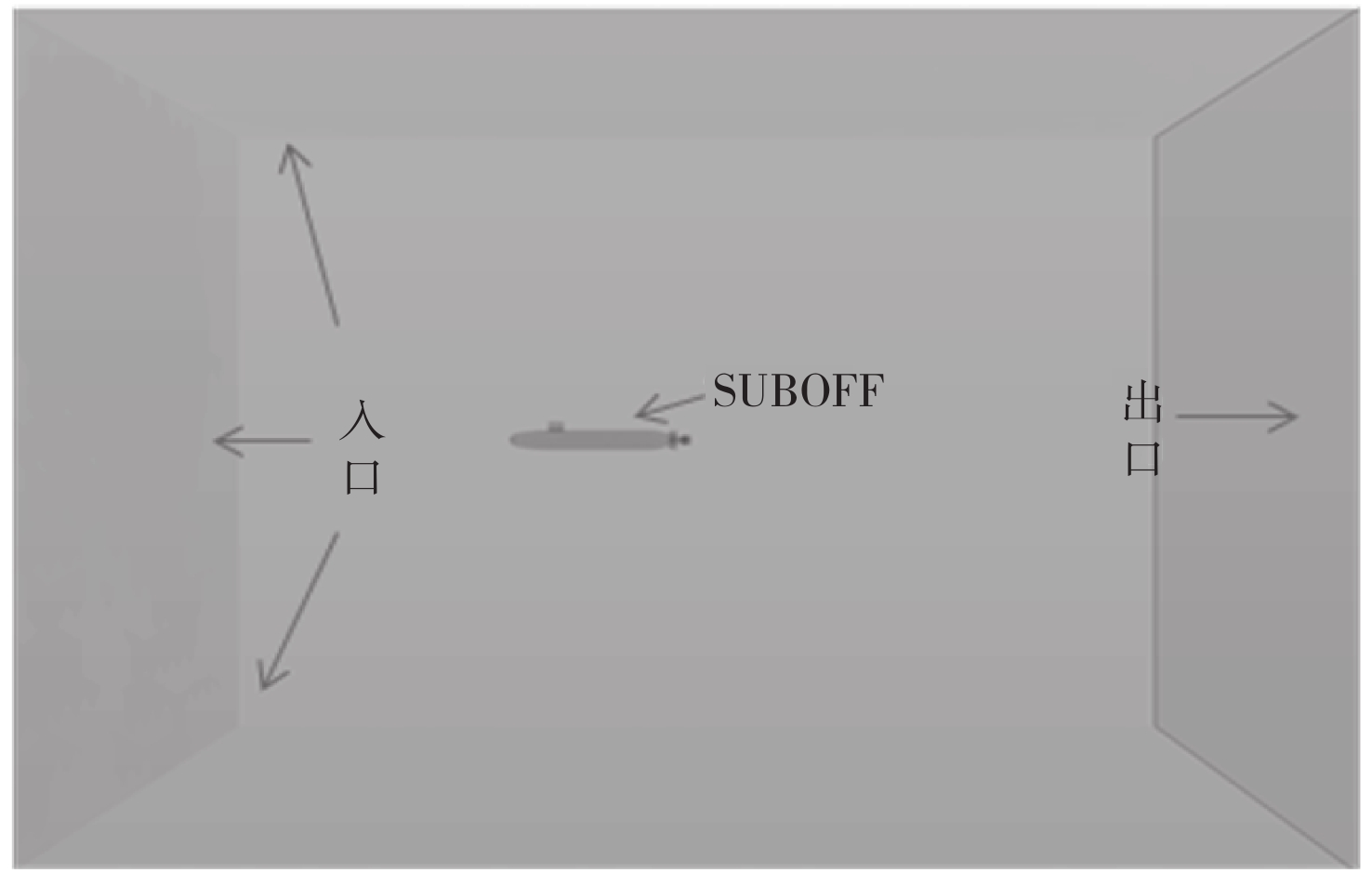
表 3 网格生成参数Table 3. Main parameters of mesh generation控制类型 参数名称 量 值 网格1 网格2 网格3 默认控制 基础尺寸/m 0.4 0.2 0.1 表面增长率 1.3 1.3 1.3 棱柱层数 10 10 10 近壁面厚度/m 0.001 0.001 0.001 棱柱层总厚度/m 0.063 0.063 0.063 自定义控制（围壳、舵、导管及支柱） 目标表面尺寸/m 0.004 0.008 0.016 最小表面尺寸/m 0.001 0.002 0.004 模型计算域为长方形，前方和侧面均取2倍艇长，后方取3倍艇长（图2）。边界条件定义如下：
1） 入口−模型前方和侧面，定义为速度入口，根据模型试验雷诺数及数值计算软件中默认的动力粘度，设定入口合速度为2.93 m/s，湍流强度取2%，湍流粘度比取2；
2） 出口−模型后方，定义为压力出口，湍流强度及粘度比与入口定义相同；
3） 物面−定义为静止无滑移。
整个计算域采用棱柱六面体网格划分。通过调整基础尺寸进行网格收敛性研究，形成了3套计算网格，如图3所示，网格数分别约40万、145万和453万。图3给出了3套不同网格中SUBOFF原型表面的网格划分。
控制方程包括时均的连续方程及N-S方程，并采用湍流模型RNG k-ε封闭。
针对SUBOFF原型，对采用数值计算方法得到的操纵性水动力进行无因次化：
Y′=Y/12ρU2L2pp,Z′=Z/12ρU2L2pp,M′=M/12ρU2L3pp,N′=N/12ρU2L3pp (1) 式中：
ρ 为流体介质密度，取997.561 kg/m3；U 为入口合速度。2.3 计算结果及验证
基于上述3套网格，开展水平面变漂角、垂直面变攻角水动力数值计算。各工况下的数值计算结果对比如图4所示，对其进行拟合得到的水动力导数如表4所示。
表 4 水动力导数对比Table 4. Comparison of hydrodynamic derivatives between different meshes水动力导数 数值计算 模型试验 偏差/%（数值计算/模型试验–1） 网格1 网格2 网格3 网格1 网格2 网格3 1 000Y′v −30.094 −28.536 −28.215 −27.834 8.1 2.5 1.4 1 000N′v −13.992 −14.058 −14.048 −13.648 2.5 3.0 2.9 1 000Zw' −16.021 −14.231 −13.934 −13.910 15.2 2.3 0.2 1 000Mw' 10.331 10.513 10.605 10.324 0.1 1.8 2.7 由表4可知，数值计算获得的漂角、攻角相关的位置力导数除Mw'外，随着网格数的增多，与模型试验的偏差越来越小，且网格2与网格3的结果基本相当，也即可以认为此时数值计算结果与网格基本无关。综合考虑计算成本及精度，本文后续研究均采用网格2对应生成的参数进行各工况的数值计算。
3. 艉操纵面布局影响
3.1 计算结果
基于前述建立的数值计算方法，针对SUBOFF原型和改型开展了艉布局改变对操纵性水动力特性影响的数值计算研究：
1） 为了比较两艉布局方案的位置力特性，针对SUBOFF改型漂角、攻角相关的操纵性水动力进行了数值计算，并处理获得了各线性位置力导数。
2）为了比较两艉布局方案的舵力特性，针对SUBOFF原型和改型舵角相关的操纵性水动力进行了数值计算（方向舵角δr、升降舵角δs=−15°~+15°、变化间隔Δ=5°），并处理获得了各个舵导数。为便于客观分析各平面内的舵导数，参考十字形艉布局左/右、上/下两舵同步操纵的特点，改型方案选取右舷两舵和下侧两舵同步操纵，分别实现十字形艉布局方向舵和升降舵的功能。图5所示为改型方案方向舵角和艉升降舵角正、负角度定义：方向舵以右舷两舵同操产生朝右舷的合力为正，反之为负；艉升降舵角以下侧两舵同操产生朝上的合力为正，反之为负。
3） 为了比较两艉布局方案带动力下的操纵性水动力特性，采用体积力模拟螺旋桨抽吸，针对SUBOFF原型和改型，对漂角、攻角和舵角相关的操纵性水动力特性进行了数值计算。这里，螺旋桨水动力特性模型采用软件默认的五叶桨模型[13]，正式计算前，根据SUBOFF原型直航阻力、螺旋桨推力间的平衡匹配，确定体积力模型的主要参数，如表5所示。
表 5 螺旋桨体积力模型主要参数设置Table 5. Main parameters setup for body force model of propeller参数 数值 内半径/m 0.04 外半径/m 0.10 厚度/m 0.03 转速/(r·min−1) 1 548 上述各工况的计算曲线及对应导数处理结果分别如图6和表6所示。其中，l′β，l′α分别为无因次水平面、垂直面水动力倾覆力臂；l′δr，l′δs分别为无因次方向舵、艉升降舵舵力臂。
![]()
图 6 计算结果对比Figure 6. Comparison of computational results between SUBOFF prototype and its modification表 6 SUBOFF原型和改型水动力导数对比Table 6. Comparison of hydrodynamic derivatives between SUBOFF prototype and its modification序号 水动力系数 无动力 有动力 原型 改型 偏差/%（改型/
原型–1）原型 改型 偏差/%（改型/
原型–1）1 1 000Yv' −28.536 −28.730 0.7 −30.155 −30.573 1.4 2 1 000Nv' −14.058 −14.034 −0.2 −13.394 −13.261 −1.0 l′β 0.493 0.488 — 0.446 0.434 — 3 1 000Zw' −14.231 −14.199 −0.2 −16.779 −16.556 −1.3 4 1 000Mw' 10.513 10.611 0.9 9.525 9.609 0.9 l′α 0.739 0.749 — 0.568 0.580 — 5 1 000Y′δr 4.885 3.517 −28.0 5.665 4.127 −27.1 6 1 000N′δr −1.945 −1.420 −27.0 −2.261 −1.641 −27.4 l′δr −0.398 −0.404 — −0.399 −0.398 — 7 1 000Z′δs −4.972 −3.566 −28.3 −5.889 −4.123 −30.0 8 1 000M′δs −1.956 −1.441 −26.3 −2.353 −1.643 −30.2 l′δs −0.393 −0.404 — 0.400 0.398 — 3.2 数据分析
由图6及表6可知，在相同全动舵面积下，不同艉布局方案的位置导数基本相当，但舵导数相差较大。具体为：
1） 相较原型，虽然改型方案艉舵在水平面、垂直面的侧投影面积减小了，但改型方案漂角相关位置导数
Y′v 略大，N′v 略小，水平面静不稳定系数略小；攻角相关位置导数Zw'略小，Mw'略大，垂直面静不稳定系数略大。2个平面内静不稳定系数差别的原因与艉舵/围壳相互干扰是关联的，表7为2个模型主、附体水平面内水动力的贡献对比，图7为漂角为2°时2个模型围壳的流线对比。由表7和图7可知：原型方案中，上舵处于围壳尾流中，水动力贡献较小，约为下舵的16%；改型方案中，X形艉布局使得围壳尾流对上舵的影响较小，水动力约为下两舵的23%，从而使得改型方案上、下四舵的贡献增大，静不稳定性系数减小。表 7 主、附体水平面水动力贡献对比Table 7. Comparison of horizontal hydrodynamic derivatives between different parts水动力导数 原 型 改 型 主体等 上舵 下舵 主体等 右上舵 左下舵 右下舵 左上舵 1 000Y′v −26.490 −0.281 −1.765 −26.412 −0.219 −0.939 −0.939 −0.219 1 000N′v −14.981 0.180 0.743 −15.035 0.093 0.408 0.408 0.093 注：原型中的“主体等”包含主体、围壳、升降舵和导管贡献；改型中的“主体等”包含主体、围壳和导管贡献。 ![]()
图 7 漂角为2°的流线图对比（左为原型；右为改型）Figure 7. Comparison of streamlines at drift angle +2° (left one is prototype configuration; right one is modified configuration)2） 相较原型，改型方案的舵导数减小了约27%，这与其艉布局是相关的：因改型方案艉舵呈X形布置，各舵产生的水动力合力在水平面、垂直面分解后约为十字形的
√2/2 倍；改型方案舵力随正、负舵角的线性度不同，表8所示为各舵正负舵角范围内分别拟合的水动力导数对比。表 8 正负舵角导数对比Table 8. Comparison of derivatives between positive and negative stern plane angles拟合范围 1000Y′δr 1000N′δr 1000Z′δs 1000M′δs −15°~0° 3.068 −1.236 −4.125 −1.694 0~+15° 4.231 −1.700 −3.129 −1.225 偏差/%（大值/小值−1） 37.9 37.6 31.8 38.3 由表8可知，改型方案正方向舵舵角时的舵导数明显大于负方向舵舵角时的情形，负升降舵舵角时的舵导数明显大于正升降舵舵角时的情形，两者的高舵导数均对应于舵艉部彼此分离情形（图5）。以升降舵为例，给出了±15°升降舵角时左下舵压力面和吸力面的压力云图对比，如图8所示。由图可见，±15°舵角对应的压力面表面云图差别不大，但在吸力面，−15°舵角时的低压极值、区域及梯度显著增加，使得负舵角下的舵导数明显增大。
![]()
图 8 改型方案升降舵表面压力云图对比（±15°）Figure 8. Comparison of pressure contours of stern plane surface for modified configuration (±15°)3） 有动力两方案对比与无动力两方案对比的结论基本一致，即两方案的位置导数相当；相较原型方案，改型方案舵导数减小达27%以上。
4） 抽吸影响。参考表6，表9给出了抽吸对两方案水动力导数的影响。由结果可见，螺旋桨抽吸使得位置力导数增大，矩导数减小；螺旋桨抽吸使得舵导数增大了约15%~18%。总体而言，抽吸对两方案垂直面的影响较为显著。
表 9 抽吸对原型及改型方案水动力导数的影响Table 9. Pump effect on hydrodynamic derivatives of SUBOFF prototype and its modification水动力导数变化量 原型 改型 1000ΔY′v −1.619 −1.843 1000ΔN′v 0.664 0.773 1000Z′w −2.548 −2.357 1000M′w −0.988 −1.002 1000ΔY′δr 0.780 0.610 1000ΔN′δr −0.316 −0.221 1000ΔZ′δs −0.917 −0.557 1000ΔM′δs −0.397 −0.202 4. 结 语
以SUBOFF为原型，针对舵面积相同的十字形及X形艉布局，较为系统地开展了有、无动力作用下攻角、漂角及舵角（升降舵、方向舵）相关的操纵性水动力特性研究，对比分析了不同艉布局方案的操纵性水动力特性差异。主要研究结论如下：
1） 相较十字形艉布局，X形航行体水平面静不稳定系数略小，垂直面静不稳定系数略大；
2） 相较十字形艉布局，X形航行体操纵同侧两舵后的舵导数减小了约27%；区别于十字形艉布局，受相邻两舵干扰的影响，X形航行体垂直面、水平面的舵力特性随正、负舵角呈现出不同的线性度；
3） 计及螺旋桨抽吸后的两方案操纵性水动力特性对比与无动力时的结论一致；
4） 螺旋桨抽吸使得位置力导数增大，矩导数减小；抽吸使得舵导数增大了约15%~18%；总体而言，抽吸对两方案垂直面的影响较为显著。
-
![]()
图 6 计算结果对比
Figure 6. Comparison of computational results between SUBOFF prototype and its modification
![]()
图 7 漂角为2°的流线图对比（左为原型；右为改型）
Figure 7. Comparison of streamlines at drift angle +2° (left one is prototype configuration; right one is modified configuration)
![]()
图 8 改型方案升降舵表面压力云图对比（±15°）
Figure 8. Comparison of pressure contours of stern plane surface for modified configuration (±15°)
表 1 SUBOFF原型主要参数
Table 1 Main parameters of SUBOFF prototype
参数 量值 垂线间长Lpp/m 4.261 坐标原点距艏纵向距离x/m 2.013 坐标原点距基线垂线距离z/m 0.254 舵轴距舵尾缘纵向距离xR/m 0.137 舵面积S/m2 0.025 
下载: 导出CSV
表 2 计算工况
Table 2 Computational cases
计算工况 参量变化范围 拟合导数 变漂角 β = ±1°，±2° Yv'，Nv' 变攻角 α = ±1°，±2° Zw'，Mw'
下载: 导出CSV
表 3 网格生成参数
Table 3 Main parameters of mesh generation
控制类型 参数名称 量 值 网格1 网格2 网格3 默认控制 基础尺寸/m 0.4 0.2 0.1 表面增长率 1.3 1.3 1.3 棱柱层数 10 10 10 近壁面厚度/m 0.001 0.001 0.001 棱柱层总厚度/m 0.063 0.063 0.063 自定义控制（围壳、舵、导管及支柱） 目标表面尺寸/m 0.004 0.008 0.016 最小表面尺寸/m 0.001 0.002 0.004
下载: 导出CSV
表 4 水动力导数对比
Table 4 Comparison of hydrodynamic derivatives between different meshes
水动力导数 数值计算 模型试验 偏差/%（数值计算/模型试验–1） 网格1 网格2 网格3 网格1 网格2 网格3 1 000Y′v −30.094 −28.536 −28.215 −27.834 8.1 2.5 1.4 1 000N′v −13.992 −14.058 −14.048 −13.648 2.5 3.0 2.9 1 000Zw' −16.021 −14.231 −13.934 −13.910 15.2 2.3 0.2 1 000Mw' 10.331 10.513 10.605 10.324 0.1 1.8 2.7
下载: 导出CSV
表 5 螺旋桨体积力模型主要参数设置
Table 5 Main parameters setup for body force model of propeller
参数 数值 内半径/m 0.04 外半径/m 0.10 厚度/m 0.03 转速/(r·min−1) 1 548
下载: 导出CSV
表 6 SUBOFF原型和改型水动力导数对比
Table 6 Comparison of hydrodynamic derivatives between SUBOFF prototype and its modification
序号 水动力系数 无动力 有动力 原型 改型 偏差/%（改型/
原型–1）原型 改型 偏差/%（改型/
原型–1）1 1 000Yv' −28.536 −28.730 0.7 −30.155 −30.573 1.4 2 1 000Nv' −14.058 −14.034 −0.2 −13.394 −13.261 −1.0 l′β 0.493 0.488 — 0.446 0.434 — 3 1 000Zw' −14.231 −14.199 −0.2 −16.779 −16.556 −1.3 4 1 000Mw' 10.513 10.611 0.9 9.525 9.609 0.9 l′α 0.739 0.749 — 0.568 0.580 — 5 1 000Y′δr 4.885 3.517 −28.0 5.665 4.127 −27.1 6 1 000N′δr −1.945 −1.420 −27.0 −2.261 −1.641 −27.4 l′δr −0.398 −0.404 — −0.399 −0.398 — 7 1 000Z′δs −4.972 −3.566 −28.3 −5.889 −4.123 −30.0 8 1 000M′δs −1.956 −1.441 −26.3 −2.353 −1.643 −30.2 l′δs −0.393 −0.404 — 0.400 0.398 —
下载: 导出CSV
表 7 主、附体水平面水动力贡献对比
Table 7 Comparison of horizontal hydrodynamic derivatives between different parts
水动力导数 原 型 改 型 主体等 上舵 下舵 主体等 右上舵 左下舵 右下舵 左上舵 1 000Y′v −26.490 −0.281 −1.765 −26.412 −0.219 −0.939 −0.939 −0.219 1 000N′v −14.981 0.180 0.743 −15.035 0.093 0.408 0.408 0.093 注：原型中的“主体等”包含主体、围壳、升降舵和导管贡献；改型中的“主体等”包含主体、围壳和导管贡献。
下载: 导出CSV
表 8 正负舵角导数对比
Table 8 Comparison of derivatives between positive and negative stern plane angles
拟合范围 1000Y′δr 1000N′δr 1000Z′δs 1000M′δs −15°~0° 3.068 −1.236 −4.125 −1.694 0~+15° 4.231 −1.700 −3.129 −1.225 偏差/%（大值/小值−1） 37.9 37.6 31.8 38.3
下载: 导出CSV
表 9 抽吸对原型及改型方案水动力导数的影响
Table 9 Pump effect on hydrodynamic derivatives of SUBOFF prototype and its modification
水动力导数变化量 原型 改型 1000ΔY′v −1.619 −1.843 1000ΔN′v 0.664 0.773 1000Z′w −2.548 −2.357 1000M′w −0.988 −1.002 1000ΔY′δr 0.780 0.610 1000ΔN′δr −0.316 −0.221 1000ΔZ′δs −0.917 −0.557 1000ΔM′δs −0.397 −0.202
下载: 导出CSV
-
[1] MACKAY M. Wind tunnel experiments with a submarine afterbody model[R]. Technical Memorandum DRDC Atlantic TM 2002-194, 2003.
[2] BROGLIA R, DUBBIOSO G, ZAGHI S, et al. Analysis of a submarine manoeuvrability by numerical PMM tests[C]//European Conference on Undersea Defence Technology (UDT2014). Liverpool, England, 2014.
[3] ZAGHI S, DUBBIOSO G, BROGLIA R, et al. Virtual PMM and free running manoeuvring predictions of a submarine by CFD[C]//NAV 2015 18th International Conference on Ships and Shipping Research. Rotterdam, Netherlands: ATENA, Polytechnic School of University of Genoa and Technical University of Milan, 2015.
[4] 张涛, 林俊兴. 潜艇X形舵和十字形舵等效舵角研究[J]. 船海工程, 2004, 26(5): 1–3. doi: 10.3963/j.issn.1671-7953.2004.05.002 ZHANG T, LIN J X. Study on the equivalent rudder angle between X type and cruciform rudders on submarine[J]. Ship & Ocean Engineering, 2004, 26(5): 1–3 (in Chinese). doi: 10.3963/j.issn.1671-7953.2004.05.002
[5] 胡坤, 徐亦凡. 舵型对潜艇操纵特性影响的仿真分析[J]. 船舶工程, 2005, 27(1): 41–45. doi: 10.3969/j.issn.1000-6982.2005.01.010 HU K, XU Y F. Simulation analysis of effect of submarine rudder type on maneuvering characteristics[J]. Ship & Ocean Engineering, 2005, 27(1): 41–45 (in Chinese). doi: 10.3969/j.issn.1000-6982.2005.01.010
[6] 胡坤, 徐亦凡, 王树宗. 潜艇X舵发展概况及其操纵控制特性分析[J]. 中国造船, 2007, 48(2): 130–136. doi: 10.3969/j.issn.1000-4882.2007.02.017 HU K, XU Y F, WANG S Z. X Rudder submarine′s development history and the analysis of it′s manipulative characteristic[J]. Shipbuilding of China, 2007, 48(2): 130–136 (in Chinese). doi: 10.3969/j.issn.1000-4882.2007.02.017
[7] 吴军. 潜艇操纵面及操艇性能设计研究[D]. 武汉: 华中科技大学, 2005. WU J. Study on the design of the control surface and its maneuverability for the submarine[D]. Wuhan: Huazhong University of Science and Technology, 2005 (in Chinese).
[8] 张露, 肖昌润, 焦玉超. 十字舵与X舵潜艇的水动力性能数值比较[J]. 舰船科学技术, 2017, 39(7): 24–28. doi: 10.3404/j.issn.1672-7649.2017.07.005 ZHANG L, XIAO C R, JIAO Y C. Numerical comparison on hydrodynamic performance of cross rudder and X rudder submarine[J]. Ship Science and Technology, 2017, 39(7): 24–28 (in Chinese). doi: 10.3404/j.issn.1672-7649.2017.07.005
[9] RODDY R F. Investigation of the stability and control characteristics of several configurations of the DARPA SUBOFF Model (DTRC Model 5470) from captive-model experiments[R]. Report DTRC/SHD-1298-08, 1990.
[10] 李士强, 肖昌润, 曹植珺. 基于STAR-CCM+的潜艇尾流场及水动力数值分析[J]. 中国舰船研究, 2018, 13(S1): 29–35. LI S Q, XIAO C R, CAO Z J. Numerical analysis of wake flow and hydrodynamics for a submarine based on STAR-CCM+[J]. Chinese Journal of Ship Research, 2018, 13(S1): 29–35 (in Chinese).
[11] 张亮, 李云波. 流体力学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2001. ZHANG L, LI Y B. Hydrodynamics[M]. Harbin: Harbin Engineering University Press, 2001 (in Chinese).
[12] 潘子英, 吴宝山, 沈泓萃. CFD在潜艇操纵性水动力工程预报中的应用研究[J]. 船舶力学, 2004, 8(5): 42–51. doi: 10.3969/j.issn.1007-7294.2004.05.006 PAN Z Y, WU B S, SHEN H C. Research of CFD application in engineering estimation of submarine maneuverability hydrodynamic forces[J]. Journal of Ship Mechanics, 2004, 8(5): 42–51 (in Chinese). doi: 10.3969/j.issn.1007-7294.2004.05.006
[13] STAR-CCM+ Version 10.02 user guide[CD]. CD-adapco, 2015.
-
期刊类型引用(8)
1. 李永成，李迎华，潘子英，张明辉. 浅水效应下智能技术试验船回转操纵性数值模拟. 舰船科学技术. 2024(03): 46-49 . 
百度学术
2. 陈莺. 基于非线性规划的X舵AUV容错控制. 水下无人系统学报. 2024(02): 345-353 . 百度学术
3. 李永成，李迎华，潘子英，张楠，张明辉，张璇. 吹吸射流装置对水下航行体操纵性能影响数值模拟研究. 中国造船. 2024(04): 113-124 . 百度学术
4. 陈纪军，潘子英，郑文涛，陈默，夏贤，肖冬林. X形艉水下航行体姿态角对舵水动力特性的影响. 中国舰船研究. 2023(01): 99-106 . 本站查看
5. 马琳，谢新连，王昊泽. 基于改进证据推理法的舰艇综合操纵性能评价方法. 中国舰船研究. 2023(03): 94-103 . 本站查看
6. 操戈，余嘉威，冯大奎，张志国，姚朝帮. 基于体积力方法的船舶波浪回转运动数值仿真. 舰船科学技术. 2022(01): 39-45 . 百度学术
7. 张天，吴家鸣，廖华，吕海燕，杨显原. H型尾操纵面模型在潜艇超越运动中的性能分析. 舰船科学技术. 2022(01): 17-22 . 百度学术
8. 陈纪军，潘子英，夏贤，郑文涛. X形艉舵水下航行体变舵角水动力特性及其数学模型研究. 船舶力学. 2022(05): 617-627 . 百度学术
其他类型引用(3)
-
其他相关附件
-
本文双语pdf
2020-2-8_en 点击下载(4057KB)
-
计量
- 文章访问数: 1232
- HTML全文浏览量: 305
- PDF下载量: 134
- 被引次数: 11
