0.   引　言

船舶设计制造是一项涉及多个工业体系，涵盖水动力学、动力学、静力学等多学科的复杂技术，是一个国家工业水平的体现。船舶设计包括船体结构设计、动力系统设计、设备配置、强度计算、舾装设计等，需要考虑材料选择、制造工艺、法规标准等^[1]。船舶概念方案设计作为船舶设计的前端环节，通过对主尺度、型线等关键参数的初步拟定，从而达到缩短整体设计周期的目的。然而，面对日益多样化、复杂化的船舶功能需求，该过程需深度融合多学科知识及专家经验，往往耗费大量人力和时间成本，背离其高效辅助决策的初衷。

随着船舶工业的发展，面对日趋多样化的船舶功能需求及随之提升的概念方案设计复杂性，研究者们正从船舶专家设计船型概念方案、计算机辅助设计船型概念方案以及利用模糊推理系统快速生成船舶概念方案几个方面寻求解决方案。

1） 不同的研究者根据自己相关领域针对不同功能需求的船舶进行独立的概念方案设计研究，例如分析无人救援船、战略石油储备船等的使用需求，分别针对其使用环境、功能特性等进行设计。

2） 为减小概念方案设计的时间成本，研究人员利用近年来愈发成熟的计算机以及数字仿真技术辅助寻找船型设计参数之间的耦合关系^[6-8]，从而缩短概念方案设计周期。尤其在针对概念方案中的多目标优化问题方面取得了诸多成果。文献[9]基于多目标优化的方案设计系统，采用并行处理方式，缩短了船舶概念方案设计的周期^[9]。文献[10]为了解决多目标问题，应用最小−最大适应度多目标粒子群优化算法，结合专家经验与信息熵权的主客观混合赋权TOPSIS法对船舶概念方案进行了快速优化。另外，文献[11]基于改进的遗传算法，将其应用于潜艇概念方案设计当中。这些方法能够针对船舶概念方案设计中不同参数之间的耦合关系，快速生成或优化相应的概念方案，并且具有不错的稳定性和可靠性。此外，在国际相关领域也有类似工作的报道。比如，Mauro等^[12]结合决策树和多元线性回归设计了一种船舶主尺度参数估计的方法，为船舶设计者在早期设计阶段提供了对主尺度参数估计的工具。Gary等^[13]结合人类设计师与模糊逻辑开发的船舶概念方案辅助设计系统，使设计师可以通过图形界面（GUI）和网络软件工具与一个计算型的模糊逻辑系统互动，帮助设计师在概念方案设计阶段进行决策。Degan等^[14]构建了一种基于数学模型（MDM）的多属性决策方法（MADM），可以快速生成通过技术检验的船舶概念方案。更多相关文章可见文献[15-17]。这些方法重点与机器学习相结合，构建概念方案辅助设计系统，主要用于辅助设计师设计船舶概念方案；通过建立船舶概念方案的数学模型，快速生成船舶概念方案。

3） 尽管上述方法能够相对快速地生成船舶的概念方案，但多数智能方法仅针对特定船型或预设场景开发，模型固化，难以适应日新月异的定制化需求。对于创新船型或特殊功能需求，模型迁移性差。而数据驱动方法依赖高质量历史数据或先验知识库，这在创新设计中尤为匮乏。同时，专家经验的深度集成仍不足，优化算法的“黑箱”特性缺乏对复杂约束冲突的透明解释^[9-12]，难以说服设计师。其他依据数学模型建立的计算机辅助概念方案生成系统则存在过于依赖设计师经验总结、存在主观偏差，且难以量化隐性知识^[13]，或存在应用场景受限、船型普适性低的问题^[14]。对此，杨萌等^[18]基于用户对船的性能需求中通常带有的模糊属性，例如“航程非常大”中的“非常大”这种模糊性的需求，基于模糊集、模糊逻辑^[19]、普适专家经验的简洁可解释模糊规则以及模糊推理开发了能够根据不同用户需求快速生成船舶概念方案的系统。该系统将用户对船舶的性能需求通过模糊推理转化为相对应的性能数值，再将推理所得的性能参数值根据母型船库转化为设计参数进行二次模糊推理，最终得到船型概念方案。该模糊推理系统不仅快速且能够应对不同类型的船舶设计需求，具有优异的准确性。但其在船型性能参数推理过程的准确性以及概念方案是否符合船型设计合理性方面，尚有一些问题没有考虑。首先，在对用户需求的船型性能参数的推理过程中，没有验证推理所得的船型性能参数值是否符合用户需求，如果推理所得的性能参数值中某一个参数很大程度地偏离了用户的需求，那么对最终的船型概念方案符合用户需求的程度有极大的影响。其次，船舶的不同设计参数之间存在耦合关系。在对整个模糊推理生成系统的合理性评估中，没有考虑不同类型的船舶之间其设计参数的耦合关系不同。将推理的船型概念方案与不同类型的船舶概念方案比较，无法作为合理性判断的依据。

因此，本研究将针对上述问题，对整个模糊推理系统进行优化，将类栈式结构^[20]嵌入到船舶性能参数的推理过程当中，结合用户需求本身的信息与推理信息，以提高推理所得性能参数符合用户需求的程度。同时，还将推理所得的概念方案与母型船库中的方案进行分类，以将同一类型的方案进行对比，从而提高船舶合理性评估的可靠性。

1.   基于类栈式结构的模糊快速推理模型

1.1   相关性工作

本小节将介绍模糊推理系统中用户需求的模糊化以及性能参数值的推理计算过程。并简要阐述由性能参数映射到船型设计参数的过程。

1.1.1   性能参数生成

根据用户提供的含模糊变量的原始输入需求，在模糊集基础上建模，将模糊化需求表示为数值向量。模糊系统中，不同程度的语言变量被映射到对应区间以构成模糊集。针对语言变量的模糊化，本研究采用五等分法^[21]将区间(0,1)划分为[0, 0.2] [0.2, 0.4] [0.4, 0.6] [0.6, 0.8] [0.8, 1]，分别对应语言解释“非常小”“小”“中”“大”“非常大”。例如，“航行里程远大于5 000 km”中，“远大于”对应第2区间“小”的隶属度为0，第4区间“大”为0.7，第5区间“非常大”为0.9（隶属度通常由专家设定）。对清晰数值（如“5 000 km”）的模糊化，则通过隶属度函数（如高斯函数）转换。高斯隶属度函数^[22]因其平滑性、对称性及与自然分布的相似性，被广泛用于模糊系统，其形式为

式中：i=1，2，3，…，d；d表示用户需求的特征数量；j=1，2，…，M，M表示划分的模糊区间数量，在本研究中$M = 5$；${c}_{i, j}$与${\sigma _{i,j}}$分别表示隶属中心与方差，为2个超参数，在本研究中采用模糊聚类方法（FCM） ^[23]，根据已有的母型船性能参数库生成。FCM的大致实现过程如下。

首先，设定聚类簇数M、模糊因子m以及迭代停止阈值等参数（本研究将在算例验证部分进行阐述），并随机初始化隶属度矩阵${U^0}$，满足$\sum\limits_{i = 1}^M {{u_{ij}} = 1}$，即每个样本隶属度和为1。

其次，计算每个簇的中心：

式中：${x_j}$为第j个样本；${u_{ij}}$表示第j个样本对簇i的隶属度。

而后，更新隶属度${u_{ij}}$直到误差低于迭代停止阈值或最大迭代轮次：

式中，${d_{ij}} = \left\| {{x_j} - {v_i}} \right\|$表示第j个样本到簇i的欧式距离。通过上述交替更新实现最小化目标函数：

记模糊化的船型性能数值为V，其隶属度矩阵表示为

式中，${\mu ^V}_{ij}$表示第i个用户需求的性能参数隶属于第j个模糊区间的隶属程度。

同样，记模糊的用户需求的语言变量为L，其隶属度矩阵表示为

式中，${\mu ^L}_{ij}$表示第i个用户需求的语言变量隶属于第j个模糊区间的隶属程度。

于是，根据2个用户需求的隶属度矩阵作为模糊推理的前提条件，进行符合用户需求的船型性能数值模糊推理。

1.1.2   模糊推理

在模糊推理的过程中，包含3个阶段，分别为模糊化、模糊推理和反模糊化。第1.1.1小节中介绍的2个关于用户需求的隶属度矩阵则对应模糊化阶段。接下来，则以2个隶属度矩阵为前件，根据特定的模糊规则进行模糊推理，从而得到符合用户需求的船型性能参数值。在本项工作中，模糊规则根据专家意见进行设定。

观察${U^V}$矩阵的第j行$\left[{\mu }_{\text{j}, 1}^{V}, {\mu }_{\text{j}, \text{2}}^{V}, \ldots , {\mu }_{\text{j,M}}^{V}\right]$，j表示第j个性能参数，此时，该行最大的元素所在的模糊区间表示该性能参数应隶属于哪个模糊区间。例如，假设该行第3个元素${\mu _{{\text{j,3}}}}^V$为该行最大的元素，则该行元素所表达的模糊含义为第j个性能参数值的模糊语义为“中”。${U^L}$同理，因此可以得到2个模糊量，最后根据模糊规则生成对应的用户需求性能参数。具体见表1。

表  1  模糊规则

Table  1.  Fuzzy rule table

F(V)	F(L)
	非常小	小	中	大	非常大
非常小	非常小	非常小	非常小	小	中
小	非常小	非常小	小	中	大
中	非常小	小	中	大	非常大
大	小	中	大	非常大	非常大
非常大	中	大	非常大	非常大	非常大

下载: 导出CSV 

| 显示表格

表中$F(L)$表示模糊语言变量，$F(V)$表示模糊性能参数数值。由此可以根据模糊规则进行模糊推理，例如：

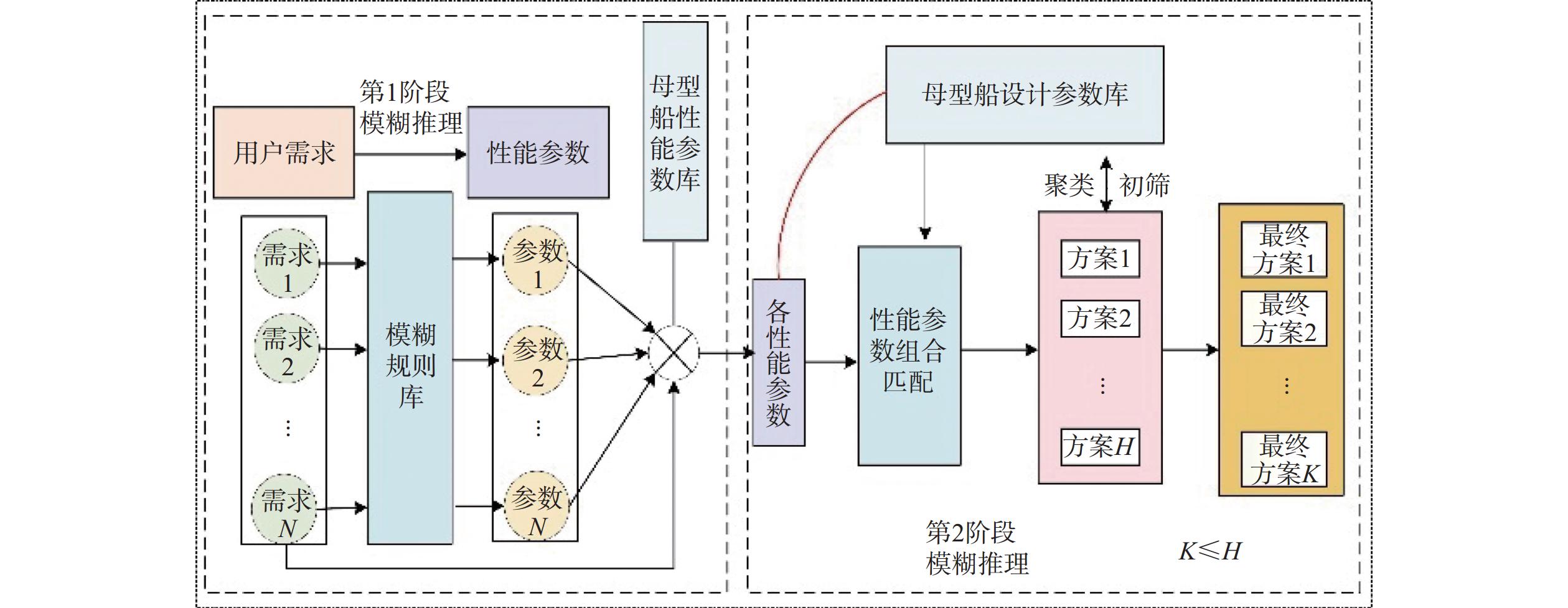
由此得到一组符合用户需求的船型性能参数值。经过反模糊化后，根据该组性能参数与母型船性能参数库通过欧式距离最小进行匹配，得到与推理所得的性能参数值最接近的母型船性能参数序号。通过该组序号匹配相对应的母型船设计参数，得到的每组设计参数值都符合对应的单个性能参数值。最后利用高斯隶属函数将所有设计参数模糊化，通过模糊推理算子“and”综合考虑符合所有性能参数值的设计参数，最终经过反模糊化得到船型概念方案。由于篇幅问题，本文仅介绍设计参数推理的总体过程，详细的推理过程可见文献[18]。

1.2   模型优化

在船型设计的二阶段模糊推理过程中，如果第1阶段的性能参数推理结果未能满足用户需求，那么第2阶段生成的设计参数可能会偏离实际要求。并且第2阶段推理仅通过简单的参数映射关系来确定设计参数，未能充分考虑不同参数之间耦合关系，导致最终的概念方案可能不符合船舶设计的合理性。

因此，本研究针对上述局限性对推理模型进行优化，主要包括以下2点。

1.2.1   性能参数模糊推理优化

针对第1阶段所推理得到的船舶性能参数值可能不契合用户需求的问题，一般的方法是设计一种评估方法对推理结果进行评估，并对不满足用户需求的性能参数值进行优化。但直接对不满足要求的性能参数进行优化极其复杂和困难。其原因是性能参数的模糊推理过程是基于专家建议的模糊规则库。如果要对性能参数进行优化，则涉及模糊规则库的优化，这会增加整个模型的复杂程度，影响模型的推理效率以及可解释性。因此，本研究试图通过一种新的角度来减小可能存在的错误推理对于模型推理准确度的影响。

由于不同阶段的概念方案推理形成的知识表示和决策结论具有一定的差异性和互补性，在某一特定阶段很难形成满足用户需求的概念方案解；此外，由于用户需求的天然不确定性，不同阶段生成的概念方案解具有模糊性。因此，本研究的创新之处在于构建一种类栈式结构，能够保证最终的性能参数值符合相应的模糊推理规则（用户不确定性需求），同时将不同阶段推理过程中的决策误差限定在可控范围内，从而提高最终性能参数值符合用户需求的程度。

该方法的实现流程如下所示。

假设第1阶段直接推理所得到一条符合要求的性能参数为

式中：$Per_j^{({\rm{infer}})}$表示第j个符合要求的性能参数值，d表示总共有d个性能参数；${\mathrm{infer}}$表示该参数是模糊推理后的参数。

则本研究所提出的方法可以表示为

式中：Z是一个$(0,0.01)$区间内的随机偏置矩阵；${{\boldsymbol{X}}_{\rm{input}}}$表示原始用户输入的性能参数值。

将偏差更小的${\boldsymbol{Per}}_{( {\rm{infer}} )}'$作为第2阶段模糊推理的输入，能够有效提高推理所得的设计参数与用户需求相符合的程度。

传统的栈式结构^[24]，由Zhou等^[20]在多层次模糊神经网络结构中的相关工作中提出，主要表现为当前层网络的输入由原始输入与前层网络的输出的偏置共同构成。该方法是处理不同层神经网络之间的关系，主要应用领域为多层次神经网络。而本研究设计的类栈式结构求解船舶概念方案则是首次在船舶概念方案设计领域的尝试，也是对多层次神经网络建模的补充。

与传统推理方法相比，本研究提出的方法在建模结构和推理求解的过程方面都具有明显的差异性和先进性。传统方法的结构仅通过推理得到的性能参数值对设计参数进行推理，而本研究既考虑了性能参数值的影响，也避免了第2阶段推理的前提条件与用户需求的偏离。

考虑到模糊算子的不确定性，也为确保最终推理得到的性能参数满足用户需求，本研究设定了一种最优性能参数值选择机制。根据每个用户输入的性能参数的语言变量和性能参数值，在初始推理得到的性能参数值与通过栈式结构变换的性能参数值中，选择其中更加贴近用户需求的作为第2阶段模糊推理的输入。选择机制为：当用户需求语言变量为“小”“大”时，默认选择本研究提出的栈式结构变换后的性能参数值；当语言变量为“非常小”时，选择其中比用户输入的性能参数值更小的性能参数值；当语言变量为“非常大”时，选择其中比用户输入的性能参数值更大的性能参数值；当语言变量为“等于”时，选择更加贴近用户输入的性能参数值。

1.2.2   设计方案合理性优化

在文献[18]的研究中，其两阶段设计参数的模糊推理过程如下：首先，利用第1阶段推理得到的每条符合要求的性能参数，匹配母型船库中的对应设计参数；随后，对映射出的所有船型方案取“and”操作；最终，推理出一条船型的设计参数。该方法能确保每个设计参数均落在所有性能参数要求的区间内。然而，实际船舶设计中，设计参数不能仅基于性能需求独立确定，因其之间存在耦合关系。上述推理过程未考虑这种耦合，导致所得概念方案可能缺乏设计合理性。

为此，本研究提出一种船型概念方案合理性优化方法，通过确保推理结果与同类母型船的一致性，减少因参数耦合失衡引发的设计缺陷。

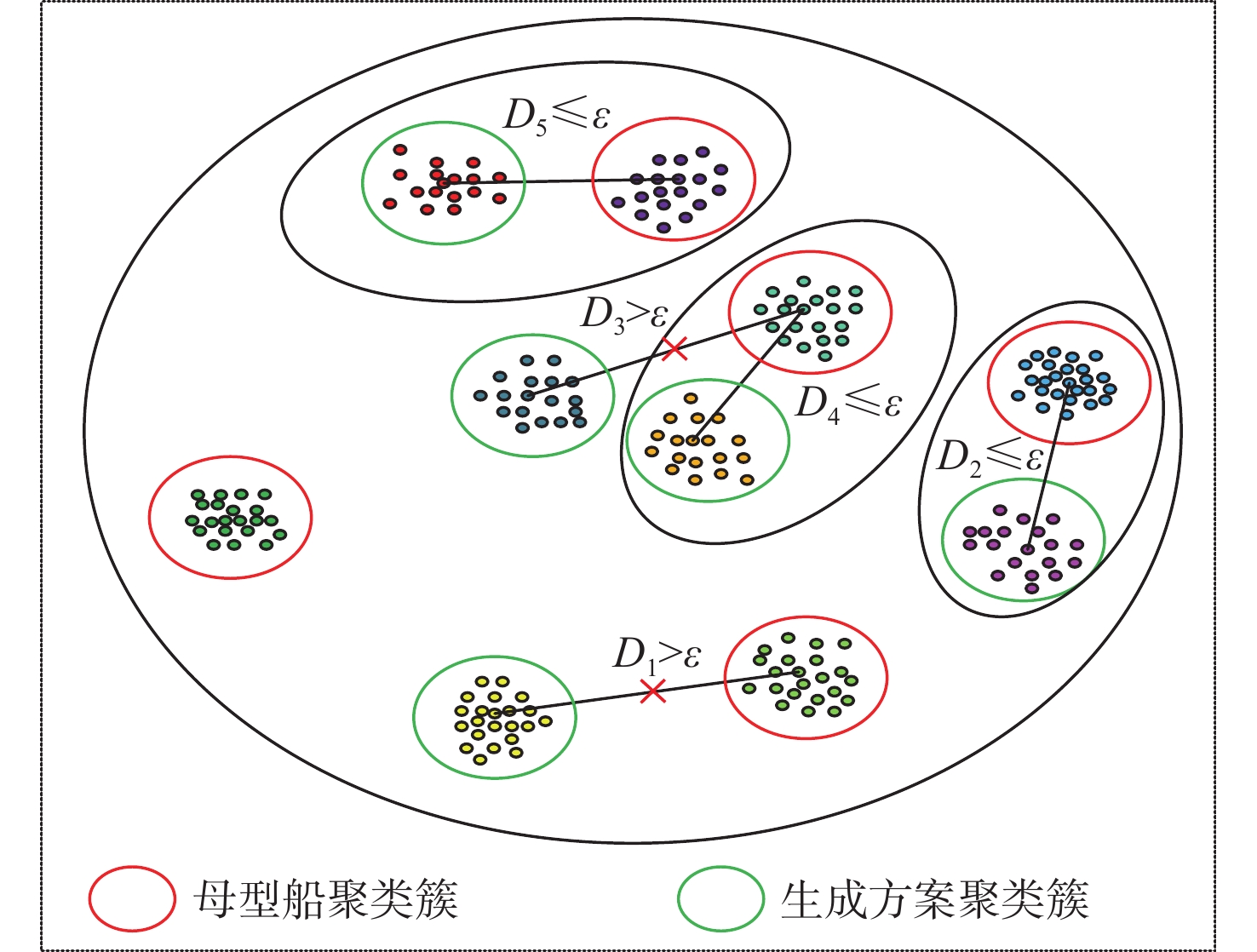
第2阶段推理生成的概念方案基于母型船参数库，其设计参数与库中母型船具有较高相似性。为提升合理性，本研究将生成方案库与母型船库按设计参数相似性分类，将生成方案与母型船整体差距更小的概念方案划分为近似类别。最后，定量评估同类生成方案与母型船的差异。因母型船方案已被验证合理，若生成方案与母型船的差异低于阈值，则认为其符合设计合理性要求。

本研究将推理所得设计方案库与母型船设计方案库中的样本利用K-means聚类方法^[25]分别各自进行聚类。

1.2.2.1   聚类初始化

在K-means++的^[26]基础上，对聚类中心初始化方法进行了优化，其过程如下。

首先，通过密度阈值对数据进行去噪，在此基础上进行归一化，并利用主成分分析降维(PCA)方法降维。然后，从数据集中随机选择一个点，其概率与局部密度成正比（局部密度为以随机选择点${c_i}$为中心，r为半径范围内的所有点）。接着对范围内的所有点，根据式（9）计算其到已选中心的最小加权距离平方：

结合距离与密度计算概率分布：

最后，总共运行N次上述初始化过程，得到N组聚类中心，并对每一组计算其轮廓系数，选择得分最高的一组作为最终初始化聚类中心。

1.2.2.2   聚类计算过程

由此将2个库中的数据分为c类，分别得到c个聚类中心。K-means聚类的计算过程如下。

首先，从分别从推理所得设计参数库与母型船设计参数库中随机初始化c个初始聚类中心：

式中：${\boldsymbol{C}}_i^S$表示推理所得船型设计方案聚类中心；${\boldsymbol{C}}_i^P$表示母型船设计参数库聚类中心。

然后，分别计算各自库中剩余数据对象与聚类中心${\boldsymbol{C}}_i^S$，${\boldsymbol{C}}_i^P$的欧氏距离${{\boldsymbol{D}}_s}$，${{\boldsymbol{D}}_P}$，判断距离每一个样本最近的聚类中心，并将该样本归类到聚类中心所对应的簇中。

最后，计算每个簇中数据对象的平均值作为新的聚类中心，进行下一次迭代，直到聚类中心不再变化或达到最大的迭代次数停止。

1.2.2.3   方案合理性优化

经过上述聚类，2个样本库中的数据分别被归类为c个类别，此时，再计算推理所得设计参数样本库中的每个聚类中心到母型船设计参数库的每个聚类中心的欧式距离${{\boldsymbol{D}}_{\rm{CC}}}$，其表现形式为

式中，${{\boldsymbol{D}}_{{\boldsymbol{C}}_i^S{\boldsymbol{C}}_i^P}}$表示推理所得设计参数库的第i个聚类中心到母型船设计参数库的第j个聚类中心的距离。

对${{\boldsymbol{D}}_{\rm{CC}}}$矩阵的每一行取最小值：

现在，计算得到了推理所得设计参数库中每个聚类中心与母型船设计参数库聚类中心距离的最小值，以此表示推理所得设计参数库中的每一类对应母型船设计参数库的类别，由此建立了2个参数库之间的类别关系。然而，仅用这种方式将2个参数库中的样本建立类别关系，有一个较为明显的缺陷，即${{\boldsymbol{D}}_{\min }}$中的距离是计算所得的最小的距离，但其实际上是一个较大的量，那么该情况下，${{\boldsymbol{D}}_{\min }}$显然无法作为将2个库中的样本归为同一类的依据，此时2个样本之间存在较大的差异。因此，还需要对推理所得的设计参数库中的样本进一步筛选。根据专家意见设定一个足够小的阈值，当每个类别的样本到所对应的母型船设计参数库中的聚类中心的距离低于该阈值时，可以认为2个样本库中的数据属于近似样本。满足该条件的样本与母型船参数库的样本具有较为接近的合理性。差异化判别公式为

式中：${\boldsymbol{D}}_{{\boldsymbol{C}}_i^P}^{\rm{infer}}$表示推理所得船型设计参数库的样本到其对应母型船参数库中的聚类中心的距离；$\varepsilon$是根据专家经验，人为设定的一个较小的值。

如图1所示，图中${{\boldsymbol{D}}_1} > \varepsilon$，${{\boldsymbol{D}}_3} > \varepsilon$，因此与之相关的2个生成方案簇被认为与母型船方案库中的同类样本差异过大，不能作为合理的设计方案。而${{\boldsymbol{D}}_2} \leqslant \varepsilon$，${{\boldsymbol{D}}_4} \leqslant \varepsilon$，${{\boldsymbol{D}}_5} \leqslant \varepsilon$表明与之相关的3个生成方案簇与母型船方案库的差异较小，可以被认为是较为合理的方案。

图  1  差异评估过程

Figure  1.  Difference evaluation process

下载: 全尺寸图片 幻灯片

本研究通过提出上述的2个方法，减小了错误推理对于最终设计方案符合用户需求程度的影响。并将推理所得的设计参数方案库中的样本与母型船设计参数库中的样本建立类别关系，并量化每个推理所得的方案与母型船库中方案之间的差异，从而保证最终的推理概念方案的设计合理性。该系统的整体过程如图2所示。

图  2  模糊推理系统流程

Figure  2.  Process of fuzzy inference system

下载: 全尺寸图片 幻灯片

此外，由于本研究所提出的船型设计合理性优化方法依赖母型船库中的船型，因此，可能会出现推理结果为空的极端情况（所有推理结果不属于母型船库中任意船型）。对此，本研究采取以下措施：采用多轮生成的性能参数作为设计参数推理的输入，尽可能地生成更多的初始概念方案解，并与母型船库进行对比，找到若干较优的方案。若多轮推理迭代后，母型船设计参数库中依旧没有用户所需船型的相似模型，可以考虑在高维空间下对多维概念方案解进行增广。具体做法是：通过模糊聚类划分子凸包空间，结合密度驱动的改进凸包插值法实现数据增广。大体实现过程为：通过FCM算法对所有初始方案解聚类，计算所有初始概念方案解隶属度，由于隶属度能够反映样本与聚类中心的距离，因此，将隶属度从大至小排列，以降幅最剧烈的位置作为一个凸包子空间的边界。

子凸包空间范围内数据点分布的密度比定义为

式中：$b = 1,2, \ldots ,{B_t}$；${B_t} \in \{ 1,2, \ldots ,N - 1\}$为子凸包空间的边界；$t = 1,2, \ldots ,T$，T为子凸包空间数量；${\hat x^t}$为密度向量。

采用半岭形曲线($\lambda = {e^{ - {{\left(\tfrac{x}{\sigma }\right)}^2}}}$)动态生成插值因子$\lambda$。最后，根据插值法原理插值，生成更多的概念方案解：

式中：${\boldsymbol{x}}_k^{(t)}$为第t个子凸包内插入的新的方案；${\boldsymbol{x}}_c^{(t)}$为模糊聚类中心方案；${{\boldsymbol{x}}_{p'}}$与${{\boldsymbol{x}}_{q'}}$为子凸包空间内相邻的2个向量。

1.3   本研究创新性

1） 在文献[18]中，杨萌等提出在船舶概念方案设计过程中仅考虑性能对设计参数的影响，弱化了用户的实际需求；这种方式导致实际生成的船舶概念方案解在一定程度上会偏离用户的需求，而在船舶概念方案设计过程中，用户需求往往扮演着非常重要的角色，其重要性不可小视，甚至对船舶概念方案设计起决定性的作用。因此，本研究设计一种类栈式结构的性能参数值推理模型，既考虑了性能对船舶概念方案设计的影响，也强化了用户对船舶设计方案的真实表征；

2） 文献[18]仅考虑船舶概念方案设计过程中设计型参数与母型船之间简单的一对多映射关系，在一定程度上会割裂不同设计参数间的耦合关系；由于在模糊推理过程中，推理的结果应与实际的母型船一一对应；因此，本研究既充分挖掘模糊推理结果与母型船间的共性关系，又考虑了用户的实际需求。

2.   算例验证

本研究所提出的模糊推理系统是一套单向生成系统，其中不包括参数训练的过程，所有参数均为提前设定的超参数，在此基础上将模拟的用户需求作为输入数据，验证整个船型设计模糊推理的过程以及性能。

2.1   算例描述

本文所构建的数据库来源于公开船型数据以及船型设计仿真数据。该数据库包括2个子库，分别为船型性能参数库和船型设计参数库。船型性能参数库由12条船的排水量、续航里程等12个性能参数构成。船型设计参数库由120条船的船长、船宽等68个设计参数构成。2个子库之间的样本存在对应关系，一条性能参数值，对应设计参数库中10条船的设计参数值，该对应关系由船舶领域专家根据专业知识设定。

因为无法获取直接的用户需求以及用户需求的性能数值所对应的设计参数，所以本研究考虑用母型船库中的某一条性能参数值来模拟用户需求，作为整个模糊推理系统的输入。模型的输入是由性能参数值以及模糊语言变量构成，除了性能参数库中的性能数值外，还需将模糊语言变量全部设置为“等于”，如表2所示。

表  2  模拟用户需求

Table  2.  Simulated user requirements

算例	船型性能	性能数值	语言变量
1	排水量	7 200/t	等于
	续航里程	9 000/km	等于
	稳性约束	1.25	等于
	操纵性	8.6	等于
	……	……	……
	尾垂发	24	等于
	近防炮	2.2	等于
	舰载机规格	3	等于
2	排水量	6 000/t	等于
	续航里程	6 000/km	等于
	稳性约束	1	等于
	操纵性	8	等于
	……	……	……
	尾垂发	16	等于
	近防炮	2	等于
	舰载机规格	2	等于

下载: 导出CSV 

| 显示表格

船型性能参数库与设计参数库存在对应关系，如表3所示。在性能参数推理过程中利用FCM生成模糊聚类中心以及方差，FCM相关参数设置见表4。通过观察模型推理所得的设计方案与母型船设计参数库中的设计方案的差异，帮助本文评估模糊推理系统的推理偏差与合理性。

表  3  模拟用户需求船型性能数值对应母型船设计参数库中的设计参数值

Table  3.  Corresponding design parameters in parent vessel database for simulated user requirement hull performance values

算例	设计参数	期望值
1	船长/m	157.9
	船宽/m	15.9
	型深/m	11.6
	吃水/m	5.8
	……	……
	舷侧倾斜角19	18.5
	舷侧倾斜角22	16.35
2	船长/m	154.5
	船宽/m	15.9
	型深/m	11.6
	吃水/m	5.8
	……	……
	舷侧倾斜角19	20.38
	舷侧倾斜角22	18.28

下载: 导出CSV 

| 显示表格

表  4  FCM参数设置

Table  4.  Parameter settings of FCM

参数名称	参数值
模糊权重/m	1.7
迭代最大伦次	1 000
收敛阈值\$	0.000 01

下载: 导出CSV 

| 显示表格

2.2   算性能参数推理

本研究在算例中与文献[18]的性能参数推理误差进行对比。通过表5可以看到，经本研究优化后，系统在模糊语言变量全部为“等于”时，模糊推理系统第1阶段推理所得的性能参数值与模拟用户需求的性能数值相近，表明本研究提出的系统在第1阶段模糊推理中具备对用户性能需求的建模能力，能够准确地推理出用户的性能需求。同时对比文献[18]的模糊推理系统所推理得出的性能参数值，在绝大多数性能参数上相对模拟用户需求的性能参数偏差更小。该结果表明，本研究提出的模糊推理系统能够更加准确地捕捉到用户的性能需求。

表  5  模糊推理性能数值与模拟用户需求性能数值对比

Table  5.  Comparison of fuzzy inference performance indicators and simulated user requirement parameters

算例	船型性能	性能数值	模糊推理值 （本研究）	模糊推理值 （文献[18]）
1	排水量/t	7 200	7 222	70 58
	续航里程/km	9 000	9 061	8 613
	稳性约束	1.25	1.253	1.23
	操纵性	8.6	8.61	8.5
	……	……	……	……
	尾垂发	24	24.08	23.48
	近防炮	2.2	2.202	2.18
	舰载机规格	3	3.02	2.87
2	排水量/t	6000	6012	6193
	续航里程/km	6000	5760	6254
	稳性约束	1	1.09	1.11
	操纵性	8	8.06	8.14
	……	……	……	……
	尾垂发	16	19.68	20.34
	近防炮	2	2.09	2.11
	舰载机规格	2	1.92	2.08

下载: 导出CSV 

| 显示表格

2.3   船型设计参数模糊推理

将本研究提出的模糊推理系统的第1阶段用户需求性能参数模糊推理作为第2阶段船型设计参数模糊推理的输入，将性能参数映射到相应的设计参数。对比本研究与文献[18]的设计参数偏差，如表6所示。本研究提出的系统推理生成的设计参数值与预期的设计参数值的偏差明显小于文献[18]。该结果表明经过改进的船型设计方案模糊推理系统能够根据用户的需求生成相对应的船型设计方案，同时相比较未加入类栈式结构的系统具有更高的推理准确度。

表  6  模糊推理所得船型设计参数与模拟用户需求对应设计参数对比

Table  6.  Comparison of hull design parameters from fuzzy inference and simulated user requirement design parameters

算例	设计参数	期望值	模糊推理值 （本文）	模糊推理值 （文献[18]）
1	船长/m	142.8	141.37	148.79
	船宽/m	15.7	15.83	15.91
	型深/m	11.6	11.54	11.68
	吃水/m	5.8	5.86	5.83
	……	……	……	……
	舷侧倾斜	17.87	17.9	18.35
	角19	19.86	19.79	18.67
2	船长/m	154.5	154.8	158.48
	船宽/m	15.9	15.95	16.05
	型深/m	11.6	11.6	11.7
	吃水/m	5.8	5.79	5.83
	……	……	……	……
	舷侧倾斜	20.38	19.05	18.52
	角19	18.28	18.43	18.37

下载: 导出CSV 

| 显示表格

2.4   船舶设计合理性判断

本研究提出的船舶设计方案生成系统通过模糊推理将用户需求转化为性能参数，再映射为船型设计参数。当需要同时满足两个性能需求时，系统通过模糊逻辑“and”运算从母型船参数库中筛选出同时符合两者的设计参数组合。然而，由于设计参数间存在耦合关系，满足一个性能需求的设计调整可能会限制另一性能需求的完全实现。因此，船舶设计方案推理系统最终所得到的结果，存在不符合实际设计标准的可能性，需要对所生成的方案进行合理性优化，以便筛选出既符合用户需求又满足船舶设计标准的设计方案。

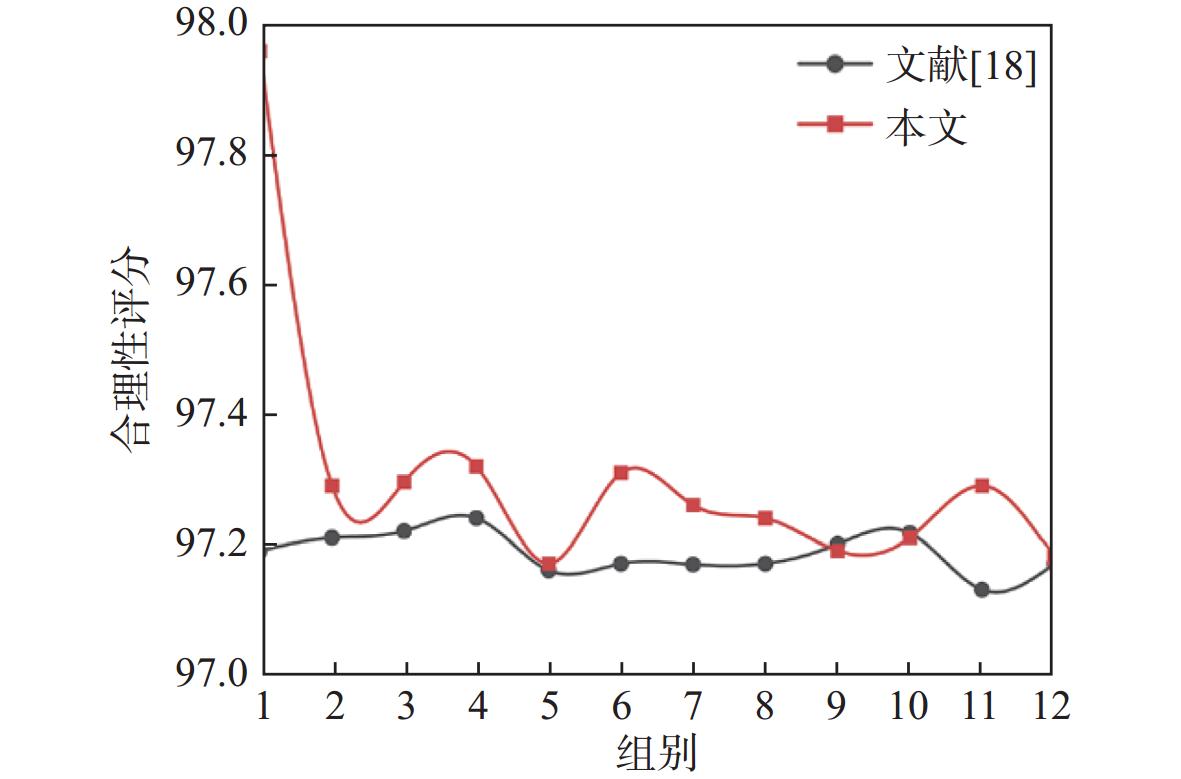
本文将性能参数库及母型船设计方案库划分为12组数据，每组数据包括一条模拟用户需求的性能参数值及其对应的船型方案和用于模拟现有参数库的剩余性能参数值及其对应的设计方案。对比本研究与文献[18]推理得到的船型设计方案与最近同类母型船每个设计参数之间的平均偏差，来验证二者的设计合理性。

合理性评分计算公式如下：

式中：${\boldsymbol{DP}}_i^{\rm{infer}}$表示推理方案的第i个设计参数；${\boldsymbol{DP}}_i^{\rm{Par}}$表示母型船方案的第i个设计参数；N表示一条船共有N个船型设计参数。

如图3所示，12组数据在经过本研究优化后模型生成的船型概念方案的合理性评分明显高于文献[18]的模型。算例结果表明，本研究提出的船型概念方案设计模糊推理系统能够保证生成的设计方案在满足用户需求的同时，符合概念方案设计的合理性。

图  3  优化与未优化方案合理评分对比图

Figure  3.  Comparison of rationality scores between optimized and non-optimized solutions

下载: 全尺寸图片 幻灯片

3.   结　论

本文针对船舶概念方案设计的传统方法存在的时间成本高、设计过程复杂等问题，提出了一套船舶概念方案快速模糊推理系统。通过引入类栈式结构减少了推理过程中性能参数推理部分可能出现的错误推理，强化了用户需求的性能参数在设计参数推理中的影响。利用聚类算法对推理所得概念方案进行合理性优化，保证了概念方案的有效性和科学性。算例验证表明，本研究提出的船型概念方案模糊推理系统相比文献[18]在性能参数推理和设计参数映射上具有更小的偏差，提高了其推理准确性。同时本研究提出的推理系统所生成的船型概念方案相比文献[18]的系统具有更高的设计合理性。本研究不仅在理论上丰富了船舶概念方案设计的优化方法，也为实际应用提供了有效的支持，能够更好地满足日益多样化的船舶功能需求，提高设计效率和减少人力成本，为船舶设计提供了新的思路。

尽管本研究提出的模糊推理系统在船舶概念方案设计中表现出较好的性能参数推理准确性和方案，但该系统中第2阶段模糊推理中的“and”算子任然存在无法耦合多个参数的局限性。本研究从“and”算子的后端对该问题进行了优化，在将来的工作中，我们会对“and”算子的直接优化进行研究，以进一步提升船型概念方案的合理性。此外，本研究在两个阶段的模糊推理之间引入了类栈式结构，未来我们考虑构建具有栈式结构的多层次模糊推理系统。