Research on optimization of intelligent anchorage management for ships based on OBS-MLP fusion algorithm
-
摘要:目的
针对海上风电施工中多船抛锚协同决策效率低、安全风险高的难题，提出一种基于最优脑手术剪枝算法−多层感知机（OBS-MLP）融合算法的智能化锚位管理方法。
方法首先，构建“特征解耦−动态剪枝−偏好决策”三级优化框架，融合决策树与神经网络优势，通过OBS剪枝策略降低模型参数冗余度，解决传统算法在高维决策空间中的"维度灾难"问题；其次，建立多模态特征融合机制，实现环境静态特征与动态交互特征的分层提取与协同优化；最后，设计混合整数规划约束下的偏好决策模型，以量化不同调整策略的经济性与安全性权重。
结果以广东某海上风场为例，算法平均精确率达到95.3%（较单一算法提升8.05%），平均响应时间缩短至0.9 s（提升30.77%），年减少潜在经济损失约24万元，有效降低了船舶抛锚作业中的安全风险。
结论该研究可为多船抛锚协同优化提供高效解决方案，推动海上安全管理的数字化转型。
Abstract:ObjectiveTo address the low efficiency and high safety risks associated with multi-ship anchoring during offshore wind farm construction, an intelligent anchoring management method is proposed based on an optimal brain surgery-multi-layer perceptron (OBS-MLP) fusion algorithm.
MethodInitially, a three-level optimization framework of feature decoupling-dynamic pruning-preference decision was constructed, integrating the advantages of decision trees and neural networks. This framework uses OBS pruning strategies to reduce model parameter redundancy, thus overcoming the curse of dimensionality faced by traditional algorithms in high-dimensional decision spaces. Subsequently, a multi-modal feature fusion mechanism was established for the hierarchical extraction and collaborative optimization of static environmental features and dynamic interaction features. Finally, a preference decision-making model with mixed-integer programming constraints was designed to quantify the economic and safety weights of different adjustment strategies.
ResultsTaking an offshore wind farm in Guangdong as an example, the average accuracy of the algorithm is 95.3%, which is 8.05% higher than that of the individual algorithm. The average response time is shortened to 0.9 seconds, a 30.77% reduction. The potential economic loss is reduced by about 240 000 yuan per year, thereby effectively reducing safety risks in ship anchoring operations.
ConclusionThe research provides an efficient solution to multi-ship anchoring collaborative optimization and promotes the digital transformation of maritime safety management.
-
0. 引 言
船舶安全是维护海上交通秩序的核心议题。在复杂多变的海洋环境中，人为因素导致的操作失误与协同失效已成为事故防控的重点领域[1-6]。船舶安全技术研究主要包括防碰撞技术、通航安全分析以及网络信息安全等。在防碰撞技术方面，通过构建风险识别模型[7-8]，开发数值计算方法[9]以及提出智能决策支持系统[10-11]，提升航行风险防控能力。在通航安全分析领域，重点研究航行环境稳性评估[12]、风险概率建模[13]和特殊海况运动预报[14]。在网络信息安全方面，研究内容涉及网络安全评估模型[15-16]、AI驱动的防御体系[17]和基于智能优化的网络能源稳定技术[18-19]。
在船舶调度领域，现有研究多聚焦于进出港优化问题，如基于智能算法的泊位分配[20-21]、航速协同优化[22]和航道通过效率提升[23-24]等方面，已形成较为完整的理论体系。相比之下，面向多船抛锚协同调度的研究仍处于起步阶段。
近年来，抛锚安全研究在三维锚位检测、数字化管理及风险防控等方面取得了阶段性进展。在锚位感知领域，基于遍历算法与蒙特卡洛算法的三维锚位动态识别技术[25-26]及UNITY3D平台验证的锚位保持系统[27]，初步实现了锚链张力与海底地形的耦合分析；项目级船舶管理平台[28]通过锚位预约与水文数据融合，优化了静态锚地资源配置。在风险防控方面，人工智能优化的锚机结构设计[29]、恶劣海况安全评估模型[30]及海底管道拖拽损伤防护技术[31]，为走锚预警与危害防护提供了理论支撑。
然而，随着海上风电等海洋工程的发展，传统锚泊管理模式面临严峻挑战：1）现有技术多聚焦静态场景，三维检测系统对多船锚位空间干涉、锚链动态松弛度的实时反馈能力不足，导致密集锚地转向冲突频发；2）锚位管理平台依赖人工经验决策，响应延迟超过10 min，无法动态处理锚地资源碎片化与突发性锚位竞争问题；3）风险防控手段缺乏对多船干扰耦合效应的预判机制，现有模型难以同步处理风流压漂移叠加、连锁走锚等复杂工况。尤其是海上风电运维船与工程船在狭窄海域的锚泊作业，暴露出传统调度在动态协同决策上的根本缺陷：缺乏融合环境时变特性与船舶运动耦合的智能分配算法，且实时避碰决策仍停留在操作规范层面。
针对上述问题，本文拟通过构建特征解耦、动态剪枝与偏好决策三级优化框架，将最优脑手术剪枝算法（optimal brain surgeon，OBS）与多层感知机（multi-layer perceptron，MLP）进行融合，通过特征解耦模块消除冗余特征干扰，利用动态剪枝机制抑制决策树过拟合风险，并在偏好决策层实现多目标优化。该融合算法将结合MLP的高效分类能力与OBS的模型简化优势，在保持神经网络非线性拟合能力的同时，利用剪枝策略降低模型复杂度，最终通过互补信息处理增强决策鲁棒性[32-35]。通过海上风场的实际应用案例，验证该算法在提升船舶抛锚决策精度和效率方面的效果。
1. 目标智能体
1.1 定义问题
1.1.1 抛锚冲突模型
针对多因素船舶干扰问题，双船交叉影响因素主要分为两大类：外界环境干扰（如海风、海浪、海流）和空间干扰（如两船抛锚的位置）。已有学者针对环境因素对船舶的影响进行了模型研究与分析，但关于空间干扰对船舶影响的研究成果尚未见报道[36]。在双船抛锚作业过程中，尤其是在锚泊间距不足的情况下，若发生走锚导致的偏航位移，将显著提升船舶间碰撞概率，对港口水域航行安全构成严重威胁。
运输船锚位长度取500 m，锚位空间定义为
Ai={(xi,k,yi,k)|k=1,2,3,4} (1) 起重船锚位长度取1 000 m，锚位空间定义为
Aj={(xj,l,yj,l)|l=1,2,…,6} (2) 两船冲突风险度为\$
Rij=Ki∑k=1Kj∑l=111+e−α(dkl−dsafe) (3) 式中：dkl=‖； \alpha 为风险敏感系数，取为1； {d}_{\mathrm{s}\mathrm{a}\mathrm{f}\mathrm{e}} 为安全距离阈值，为避免因为走锚造成船舶碰撞， {d}_{\mathrm{s}\mathrm{a}\mathrm{f}\mathrm{e}} 取为0。
1.1.2 可能行动
定义运输船后继函数 T(X) 为一个由有序对 \langle{A(X),B(X)}\rangle 组成的集合，其中 A(X) 为行动函数， B(X) 为采取行动后的状态函数。则
T(X)=\left\{\begin{array}{c}\langle{A({X}_{1}),B({{X}_{1}'},{X}_{2},{X}_{3},{X}_{4})}\rangle,\\ \langle{A({X}_{2}),B({X}_{1}{{,X}_{2}'},{X}_{3},{X}_{4})}\rangle,\cdots ,\\ \langle{A({{X}_{1}'}{{,{{X}_{2}'},X}_{3}'},{{X}_{4}'}),B({{X}_{1}'}{{,{{X}_{2}'},X}_{3}'},{{X}_{4}'})}\rangle\end{array}\right\} (4) T(Y)=\left\{\begin{array}{c}\langle{A({Y}_{1}),B({{Y}_{1}'},{Y}_{2},{Y}_{3},{Y}_{4},{Y}_{5},{Y}_{6})}\rangle,\\ \langle{A({Y}_{2}),B({Y}_{1}{{,Y}_{2}'},{Y}_{3},{Y}_{4},{Y}_{5},{Y}_{6})}\rangle,\\ \langle{A({Y}_{3}),B({Y}_{1},{Y}_{2}{{,Y}_{3}'},{Y}_{4},{Y}_{5},{Y}_{6})}\rangle,\\ \cdots ,\left\langle{\begin{array}{c}A({{Y}_{1}'}{{,{{Y}_{2}'},Y}_{3}'},{{Y}_{4}'},{{Y}_{5}'},{{Y}_{6}'}),\\ B({{Y}_{1}'}{{,{{Y}_{2}'},Y}_{3}'},{{Y}_{4}'},{{Y}_{5}'}{{,Y}_{6}'})\end{array}}\right\rangle\end{array}\right\} (5) 其中， T(X) 包含 {C}_{4}^{1}+{C}_{4}^{2}+{C}_{4}^{3}+{C}_{4}^{4}=15 种状态， T(Y) 包含 {C}_{6}^{1}+{C}_{6}^{2}+{C}_{6}^{3}+{C}_{6}^{4}+{C}_{6}^{5}+{C}_{6}^{6}=63 种状态。
1.1.3 目标测试
研究目标为防止运输船与起重船的锚位交叉。为抑制船舶偏荡，运输船双锚夹角应控制在90°～120°，起重船双锚夹角应控制在60°～90°。为简化计算，将船舶假想为一个圆，根据两船圆心距离d判定锚位调整需求：
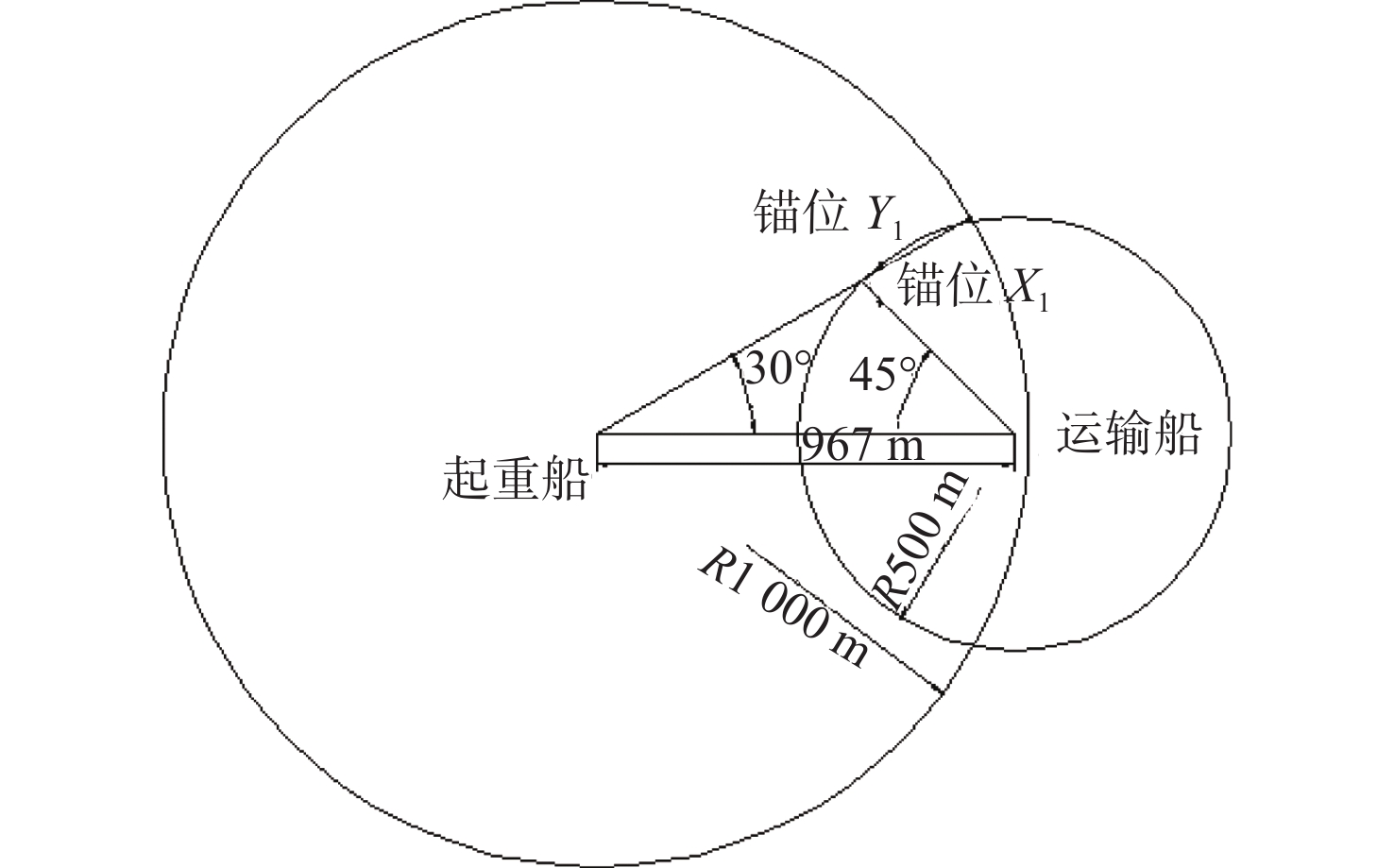
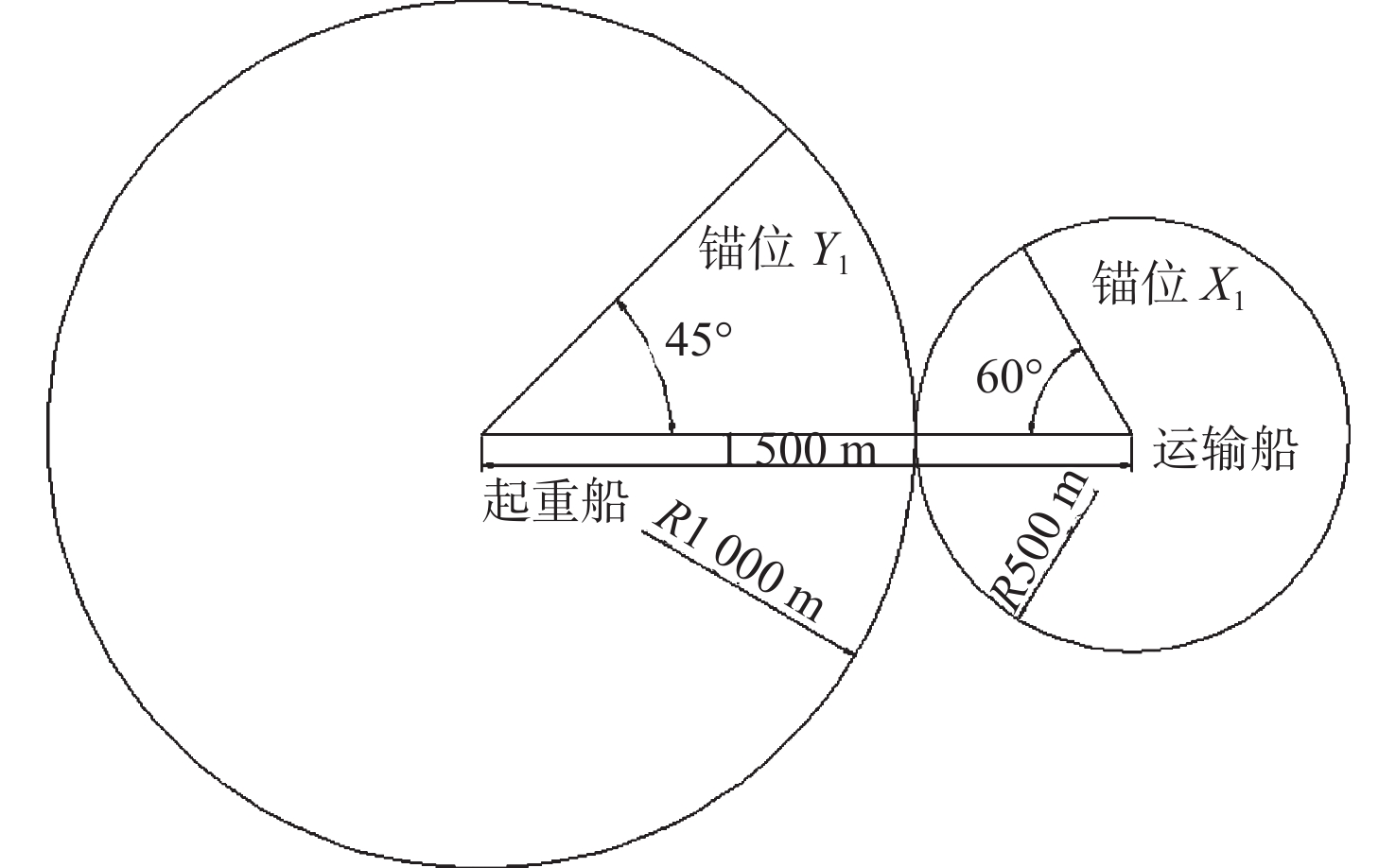
1）当 d\gg 1 \;500\;\mathrm{m} 时，两船锚位不会发生交叉，无需进行锚位调整，如图1所示。
![]()
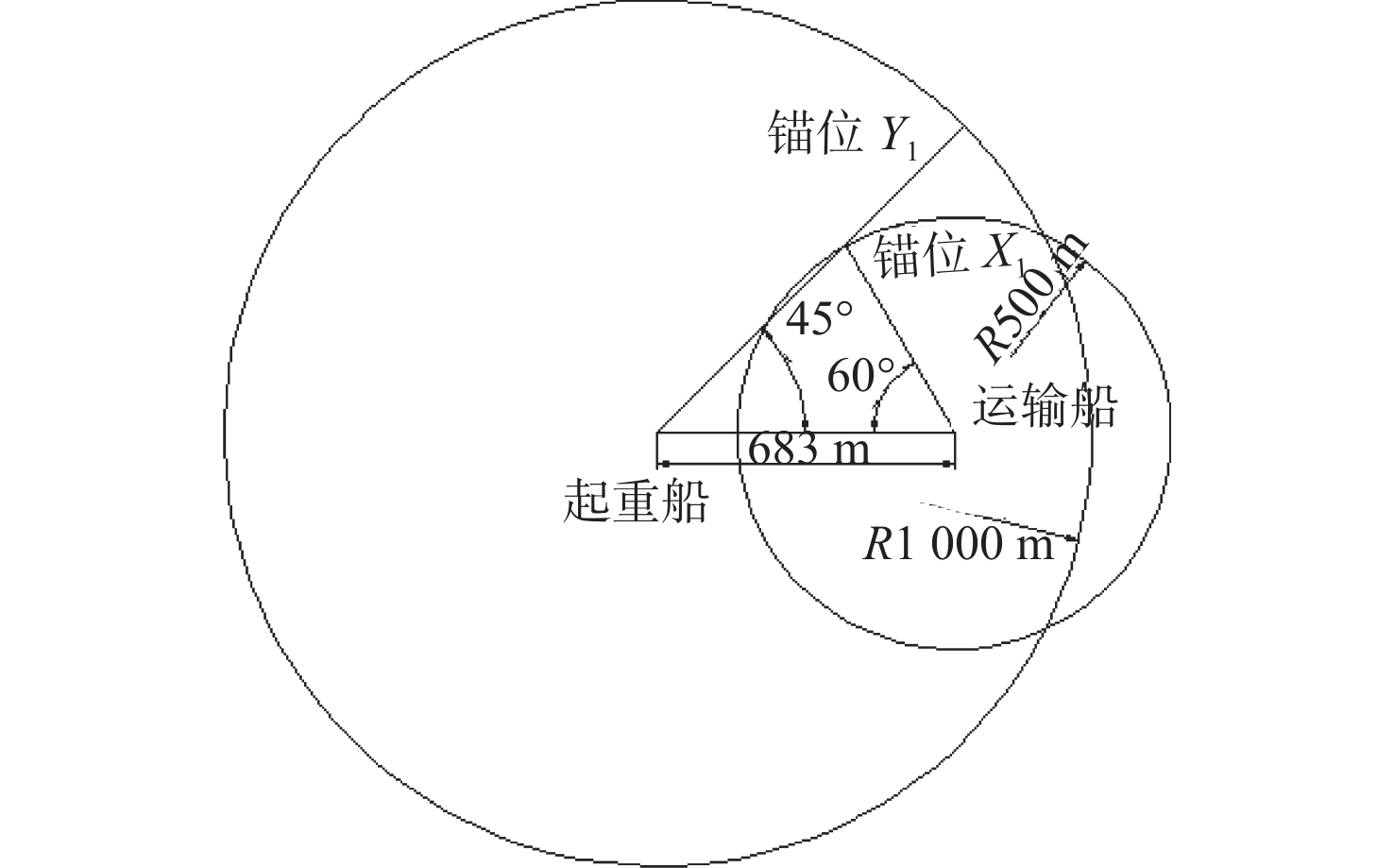
图 1 两船相对状态一示意图Figure 1. Schematic diagram of relative positions between two vessels (Case 1)2）当 d=967\;\mathrm{m} 时，起重船双锚夹角调整为60°，运输船双锚夹角调整为90°，两船锚位不会发生交叉（图2）；当 967\;\mathrm{m}\le d < 1 \;500\;\mathrm{m} 时，两艘船的锚位可能会发生交叉，此时需要调整其中一艘船的双锚夹角才能避免交叉。
![]()
图 2 两船相对状态二示意图Figure 2. Schematic diagram of relative positions between two vessels (Case 2)3）当 d=683\;\mathrm{m} 时，起重船双锚夹角调整为90°，运输船双锚夹角调整为120°（均为最大夹角），两船锚位不会发生交叉（图3）；而当 683\;\mathrm{m}\ll d < 967\;\mathrm{m} 时，两船锚位会发生交叉，此时需要调整两艘船的双锚夹角才能避免其发生交叉。
![]()
图 3 两船相对状态三示意图Figure 3. Schematic diagram of relative positions between two vessels (Case 3)4） 当 d < 683\;\mathrm{m} 时，两船锚位会发生交叉，此时需要调整d，使 d\gg 683\;\mathrm{m} 。
1.2 智能体模型
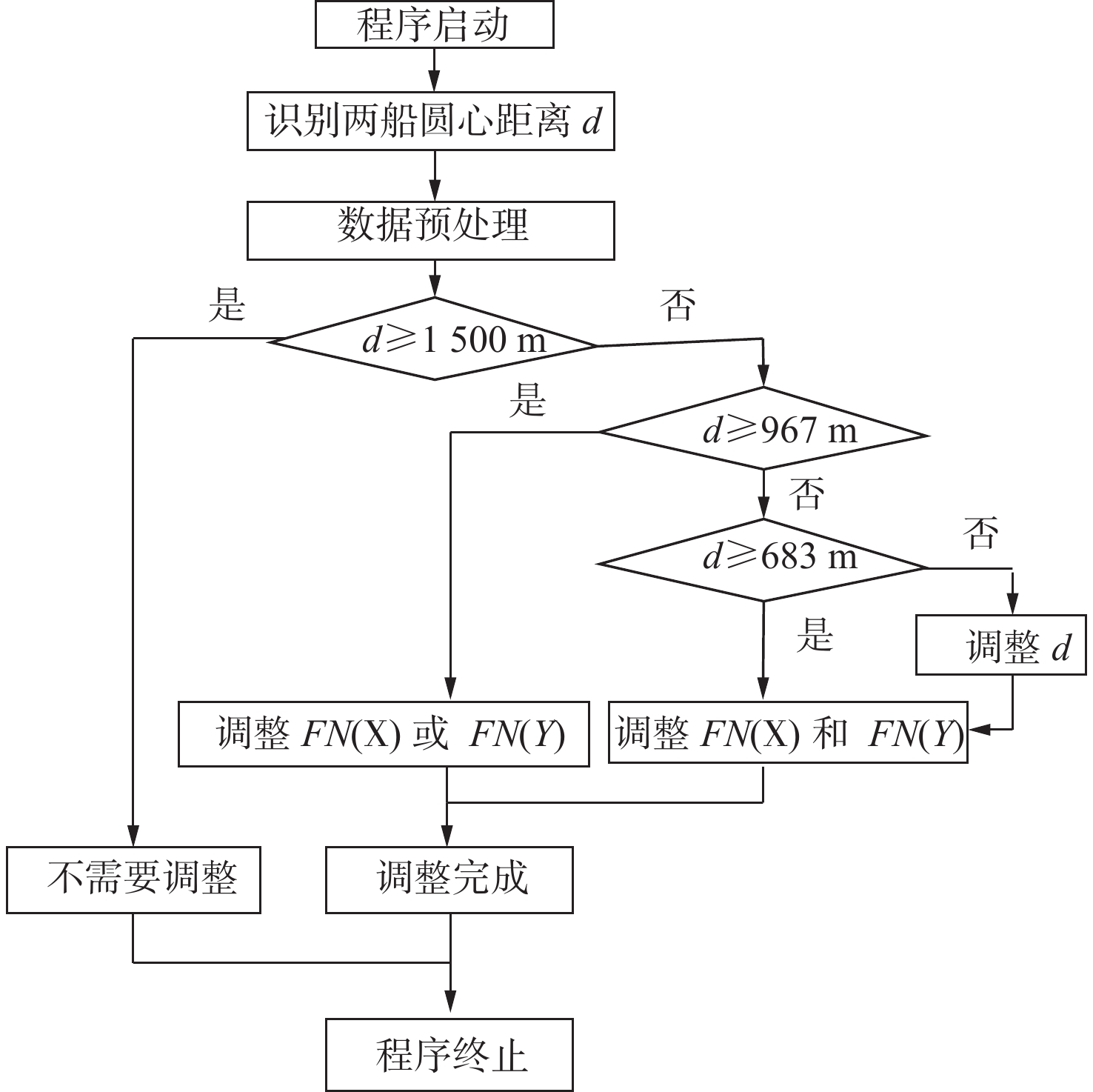
结合上述不同抛锚场景，构建智能体模型，如图4所示。
由图4可见，只调整一艘船的双锚夹角时，即调整 {F}{N}(X) 或 {F}{N}(Y) ，有 15+63=78 种方式；同时调整两艘船的锚位双锚夹角时，即调整 {F}{N}(X) 和 {F}{N}(Y) ，有 15\times 63=945 种方式。因此，两船抛锚调整方案多达
1023 种，依靠传统计算无法高效确定最佳方案，而人工智能（AI）技术在这方面具有强大优势。2. 决策树−神经网络融合算法
2.1 偏好约束
考虑到起重船起抛锚效率一般低于运输船，设置偏好约束为
\sum_{m=0}^4 \sum_{n=0}^6(J_m+K_n) \cdot w_{m, n} \leq \mathrm{C} (6) 式中： {J}_{m} 为运输船调整次数为m的代价权重， m\in \{\mathrm{0,1},\mathrm{2,3},4\} ； {K}_{n} 为起重船调整次数为n的代价权重， n\in \{\mathrm{0,1},\mathrm{2,3},\mathrm{4,5},6\} ； {w}_{m,n} 为二进制决策变量，表示是否选择运输船调整m次且起重船调整n次的策略， {w}_{m,n}\in \{\mathrm{0,1}\} ；C为总调整代价阈值，C取为8。
引入混合整数规划用于量化锚位调整的偏好权重，量化经济性与安全性权重，目标函数为
\underset{w}{\mathrm{min}}\sum _{k=1}^{K}[\rho \cdot {E}_{\mathrm{M}\mathrm{S}\mathrm{E}}(w)+\beta \cdot {\|w\|}_{0}] (7) 式中： \rho 为经济性权重系数， \rho 取为1.2（通过网格搜索）； {E}_{\mathrm{M}\mathrm{S}\mathrm{E}}(w) 为均方误差项； \beta 为安全性权重系数， \beta 取为0.05； {\|w\|}_{0} 为权重向量中非零元素的数量，用于简化模型结构。
2.2 四层前馈神经网络
定义行动A具有若干可能的状态 {R}_{i}(A) ，其中索引i代表不同结果的数量。执行A之前，智能体为每个结果赋予概率 P({R}_{i}(A))|A) ，则该行动的期望效用 R(A|E) 为
R(A|E)=\sum _{i}P({R}_{i}(A))|A)\times \cup {R}_{i}(A) (8) 根据最大期望效用（MEU）原则，通过枚举所有可能的行动序列，选择使智能体期望效用最大化的行动。
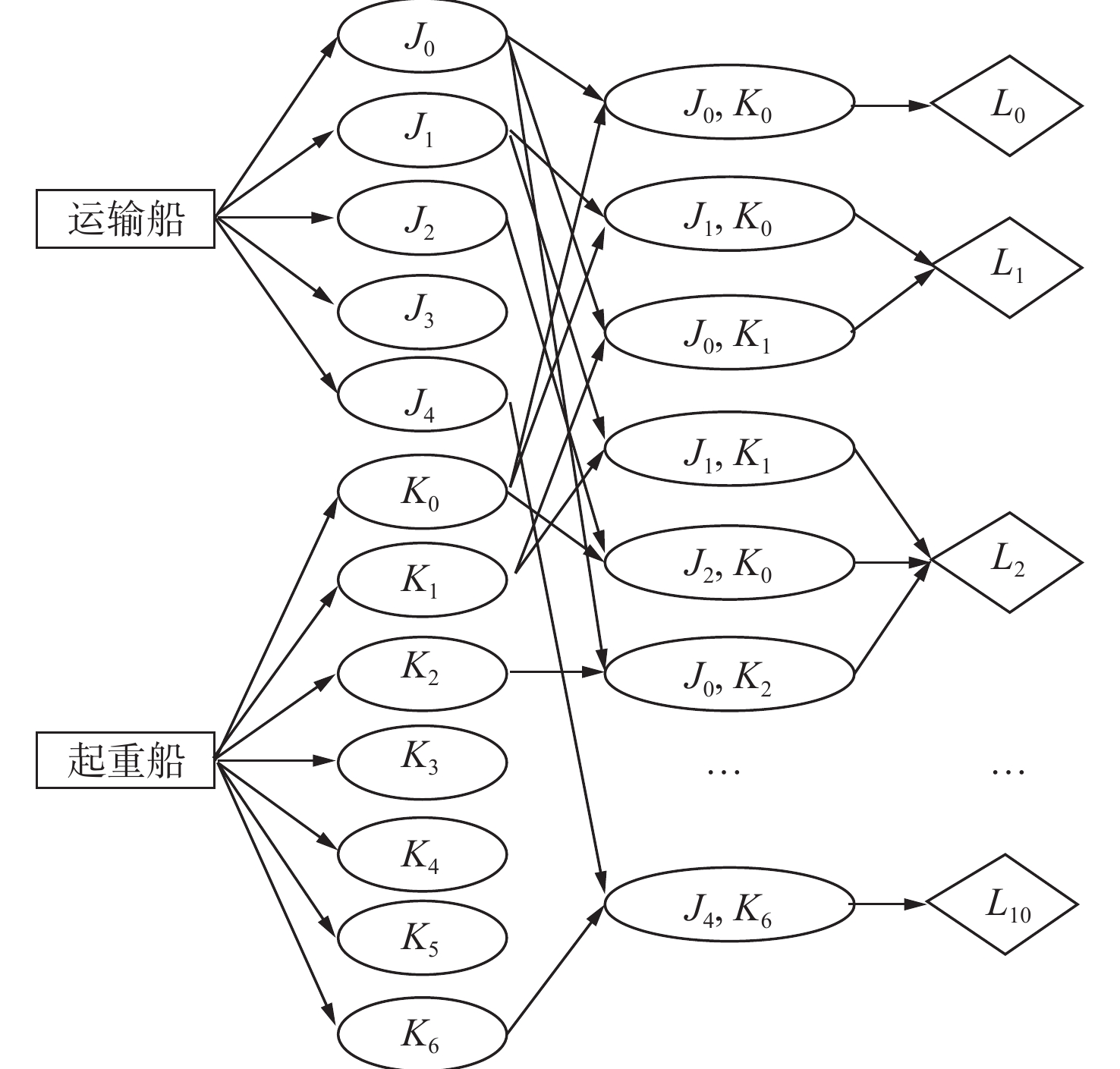
根据决策树理论，决策树的每个分裂条件确定一个超平面的方向和位置，而由一系列这样的条件（即一条路径）所构成的规则，则描述了一个更复杂、多维度的超平面，用于在特征空间中进行精确的数据分割和分类。基于上述规则，构建了一个四层前馈神经网络，如图5所示。
在图5中，输入层节点对应问题的特征属性，如运输船的特征；第1层节点对应决策树中不重复的非叶子节点，如 {J}_{0} ；第2层节点对应决策树的叶子节点，如 ({J}_{1},{K}_{0}) ；输出层节点对应不重复的类别标签，如 {L}_{1} 代表锚位调整1次的组合集。其中 {L}_{0} > {L}_{1} > {L}_{2} > {L}_{3} > \cdots > {L}_{10} 。
2.3 决策树模型
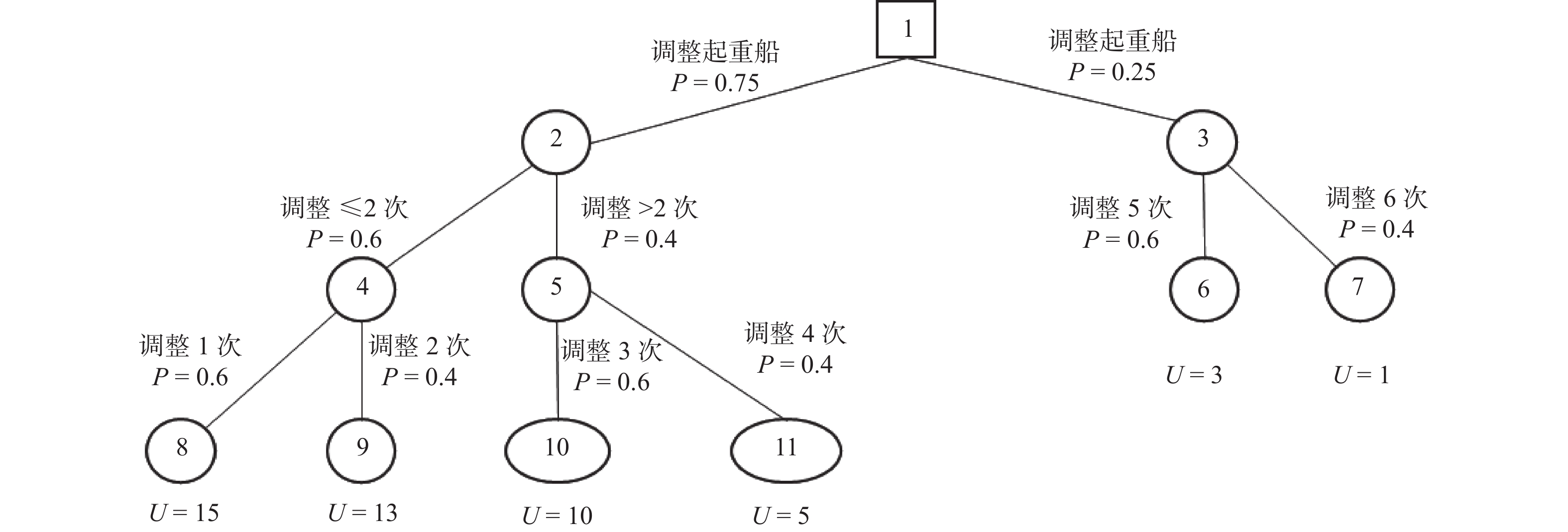
以调整一艘船的锚位为目标，建立决策树模型。并验证模型，计算各个节点的期望效用：
R({\minchofont\text{⑧}})=0.6\times 0.6\times 15=5.40 R({\minchofont\text{⑨}})=0.6\times 0.4\times 13=3.12 R({\minchofont\text{⑩}})=0.4\times 0.6\times 10=2.40 R({\minchofont\text{⑪}})=0.4\times 0.4\times 5=0.80 R({\minchofont\text{⑫}})=0.6\times 0.6\times 14=5.04 R({\minchofont\text{⑬}})=0.6\times 0.4\times 12=2.88 R({\minchofont\text{⑭}})=0.6\times 0.5\times 0.4\times 9=0.86 R({\minchofont\text{⑯}})=0.4\times 0.4\times 0.6\times 4=0.38 R({\minchofont\text{⑱}})=0.4\times 0.4\times 0.4\times 0.6\times 3=0.12 R({\minchofont\text{⑲}})=0.4\times 0.4\times 0.4\times 0.4\times 1=0.03 (9) R({\minchofont\text{⑧}}) > R({\minchofont\text{⑫}}) > R({\minchofont\text{⑨}}) > R({\minchofont\text{⑬}}) > R({\minchofont\text{⑩}}) > R({\minchofont\text{⑭}}) > R({\minchofont\text{⑪}}) > R({\minchofont\text{⑯}}) > R({\minchofont\text{⑱}}) > R({\minchofont\text{⑲}}) ，结果满足偏好约束，模型通过验证。
2.4 剪枝策略优化
由于决策树训练数据中存在噪声，有必要对决策树进行剪枝。在保持精度的前提下，对不必要的数据分枝进行处理，以简化决策树结构。剪枝后的决策树规模更小，有利于提升预测计算速度。具体优化策略如下：
1） 收集与挖掘目的相关数据，并将其分为训练和测试样本；
2） 对训练和测试样本进行数据预处理，转换成统一的结构形式；
3） 使用训练样本对决策树进行训练；
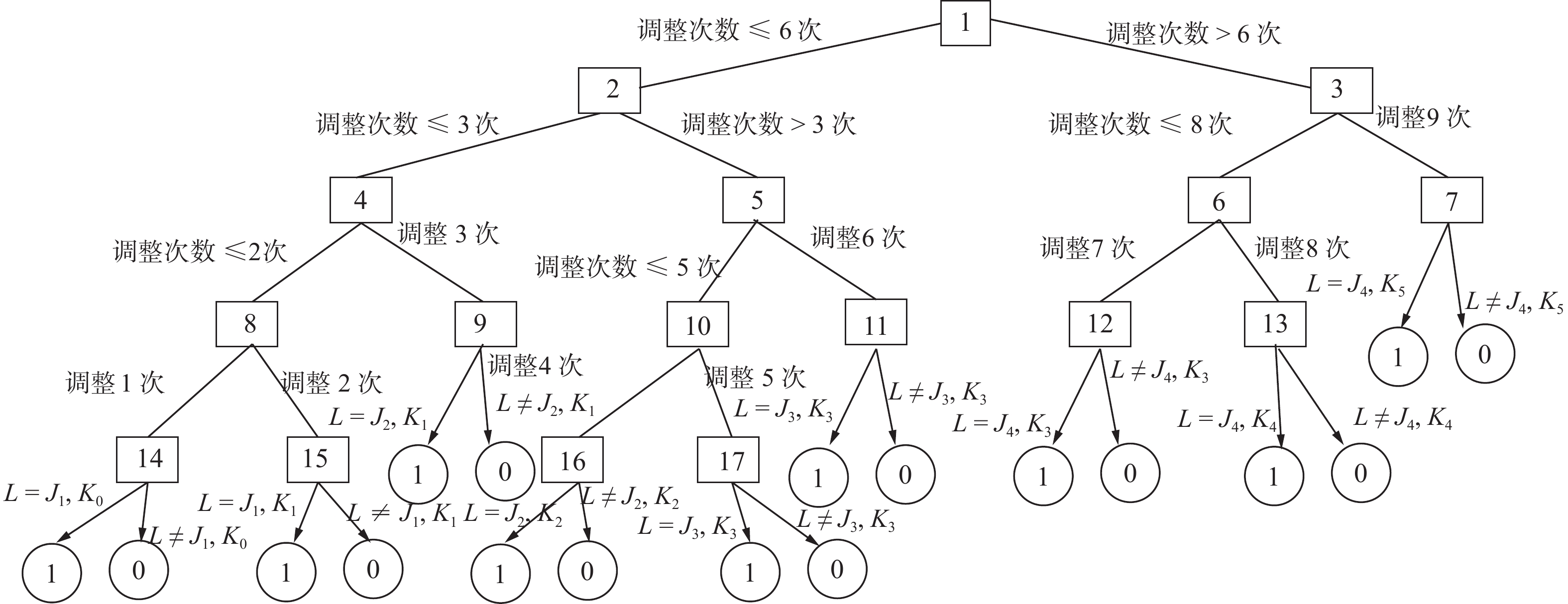
4） 采用最优脑手术（OBS） 剪枝算法对决策树进行剪枝，得到优化后的决策树，如图6所示。
R({\minchofont\text{⑧}}) > R({\minchofont\text{⑨}}) > R({\minchofont\text{⑩}}) > R({\minchofont\text{⑪}}) > R({\minchofont\text{⑥}}) > R({\minchofont\text{⑦}}) ，结果满足偏好约束，剪枝后的模型通过验证。
3. 实证分析
3.1 工程概况
广东某海上风电场示范项目位于粤东海域，场址面积约为60 km2，水深在30～40 m之间，离岸距离约为25 km。风电场规划装机总容量为750 MW，包括64台风机，并配套建设一座220 kV海上升压站。
在项目建设高峰期，风电场内同时有45艘船舶作业，其中包括7艘起重船和15艘运输船，风机机位点间距为1.5 km，在相邻机位施工时，船舶调度存在较大的安全管理风险。在项目建设周期内，累计审批船舶调度495次，其中涉及起重船与运输船之间的锚位交叉调整192次。
3.2 模型建立
3.2.1 样本选取
从192次锚位申请数据中随机选取100次作为训练样本，剩余92次作为测试样本。训练集与测试集规模相近，能够避免小样本下的过拟合风险，并通过5折交叉验证模型的稳定性。利用测试样本验证模型的有效性及精确率。
3.2.2 变量设置
在船舶安全的前提下，将最优的抛锚调整方案视为目标变量，即以起重船与运输船的抛锚调整次数为衡量标准。当调整方案最优时，标签值设为1；否则，标签值设为0。
第1类错误是指将非最优方案误标记为最优方案，第2类错误是指将最优方案误标记为非最优方案。第1类错误造成的实际损失更大。
3.2.3 数据预处理
首先，裁剪不必要的信息，如调整次数为 {L}_{0} 和 {L}_{10} 。经过筛选，保留97个训练样本（其中83个为最优方案、14个为非最优方案）和90个测试样本（其中75个为最优方案、15个为非最优方案）。其次，因为船上GPS定位设备通常安装在船桥甲板上（非船舶中心位置），需根据不同船舶的GPS定位设备安装位置对船舶进行拟合，确定船舶的圆心，并计算两船圆心距离d。
3.2.4 构建最优决策树
基于决策树和神经网络融合的船舶调度安全管理模型构建的最优决策树如图7所示。
在该决策树下，训练样本的精确率如表1所示。由表可见，模型分类结果正确的样本有95个，分类错误的样本有2个。
表 1 训练样本的整体精确率Table 1. Overall accuracy of the training samples判断结果 样本个数 精确率/% 正确 95 97.9 错误 2 2.1 总计 97 100.0 训练样本的重合矩阵如表2所示，在14个非最优方案中，有1个非最优方案被误标记为最优方案，概率为7.1%，13个被正确分类为非最优方案，精确率为92.9%；在83个最优方案中，有1个最优方案被误标记为非最优方案，概率为1.2%；其余82个被正确分类为最优方案，精确率为98.8%。
表 2 训练样本的重合矩阵Table 2. Confusion matrix of the training samples实际分类 预测结果 0 1 样本个数 占比/% 样本个数 占比/% 0 13 92.9% 1 7.1% 1 1 1.2% 82 98.8% 平均精确率 95.9% 由表2可知，训练样本平均精确率为95.9%，精确率为98.8%，召回率为98.8%，F1分数为98.8%，出现第1类错误概率为7.1%，出现第2类错误概率为1.2%，错误率较低，模型的预测效果较好。
3.3 有效性验证
运用构建的决策树对90个测试样本进行测试和评估，验证其在实际应用中的有效性。测试样本的重合矩阵如表3所示。
表 3 测试样本的重合矩阵Table 3. Confusion matrix of the test samples实际分类 预测结果 0 1 样本个数 占比/% 样本个数 占比/% 0 14 93.3 1 6.7 1 2 2.7 73 97.3 平均精确率 95.3% 根据表3可知，测试样本的平均精确率为95.3%，精确率为98.6%，召回率为97.3%，F1分数为98.0%，出现第1类错误的概率为6.7%，出现第2类错误的概率为2.7%，拟合效果较为理想。其中，第1类错误率较高主要由于训练样本中非最优方案占比不足（14/97）。例如，当两船锚位距离接近临界安全阈值（如967 m）时，动态海况扰动可能导致模型误判。
3.4 对比分析
分别运用OBS算法、MLP算法、CNN算法、LSTM算法对测试样本进行有效性验证，并与OBS-MLP算法结果进行对比分析，结果如表4所示，其中平均响应时间为输入锚位数据到输出调整策略的端到端计算耗时。
表 4 不同算法结果分析Table 4. Analysis of different algorithm results算法 平均
精确率/%平均响应
时间/s第1类
错误率/%第2类
错误率/%OBS 87.3 1.5 20.0 5.3 CNN 88.0 1.4 20.0 4.0 MLP 88.7 1.3 13.3 9.3 LSTM 91.3 1.1 13.3 4.0 OBS-MLP 95.3 0.9 6.7 2.7 由表4可见，采用OBS-MLP算法得到的平均精确率及平均响应时间显著优于其他算法，预测平均精确率提升8.05%，平均响应时间缩短30.77%，证明了融合算法的优越性。
为验证算法对安全风险的防控效果，统计传统人工调度与OBS-MLP算法得到的锚位冲突事件发生率、走锚预警延迟、安全距离达标率等指标结果的差异，结果如表5所示。
表 5 安全风险指标对比Table 5. Comparison of safety risk indicators算法 锚位冲突事件
发生率/%走锚预警
延迟/s安全距离
达标率/%人工调度 14.6 17.2 68.4 OBS-MLP 2.1 0.9 96.8 由表5可见，相比于传统人工调度方式，OBS-MLP算法能够使锚位冲突事件发生率降低85.62%，走锚预警延迟缩短94.77%，安全距离达标率提高28.4%，显著提升了锚位调整策略的安全性。
相比传统的人工调度方式，采用优化方案后，响应时间至少缩短了10 min。考虑到运输船与起重船的日均船机费用大约为35万元人民币，以及一个典型风场每年约需进行100次交叉抛锚作业的情况，仅在抛锚调度这一环节上，每年即可节省约24万元船机费用。这种效率的提升不仅减少了船舶等待时间，还显著降低了运营成本。
4. 结 论
传统海上安全管理体系通常聚焦于碰撞规避机制、航道通行效能优化及网络信息安全等显性风险防控领域。本研究通过构建海上施工场景下的船舶锚泊安全评估模型，系统论证了锚泊作业在海上安全链中的核心枢纽作用，为安全管理提供了新的研究视角。主要结论如下：
1） 锚泊作业的规范化管理不仅能通过提升泊位利用效率降低海上交通事故率，还能通过建立动态锚位分配算法优化海上交通资源调配效率。这一发现为构建基于风险预测的智能调度系统提供了理论支撑。
2） 在“特征解耦−动态剪枝−偏好决策”三级优化框架下，构建了OBS-MLP融合算法理论体系。该体系通过动态结合决策树与神经网络，并使用OBS剪枝策略减少冗余参数，有效应对高维决策空间的“维度灾难”；建立了多模态特征融合机制，分层提取环境静态和动态交互特征，实现协同优化；此外，引入混合整数规划约束的偏好决策模型，量化经济性和安全性权重，生成最优调整策略。该算法不仅提升了模型效率，还增强了决策的精确性和科学性。
3） 结合广东海上风电场的应用情况，OBS-MLP融合算法展现了显著优势。其平均精确率达到95.3%，相比单一算法提高8.05%；平均响应时间缩短至0.9s，相比单一算法缩短30.77%。与传统人工调度相比，锚位冲突发生率降低85.62%，安全距离达标率提高至96.8%，每年能避免约24万元的潜在经济损失。这一改进不仅提升了工作效率，还增强了海上作业的安全性。
未来计划开发一款船舶调度实时可视化系统，该系统不仅能够支持三维态势的推演，还能提供直观的风险评估和预警。同时，这一系统将与风场智能调度平台无缝对接，实现海上风电项目的规模化应用。通过这种集成方式，将大幅提升船舶管理的精确度和效率，进一步优化风场的整体运营，推动海上风电行业的智能化和高质量发展。
还可通过合成数据增强（如添加高斯噪声模拟海况波动）平衡样本分布，降低第1类错误率。进一步探索模型在Zero-shot场景下的泛化能力，同时结合元学习优化剪枝阈值，使其随数据分布动态调整，通过迁移学习适配不同海域的锚泊规则。
-
![]()
图 1 两船相对状态一示意图
Figure 1. Schematic diagram of relative positions between two vessels (Case 1)
![]()
图 2 两船相对状态二示意图
Figure 2. Schematic diagram of relative positions between two vessels (Case 2)
![]()
图 3 两船相对状态三示意图
Figure 3. Schematic diagram of relative positions between two vessels (Case 3)
表 1 训练样本的整体精确率
Table 1 Overall accuracy of the training samples
判断结果 样本个数 精确率/% 正确 95 97.9 错误 2 2.1 总计 97 100.0 
下载: 导出CSV
表 2 训练样本的重合矩阵
Table 2 Confusion matrix of the training samples
实际分类 预测结果 0 1 样本个数 占比/% 样本个数 占比/% 0 13 92.9% 1 7.1% 1 1 1.2% 82 98.8% 平均精确率 95.9%
下载: 导出CSV
表 3 测试样本的重合矩阵
Table 3 Confusion matrix of the test samples
实际分类 预测结果 0 1 样本个数 占比/% 样本个数 占比/% 0 14 93.3 1 6.7 1 2 2.7 73 97.3 平均精确率 95.3%
下载: 导出CSV
表 4 不同算法结果分析
Table 4 Analysis of different algorithm results
算法 平均
精确率/%平均响应
时间/s第1类
错误率/%第2类
错误率/%OBS 87.3 1.5 20.0 5.3 CNN 88.0 1.4 20.0 4.0 MLP 88.7 1.3 13.3 9.3 LSTM 91.3 1.1 13.3 4.0 OBS-MLP 95.3 0.9 6.7 2.7
下载: 导出CSV
表 5 安全风险指标对比
Table 5 Comparison of safety risk indicators
算法 锚位冲突事件
发生率/%走锚预警
延迟/s安全距离
达标率/%人工调度 14.6 17.2 68.4 OBS-MLP 2.1 0.9 96.8
下载: 导出CSV
-
[1] WU Z Z, WANG S Z, XU H, et al. Research on ship safety risk early warning model integrating transfer learning and multi-modal learning[J]. Applied Ocean Research, 2024, 150: 104139. doi: 10.1016/j.apor.2024.104139
[2] GUO Z L, HONG M, ZHANG Y C, et al. Research on safety evaluation and weather routing optimization of ship based on roll dynamics and improved A* algorithm[J]. International Journal of Naval Architecture and Ocean Engineering, 2024, 16: 100605. doi: 10.1016/j.ijnaoe.2024.100605
[3] YANG T Y, WANG X, LIU Z J. A novel ship domain-oriented parameter of ship collision risk considering the ship maneuverability and encounter situation[J]. Journal of Marine Science and Application, 2023, 22(2): 181–198. doi: 10.1007/s11804-023-00330-0
[4] KORUPOJU A K, KAPADIA V, VILWATHILAKAM A S, et al. Ship collision risk evaluation using AIS and weather data through fuzzy logic and deep learning[J]. Ocean Engineering, 2025, 318: 120116. doi: 10.1016/j.oceaneng.2024.120116
[5] 康艺柔, 陈鹏, 程正顺, 等. 人工智能技术在海上风机领域的应用综述[J]. 船舶, 2023, 34(5): 12–23. doi: 10.19423/j.cnki.31-1561/u.2023.05.012 KANG Y R, CHEN P, CHENG Z S, et al. Review of artificial intelligence technology applications in offshore wind turbines[J]. Ship & Boat, 2023, 34(5): 12–23 (in Chinese). doi: 10.19423/j.cnki.31-1561/u.2023.05.012
[6] 张绮轩, 李海锋, 梁远升, 等. 基于行波解析分析的柔性直流输电线路故障智能检测方法[J]. 广东电力, 2024, 37(5): 84–96. doi: 10.3969/j.issn.1007-290X.2024.05.009 ZHANG Q X, LI H F, LIANG Y S, et al. Intelligent fault detection method for flexible DC transmission lines based on prior experience and of travelling wave expression[J]. Guangdong Electric Power, 2024, 37(5): 84–96 (in Chinese). doi: 10.3969/j.issn.1007-290X.2024.05.009
[7] 吴川博, 俞万能. 基于安全等级的动态船舶安全领域模型研究[J]. 中国造船, 2022, 63(6): 218–229. doi: 10.3969/j.issn.1000-4882.2022.06.019 WU C B, YU W N. Research on dynamic ship safety domain model based on safety level[J]. Shipbuilding of China, 2022, 63(6): 218–229 (in Chinese). doi: 10.3969/j.issn.1000-4882.2022.06.019
[8] SUI B W, ZHANG J Q, LIU Z. A real-time ship encounter collision risk detection approach in close-quarters situation[J]. Measurement and Control, 2023, 56(9/10): 1613–1625. doi: 10.1177/00202940231175086
[9] 卢安格, 王子棠, 孔祥韶, 等. 船舶结构碰撞试验及简化数值计算方法[J]. 中国舰船研究, 2024, 19(2): 128–139. doi: 10.19693/j.issn.1673-3185.03193 LU A G, WANG Z T, KONG X S, et al. Ship structure collision experiments and simplified numerical calculation method[J]. Chinese Journal of Ship Research, 2024, 19(2): 128–139 (in Chinese). doi: 10.19693/j.issn.1673-3185.03193
[10] 崔浩, 张新宇, 王警, 等. 自主船舶与有人驾驶船舶动态博弈避碰决策[J]. 中国舰船研究, 2024, 19(1): 238–247. doi: 10.19693/j.issn.1673-3185.03305 CUI H, ZHANG X Y, WANG J, et al. Dynamic game collision avoidance decision-making for autonomous and manned ships[J]. Chinese Journal of Ship Research, 2024, 19(1): 238–247 (in Chinese). doi: 10.19693/j.issn.1673-3185.03305
[11] FENG G X, GU S B, SUN S H. Intelligent ship collision avoidance support system based on the algorithm of anthropomorphic physics[J]. International Journal of Ambient Computing and Intelligence (IJACI), 2024, 15(1): 1–20. doi: 10.4018/IJACI.365340
[12] 孟祥乾, 吴建军, 朱清华, 等. 海上丝绸之路环境影响船舶稳性安全分析方法[J]. 清华大学学报(自然科学版), 2024, 64(6): 1060–1069. doi: 10.16511/j.cnki.qhdxxb.2024.22.017 MENG X Q, WU J J, ZHU Q H, et al. Analytical method to determine the environmental impact on the stability safety of a bulk carrier navigating in the Maritime Silk Road[J]. Journal of Tsinghua University (Science and Technology), 2024, 64(6): 1060–1069 (in Chinese). doi: 10.16511/j.cnki.qhdxxb.2024.22.017
[13] 刘超凡, 郭国平, 吴兵, 等. 基于FAHP-云模型的CAPE型船舶内河航行安全评估[J]. 武汉理工大学学报, 2021, 43(7): 29–35,47. LIU C F, GUO G P, WU B, et al. CAPE-type ship navigation safety assessment based on FAHP-cloud model[J]. Journal of Wuhan University of Technology, 2021, 43(7): 29–35,47 (in Chinese).
[14] 冯珂, 张本伟. 复杂气象海况条件下船舶航行安全辨识及航行优化方法[J]. 中国航海, 2022, 45(3): 1–6. doi: 10.3969/j.issn.1000-4653.2022.03.001 FENG K, ZHANG B W. Ship navigation safety identification and optimization under complex sea and weather conditions[J]. Navigation of China, 2022, 45(3): 1–6 (in Chinese). doi: 10.3969/j.issn.1000-4653.2022.03.001
[15] 杨家轩, 许洲锦, 来源, 等. 基于概率攻击图的船舶网络安全评估模型[J]. 大连海事大学学报, 2023, 49(1): 26–33. doi: 10.16411/j.cnki.issn1006-7736.2023.01.003 YANG J X, XU Z J, LAI Y, et al. Ship cyber security assessment model based on probability attack graph[J]. Journal of Dalian Maritime University, 2023, 49(1): 26–33 (in Chinese). doi: 10.16411/j.cnki.issn1006-7736.2023.01.003
[16] ZHOU H Z, YU G, LI L G. Cloud communication based ship communication network security risk assessment model[J]. Journal of Coastal Research, 2020, 95(sp1): 991–995. doi: 10.2112/SI95-193.1
[17] 徐湃. 基于人工智能技术的船舶网络安全控制系统[J]. 舰船科学技术, 2023, 45(3): 153–156. doi: 10.3404/j.issn.1672-7649.2023.03.029 XU P. Research on ship network security control system based on artificial intelligence technology[J]. Ship Science and Technology, 2023, 45(3): 153–156 (in Chinese). doi: 10.3404/j.issn.1672-7649.2023.03.029
[18] 蒋欣秀, 常俊, 李波, 等. 面向海洋节能边缘计算的任务卸载研究[J]. 计算机工程与科学, 2022, 44(9): 1563–1573. doi: 10.3969/j.issn.1007-130X.2022.09.006 JIANG X X, CHANG J, LI B, et al. Research on task unloading for marine energy-saving edge computing[J]. Computer Engineering & Science, 2022, 44(9): 1563–1573 (in Chinese). doi: 10.3969/j.issn.1007-130X.2022.09.006
[19] SONG F F, ZHU J, GUO S Y. Research on information security protected scheme for ship network system[J]. IOP Conference Series: Materials Science and Engineering, 2019, 631(5): 052051. doi: 10.1088/1757-899X/631/5/052051
[20] 丁可, 徐言民, 关宏旭, 等. 基于贪心−遗传优化算法的中长期船舶进出港调度优化[J]. 武汉理工大学学报(交通科学与工程版), 2023, 47(4): 770–774. doi: 10.3963/j.issn.2095-3844.2023.04.035 DING K, XU Y M, GUAN H X, et al. Medium-and long-term ship entry and exit scheduling optimization based on greedy-genetic optimization algorithm[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2023, 47(4): 770–774 (in Chinese). doi: 10.3963/j.issn.2095-3844.2023.04.035
[21] 李润佛, 张新宇, 李俊杰, 等. 基于强化学习的自学习遗传算法在船舶调度中的应用[J]. 大连海事大学学报, 2022, 48(3): 20–30. doi: 10.16411/j.cnki.issn1006-7736.2022.03.003 LI R F, ZHANG X Y, LI J J, et al. Application of self-learning genetic algorithm based on reinforcement learning in ship scheduling[J]. Journal of Dalian Maritime University, 2022, 48(3): 20–30 (in Chinese). doi: 10.16411/j.cnki.issn1006-7736.2022.03.003
[22] 范厚明, 于佳琪, 马梦知, 等. 模糊时间窗下多船型不定期船调度与航速联合优化[J]. 上海交通大学学报, 2021, 55(3): 297–310. doi: 10.16183/j.cnki.jsjtu.2019.215 FAN H M, YU J Q, MA M Z, et al. Heterogeneous tramp ship scheduling and speed optimization with fuzzy time window[J]. Journal of Shanghai Jiaotong University, 2021, 55(3): 297–310 (in Chinese). doi: 10.16183/j.cnki.jsjtu.2019.215
[23] LI R F, ZHANG X Y, WANG C B, et al. A machine learning-based adaptive heuristic for vessel scheduling problem under uncertainty via chance-constrained programming[J]. Computers and Electrical Engineering, 2024, 119: 109523. doi: 10.1016/j.compeleceng.2024.109523
[24] LIU S, ZHANG Y, GUO W J, et al. Ship appointment scheduling for lockage operations of waterway transport with non-punctual arrivals[J]. Ocean Engineering, 2025, 315: 119844. doi: 10.1016/j.oceaneng.2024.119844
[25] ZHOU M J, CAO L, LIU J H, et al. Research on intelligent three-dimensional anchor position detection method for ships utilizing Traversal and Monte Carlo algorithms[J]. Frontiers in Marine Science, 2024, 11: 1471328. doi: 10.3389/fmars.2024.1471328
[26] CUI Z K, ZHANG X L, CHEN Y L, et al. Intelligent detection of 3D anchor position based on Monte Carlo algorithm[J]. Journal of Marine Science and Engineering, 2024, 12(8): 1347. doi: 10.3390/jmse12081347
[27] WNOROWSKI J, ŁEBKOWSKI A. Verification of the system for ship position keeping equipped with a set of anchors in Unity3d[J]. Sensors, 2022, 22(19): 7421. doi: 10.3390/s22197421
[28] 刘建, 唐瑜. 项目级施工船舶管理平台的研究与应用[J]. 中国港湾建设, 2022, 42(12): 80–84. doi: 10.7640/ZGGWJS202212017 LIU J, TANG Y. Research and application of working vessel management platform at project level[J]. China Harbour Engineering, 2022, 42(12): 80–84 (in Chinese). doi: 10.7640/ZGGWJS202212017
[29] WU C, WANG S G, LONG J J, et al. Research on modular design and manufacturing of ship anchor winch structure under artificial intelligence optimisation[J]. International Journal of Wireless and Mobile Computing, 2022, 22(2): 148–156. doi: 10.1504/IJWMC.2022.123315
[30] LEE S W, SASA K, CHEN C, et al. Novel safety evaluation technique for ships in offshore anchorage under rough seas conditions for optimal ship routing[J]. Ocean Engineering, 2022, 253: 111323. doi: 10.1016/j.oceaneng.2022.111323
[31] SUN Q, LIU J M, ZHOU H. Analysis on towing damage and protection suggestions of submarine pipelines caused by ship anchoring operation[J]. Journal of Physics: Conference Series, 2024, 2913: 012007. doi: 10.1088/1742-6596/2913/1/012007
[32] 李雪剑, 秦斌, 肖艺峰, 等. 改进随机森林−蒙特卡罗法在A型液舱支座结构可靠性分析中的应用[J]. 中国舰船研究, 2022, 17(1): 147–153,165. doi: 10.19693/j.issn.1673-3185.02181 LI X J, QIN B, XIAO Y F, et al. An improved random forest-Monte Carlo method and application for structural reliability analysis of A-type independent liquid tank support structure[J]. Chinese Journal of Ship Research, 2022, 17(1): 147–153,165 (in Chinese). doi: 10.19693/j.issn.1673-3185.02181
[33] JI F R, LIU B L. A systematic network pruning framework using ADMM-type algorithm[J]. Multimedia Systems, 2024, 30(6): 373. doi: 10.1007/s00530-024-01571-x
[34] 王鹏, 张嘉诚, 范毓洋. 适应于硬件部署的神经网络剪枝量化算法[J]. 计算机工程与科学, 2024, 46(9): 1547–1553. doi: 10.3969/j.issn.1007-130X.2024.09.004 WANG P, ZHANG J C, FAN Y Y. A neural network pruning and quantization algorithm for hardware deployment[J]. Computer Engineering & Science, 2024, 46(9): 1547–1553 (in Chinese). doi: 10.3969/j.issn.1007-130X.2024.09.004
[35] 罕天玺, 杨锐良, 李正志, 等. 姿态传感与神经网络融合的验电行为检测方法[J]. 广东电力, 2024, 37(8): 101–108. doi: 10.3969/j.issn.1007-290X.2024.08.011 HAN T X, YANG R L, LI Z Z, et al. Behavior detection of electricity testing based on BP network and attitude sensor[J]. Guangdong Electric Power, 2024, 37(8): 101–108 (in Chinese). doi: 10.3969/j.issn.1007-290X.2024.08.011
[36] 邹俊杰. 抗随机干扰的船舶动力系统混合控制方法[J]. 舰船科学技术, 2022, 44(22): 106–109. doi: 10.3404/j.issn.1672-7649.2022.22.019 ZOU J J. Hybrid control method for ship power system against random disturbance[J]. Ship Science and Technology, 2022, 44(22): 106–109 (in Chinese). doi: 10.3404/j.issn.1672-7649.2022.22.019
计量
- 文章访问数: 47
- HTML全文浏览量: 5
- PDF下载量: 0
