Time-domain shielding effectiveness analysis based on DGTD method
-
摘要:目的 为精确分析金属屏蔽腔的时域屏蔽效能，提出一种基于局部时间步进技术和并行技术的时域不连续伽辽金（DGTD）算法。方法 利用DGTD算法，对金属屏蔽腔进行全波电磁仿真，进而计算时域屏蔽效能（TDSE）；利用局部时间步进（LTS）技术增大时间步长，然后结合并行技术显著缩短计算时间；分析金属屏蔽腔的孔径尺寸、腔体厚度、阵列孔间距等设计参数对时域屏蔽效能的影响。结果 数值算例结果显示，所提方法正确、有效。结论 所提方法为电磁屏蔽问题的仿真提供了一种有效的工具，对金属屏蔽腔的设计具有一定的指导意义。
-
关键词:
- 金属屏蔽腔 /
- 时域屏蔽效能 /
- 时域不连续伽辽金算法 /
- 局部时间步进 /
- 并行技术
Abstract:Objective In order to accurately analyze the time-domain shielding effectiveness (TDSE) of metallic enclosures, a discontinuous Galerkin time domain (DGTD) method based on the local time-stepping (LTS) technique and parallel technique is proposed.Methods The full wave electromagnetic simulation of metallic enclosures is carried out by the DGTD method, and the TDSE is then calculated. LTS technology is used to increase the time step size, combined with parallel technology to greatly shorten the computing time. The influence of design parameters such as aperture size, enclosure thickness and array hole spacing on TDSE is then analyzed.Results The numerical results show that the proposed method is correct and effective.Conclusion The proposed method provides an effective tool for the simulation of electromagnetic shielding problems, and has certain guiding significance for the design of metallic enclosures. -
0. 引 言
随着电子信息技术的飞速发展，各种电子设备在民用和军事领域均得到了广泛应用。这些电子设备通常对电磁干扰（electromagnetic interference，EMI）很敏感。典型的电磁干扰源主要包括民用领域的各种无线设备、电气设备、高速数字电子设备，以及军用领域[1]的雷达、高功率微波（high power microwave，HPM）、强电磁脉冲（electromagnetic pulse，EMP）等。设计电磁屏蔽是提高电子设备抗电磁干扰能力的有效手段，通常将屏蔽效能（shielding effectiveness，SE）作为衡量金属屏蔽腔[2]抗电磁干扰能力的技术指标。
屏蔽腔的屏蔽效能通常是在设计阶段通过解析方法或是数值模拟得到的。运用解析方法虽然简单、快速，但仅适用于长方体、圆柱体等规则的屏蔽腔结构，当屏蔽腔结构不规则时，难以应用[3-7]。近年来，数值模拟方法因为其通用性和精度受到许多研究人员的青睐。常用的数值模拟方法有时域有限差分法（finite difference time-domain，FDTD）[8-12]、有限元法（finite element method，FEM）[13-14]和矩量法（method of moments，MoM）[15-19]。例如，Liu等[12]采用FDTD法研究了电磁屏蔽织物的屏蔽效能。Feliziani[13]基于FEM研究了屏蔽电缆与电磁场的耦合效应。Nazari等[16]改进了MoM，并采用此方法模拟了雷电作用于金属屏蔽腔的场景。
上述文献主要是针对传统频域屏蔽效能的数值模拟。如果采用FDTD法等时域数值方法研究频域屏蔽效能，则需要将仿真得到的瞬态场进行傅里叶变换，然后再计算得到宽带的屏蔽效能[10]；如果采用FEM和MoM等频域数值方法，则一次可以计算一个频率点的屏蔽效能。然而，传统的频域屏蔽效能本质上仅适用于谐波激励。当激励为瞬态的EMP信号时，传统的频域屏蔽效能不能很好地量化屏蔽腔的电磁屏蔽效果。因此，Araneo等[20] 和Celozzi等[21] 定义了时域屏蔽效能（time-domain shielding effectiveness，TDSE），用于衡量屏蔽腔的时域电磁屏蔽能力。由于TDSE是直接在时域上根据瞬态电磁场进行定义，因此通常采用时域数值方法[22-23]分析TDSE。经典的FDTD方法要求使用正交网格进行网格划分，但当模型具有曲面结构时，会产生阶梯效应。时域不连续伽辽金（discontinuous Galerkin time domain，DGTD）算法是近年来提出的一种类似于时域有限元（time- domain finite element，FETD）法[24-26]的方法，它可以利用四面体单元对任意形状的几何模型进行精确的网格剖分。采用DGTD算法只需求解与每个四面体单元相关的局部矩阵方程即可，而若采用FETD法，则需要求解与所有单元相关的全局大矩阵方程。因此，在计算资源有限的情况下，采用DGTD算法求解大规模的问题其能力要优于FETD法。
由于屏蔽腔通常含有孔缝等精细结构，导致屏蔽腔成为多尺度结构，而DGTD算法为显式算法，其时间步长受剖分生成的最小网格尺寸约束，因此直接采用DGTD算法分析屏蔽腔其时间步长较小，仿真效率较低。为此，本文拟将局部时间步进（local time-stepping，LTS）和并行技术引入DGTD算法中，通过LTS技术增加大尺度区域的时间步长，然后采用METIS软件对网格进行均匀分组，以保证负载均衡，减少不同进程之间的通信，从而有效提高对屏蔽腔问题的仿真速度。最后，分析屏蔽腔的孔径尺寸、腔体厚度、阵列孔间距等设计参数对TDSE的影响，总结出一些能有效提高TDSE的设计规律。
1. 理论与公式
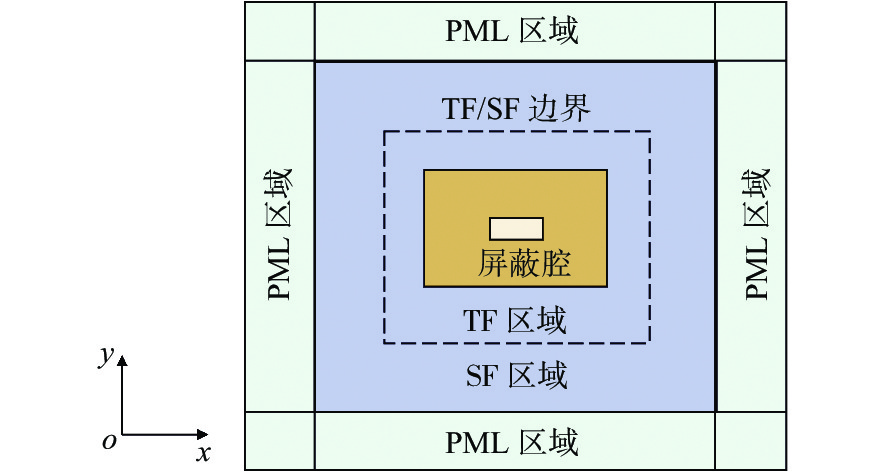
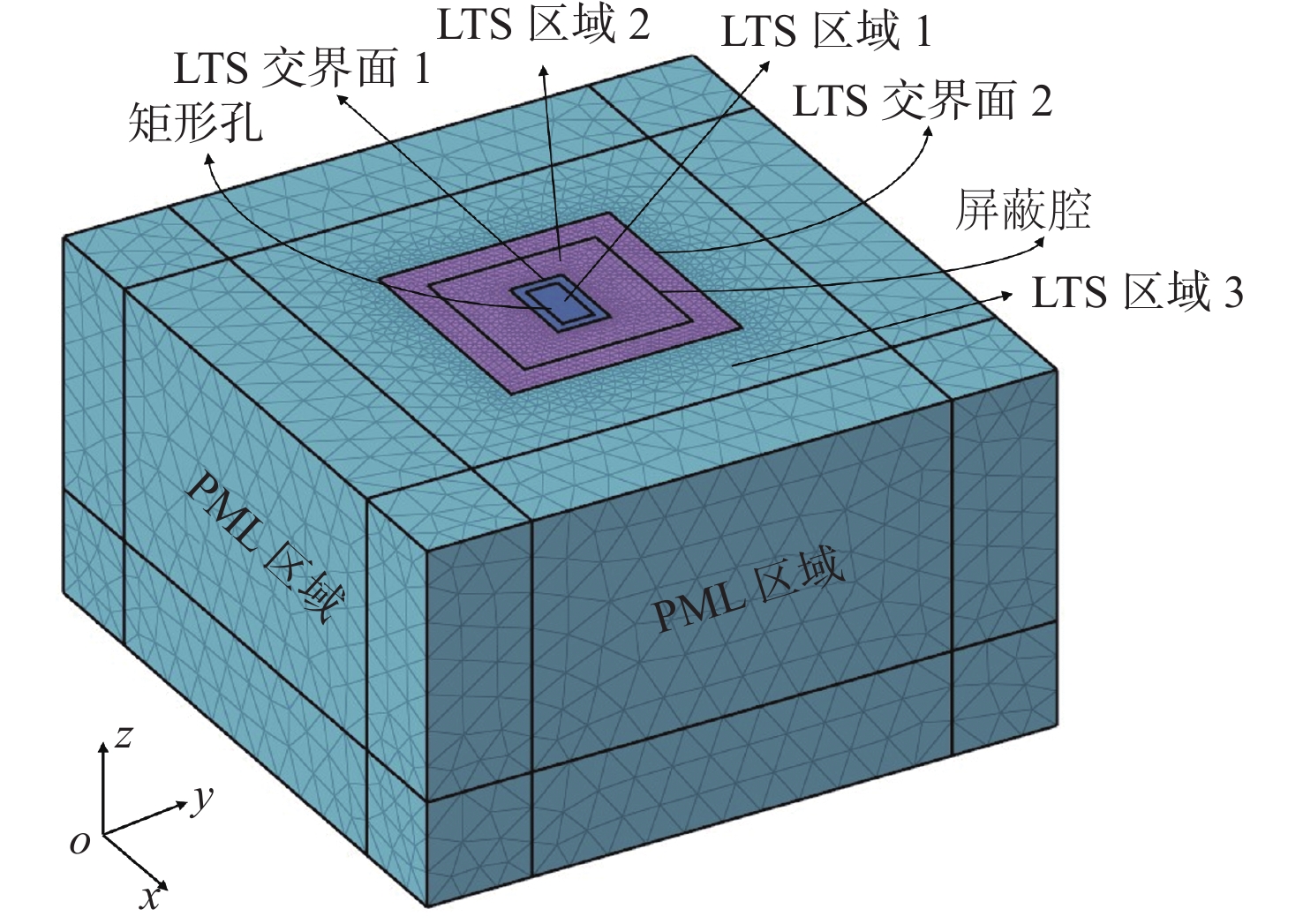
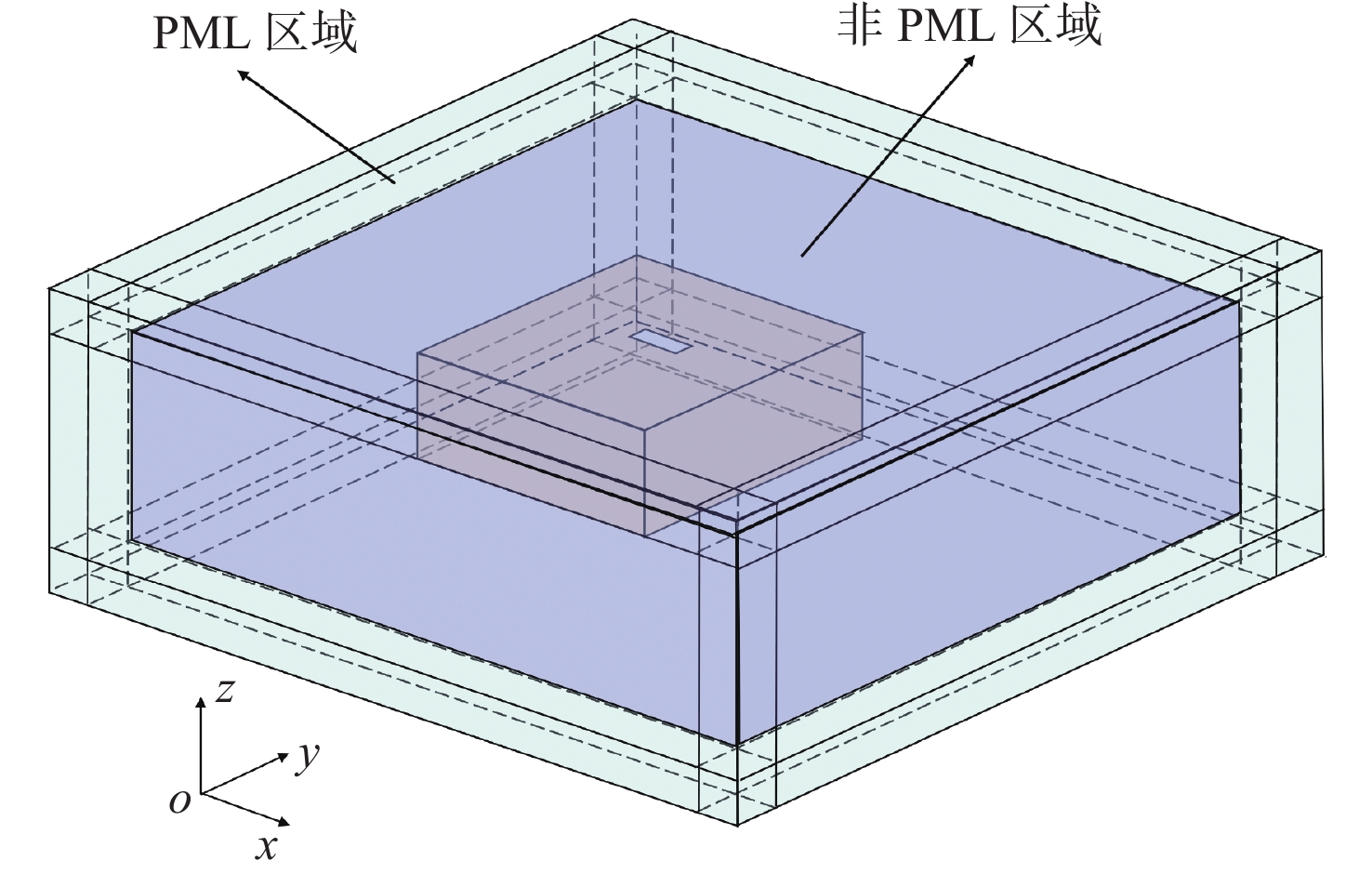
在分析电磁屏蔽问题时，因入射波照射金属屏蔽腔后会散射至整个自由空间，而计算区域又不可能无限大，因此，就需要一个吸收边界条件来截断DGTD计算域。本文选择单轴各向异性完美匹配层（uniaxial anisotropic perfectly matched layer，UPML）作为吸收边界条件[27]。于是，整个计算域被划分为2个区域（图1）：PML区域和非PML区域。本节将针对非PML区域的DGTD和PML区域的DGTD算法，以及LTS方法和并行策略这4个部分予以详细介绍。
![]()
图 1 金属屏蔽体屏蔽效能分析的三维计算域Figure 1. The 3-D computational domain for the shielding effectiveness analysis of metallic enclosure1.1 非PML区域的DGTD算法
DGTD算法从麦克斯韦方程组出发：
\varepsilon \frac{{\partial {\boldsymbol{E}}}}{{\partial t}} = \nabla \times {\boldsymbol{H}} (1) \mu \frac{{\partial {\boldsymbol{H}}}}{{\partial t}} = - \nabla \times {\boldsymbol{E}} (2) 式中：E为电场强度；H为磁场强度； \varepsilon 为介电常数； \mu 为磁导率；t为时间变量； \nabla 为矢量微分算子。
在进行网格剖分时，非PML区域被划分为N个四面体单元 {V_1} ， {V_2} ,…, {V_N} ，其中第i个单元的的表面用 \partial {V_i} 表示。对式（1）和式（2）进行伽辽金法测试，可得
\int_{{V_i}} {\varepsilon {{\boldsymbol{N}}_k} \cdot \frac{{\partial {\boldsymbol{E}}}}{{\partial t}}{\rm{d}}V} = \int_{{V_i}} {\nabla \times {{\boldsymbol{N}}_k} \cdot {\boldsymbol{H}}{\rm{d}}V} + \int_{\partial {V_i}} {{{\boldsymbol{N}}_k} \cdot \hat {\boldsymbol{n}} \times {\boldsymbol{H}}{\rm{d}}S} (3) \int_{{V_i}} {\mu {{\boldsymbol{N}}_k} \cdot \frac{{\partial {\boldsymbol{H}}}}{{\partial t}}{\rm{d}}V} = - \int_{{V_i}} {\nabla \times {{\boldsymbol{N}}_k} \cdot {\boldsymbol{E}}{\rm{d}}V} - \int_{\partial {V_i}} {{{\boldsymbol{N}}_k} \cdot \hat {\boldsymbol{n}} \times {\boldsymbol{E}}{\rm{d}}S} (4) 式中：{{\boldsymbol{N}}}_{k}\left(k=1,\;2,...,20\right)为二阶的矢量叠层基函数[28-29]； \hat {\boldsymbol{n}} 为单元面的单位法矢量；S为单元的面。
迎风数值通量表达式为：
\begin{split} & \hat {\boldsymbol{n}} \times {\boldsymbol{H}} = \hat {\boldsymbol{n}} \times {{\boldsymbol{H}}^i} + \frac{{{Z^j}}}{{{Z^i} + {Z^j}}}\hat {\boldsymbol{n}} \times ({{\boldsymbol{H}}^j} - {{\boldsymbol{H}}^i}) + \\&\qquad\;\;\; \frac{1}{{{Z^i} + {Z^j}}}\hat {\boldsymbol{n}} \times (\hat {\boldsymbol{n}} \times ({{\boldsymbol{E}}^i} - {{\boldsymbol{E}}^j})) \end{split} (5) \begin{split} & \hat {\boldsymbol{n}} \times {\boldsymbol{E}} = \hat {\boldsymbol{n}} \times {{\boldsymbol{E}}^i} + \frac{{{Y^j}}}{{{Y^i} + {Y^j}}}\hat {\boldsymbol{n}} \times ({{\boldsymbol{E}}^j} - {{\boldsymbol{E}}^i}) + \\&\qquad\;\;\;\; \frac{1}{{{Y^i} + {Y^j}}}\hat {\boldsymbol{n}} \times (\hat {\boldsymbol{n}} \times ({{\boldsymbol{H}}^j} - {{\boldsymbol{H}}^i})) \end{split} (6) 式中， {Z^i} = 1/{Y^i} = \sqrt {{\mu ^i}/{\varepsilon ^i}} ， {Z^j} = 1/{Y^j} = \sqrt {{\mu ^j}/{\varepsilon ^j}} ，分别为第i个单元和相邻第j个单元的波阻抗，其中 {Y^i} 和 {Y^j} 分别为第i个单元和相邻第j个单元的波导纳。
将迎风数值通量代入式（3）和式（4）中的面积分项并进行基函数展开，得到空间离散化矩阵方程为
\varepsilon {{\boldsymbol{M}}^i}\frac{{\partial {{\boldsymbol{e}}^i}}}{{\partial t}} = {\text{ }}{{\boldsymbol{S}}^i}{{\boldsymbol{h}}^i}{\text{ + }}{\boldsymbol{F}}_{ee}^{ii}{{\boldsymbol{e}}^i} - {\boldsymbol{F}}_{ee}^{ij}{{\boldsymbol{e}}^j} - {\boldsymbol{F}}_{eh}^{ii}{{\boldsymbol{h}}^i} + {\boldsymbol{F}}_{eh}^{ij}{{\boldsymbol{h}}^j} (7) \mu {{\boldsymbol{M}}^i}\frac{{\partial {{\boldsymbol{h}}^i}}}{{\partial t}} = {\text{ }} - {{\boldsymbol{S}}^i}{{\boldsymbol{e}}^i} + {\boldsymbol{F}}_{hh}^{ii}{{\boldsymbol{h}}^i} - {\boldsymbol{F}}_{hh}^{ij}{{\boldsymbol{h}}^j} + {\boldsymbol{F}}_{he}^{ii}{{\boldsymbol{e}}^i} - {\boldsymbol{F}}_{he}^{ij}{{\boldsymbol{e}}^j} (8) 式中， {{\boldsymbol{h}}^i} ， {{\boldsymbol{h}}^j} 和 {{\boldsymbol{e}}^i} ， {{\boldsymbol{e}}^j} 分别为磁声耦合系数矩阵与电场耦合系数矩阵，其他矩阵元素的表达式如下：
{[ {{{\boldsymbol{M}}^i}} ]_{kl}} = \int_{{V_i}} {{\boldsymbol{N}}_k^i \cdot {\boldsymbol{N}}_l^i{\rm{d}}V} {[ {{{\boldsymbol{S}}^i}} ]_{kl}} = \int_{{V_i}} {{\boldsymbol{N}}_k^i \cdot (\nabla \times {\boldsymbol{N}}_l^i){\rm{d}}V} {[ {{\boldsymbol{F}}_{ee}^{ii}} ]_{kl}}{\text{ = }}\frac{1}{{{Z^i} + {Z^j}}}\int_{\partial {V_i}} {{\boldsymbol{N}}_k^i \cdot (\hat {\boldsymbol{n}} \times \hat {\boldsymbol{n}} \times {\boldsymbol{N}}_l^i){\rm{d}}S} {[ {{\boldsymbol{F}}_{ee}^{ij}} ]_{kl}}{\text{ = }}\frac{1}{{{Z^i} + {Z^j}}}\int_{\partial {V_i}} {{\boldsymbol{N}}_k^i \cdot (\hat {\boldsymbol{n}} \times \hat {\boldsymbol{n}} \times {\boldsymbol{N}}_l^j){\rm{d}}S} {[ {{\boldsymbol{F}}_{eh}^{ii}} ]_{kl}}{\text{ = }}\frac{{{Z^j}}}{{{Z^i} + {Z^j}}}\int_{\partial {V_i}} {{\boldsymbol{N}}_k^i \cdot (\hat {\boldsymbol{n}} \times {\boldsymbol{N}}_l^i){\rm{d}}S} {[ {{\boldsymbol{F}}_{eh}^{ij}} ]_{kl}}{\text{ = }}\frac{{{Z^j}}}{{{Z^i} + {Z^j}}}\int_{\partial {V_i}} {{\boldsymbol{N}}_k^i \cdot (\hat {\boldsymbol{n}} \times {\boldsymbol{N}}_l^j){\rm{d}}S} {[ {{\boldsymbol{F}}_{he}^{ii}} ]_{kl}}{\text{ = }}\frac{{{Y^j}}}{{{Y^i} + {Y^j}}}\int_{\partial {V_i}} {{\boldsymbol{N}}_k^i \cdot (\hat {\boldsymbol{n}} \times {\boldsymbol{N}}_l^i){\rm{d}}S} {[ {{\boldsymbol{F}}_{he}^{ij}} ]_{kl}}{\text{ = }}\frac{{{Y^j}}}{{{Y^i} + {Y^j}}}\int_{\partial {V_i}} {{\boldsymbol{N}}_k^i \cdot (\hat {\boldsymbol{n}} \times {\boldsymbol{N}}_l^j){\rm{d}}S} {[ {{\boldsymbol{F}}_{hh}^{ii}} ]_{kl}}{\text{ = }}\frac{1}{{{Y^i} + {Y^j}}}\int_{\partial {V_i}} {{\boldsymbol{N}}_k^i \cdot (\hat {\boldsymbol{n}} \times \hat {\boldsymbol{n}} \times {\boldsymbol{N}}_l^i){\rm{d}}S} {[ {{\boldsymbol{F}}_{hh}^{ij}} ]_{kl}}{\text{ = }}\frac{1}{{{Y^i} + {Y^j}}}\int_{\partial {V_i}} {{\boldsymbol{N}}_k^i \cdot (\hat {\boldsymbol{n}} \times \hat {\boldsymbol{n}} \times {\boldsymbol{N}}_l^j){\rm{d}}S} 式中， {\boldsymbol{N}}_l^i ， {\boldsymbol{N}}_l^j， {\boldsymbol{N}}_k^i 表示基函数。采用蛙跳格式对式（7）和式（8）进行时间离散，可得到最终完全离散的矩阵方程为：
\begin{split} & \varepsilon {{\boldsymbol{M}}^i}{\boldsymbol{e}}_{n + 1}^i = {\text{ }}\varepsilon {{\boldsymbol{M}}^i}{\boldsymbol{e}}_n^i + \Delta t[{{\boldsymbol{S}}^i}{\boldsymbol{h}}_{n + 1/2}^i + {\boldsymbol{F}}_{ee}^{ii}{\boldsymbol{e}}_n^i -\\&\qquad {\boldsymbol{F}}_{ee}^{ij}{\boldsymbol{e}}_n^j - {\boldsymbol{F}}_{eh}^{ii}{\boldsymbol{h}}_{n + 1/2}^i + {\boldsymbol{F}}_{eh}^{ij}{\boldsymbol{h}}_{n + 1/2}^j] \end{split} (9) \begin{split} & \mu {{\boldsymbol{M}}^i}{\boldsymbol{h}}_{n + 3/2}^i = \mu {{\boldsymbol{M}}^i}{\boldsymbol{h}}_{n + 1/2}^i + \Delta t[ - {{\boldsymbol{S}}^i}{\boldsymbol{e}}_{n + 1}^i + {\boldsymbol{F}}_{hh}^{ii}{\boldsymbol{h}}_{n + 1/2}^i - \\&\qquad\qquad {\boldsymbol{F}}_{hh}^{ij}{\boldsymbol{h}}_{n + 1/2}^j + {\boldsymbol{F}}_{he}^{ii}{\boldsymbol{e}}_{n + 1}^i - {\boldsymbol{F}}_{he}^{ij}{\boldsymbol{e}}_{n + 1}^j] \end{split} (10) 式中，n为时刻。
如图2所示，非PML区域由总场（total field，TF）区域和散射场（scattering field，SF）区域组成，其中入射波的电场强度 {{\boldsymbol{E}}^{\rm{inc}}} 和磁场强度 {{\boldsymbol{H}}^{\rm{inc}}} 只存在于TF区。通过修改数值通量来施加入射波，当TF/SF交界面上的单元位于TF区域时，数值通量需要修改为：
![]()
图 2 金属屏蔽体屏蔽效能分析的二维计算域Figure 2. The 2-D computational domain for the shielding effectiveness analysis of metallic enclosure\hat {\boldsymbol{n}} \times {{\boldsymbol{E}}^j} = \hat {\boldsymbol{n}} \times ({{\boldsymbol{E}}^j} + {{\boldsymbol{E}}^{\rm{inc}}}) (11) \hat {\boldsymbol{n}} \times {{\boldsymbol{H}}^j} = \hat {\boldsymbol{n}} \times ({{\boldsymbol{H}}^j} + {{\boldsymbol{H}}^{\rm{inc}}}) (12) 当TF/SF界面上的单元位于SF区域时，数值通量需要修改为：
\hat {\boldsymbol{n}} \times {{\boldsymbol{E}}^j} = \hat {\boldsymbol{n}} \times ({{\boldsymbol{E}}^j} - {{\boldsymbol{E}}^{\rm{inc}}}) (13) \hat {\boldsymbol{n}} \times {{\boldsymbol{H}}^j} = \hat {\boldsymbol{n}} \times ({{\boldsymbol{H}}^j} - {{\boldsymbol{H}}^{\rm{inc}}}) (14) 1.2 PML区域的DGTD算法
PML区域的控制方程包括麦克斯韦方程组和2个辅助方程[30]：
\varepsilon \bar {\bar {\boldsymbol{a}}} \cdot \frac{{\partial {\boldsymbol{E}}}}{{\partial t}} = - \varepsilon \bar {\bar {\boldsymbol{b}}} \cdot {\boldsymbol{E}} - \varepsilon \bar {\bar {\boldsymbol{c}} }\cdot {{\boldsymbol{p}}^e} + \nabla \times {\boldsymbol{H}} (15) \frac{{\partial {{\boldsymbol{p}}^h}}}{{\partial t}} = {\bar {\bar {\boldsymbol{k}}}^{ - 1}} \cdot {\boldsymbol{H}} - \bar{ \bar {\boldsymbol{d}}} \cdot {{\boldsymbol{p}}^h} (16) \mu \bar {\bar {\boldsymbol{a}} }\cdot \frac{{\partial {\boldsymbol{H}}}}{{\partial t}} = - \mu \bar {\bar {\boldsymbol{b}}} \cdot {\boldsymbol{H}} - \mu \bar {\bar {\boldsymbol{c}}} \cdot {{\boldsymbol{p}}^h} - \nabla \times {\boldsymbol{E}} (17) \frac{{\partial {{\boldsymbol{p}}^e}}}{{\partial t}} = {{\bar {\bar {\boldsymbol{k}}}}^{ - 1}} \cdot {\boldsymbol{E}} - {\bar {\bar {\boldsymbol{d}}}} \cdot {{\boldsymbol{p}}^e} (18) 式中： {{\boldsymbol{p}}^e} 和 {{\boldsymbol{p}}^h} 为辅助变量； {\bar {\bar {\boldsymbol{a}}}} ， {\bar {\bar {\boldsymbol{b}}}} ， {\bar {\bar {\boldsymbol{c}}}} ， {\bar {\bar {\boldsymbol{d}}}} ， {\bar {\bar {\boldsymbol{k}}}} 为对角张量，它们的第1个元素可以表示为：
\begin{split} & {a_{xx}} = \frac{{{\kappa _y}{\kappa _{\textit{z}}}}}{{{\kappa _x}}},\;\;\;{b_{xx}} = \frac{{({\sigma _y}{\kappa _{\textit{z}}} + {\sigma _{\textit{z}}}{\kappa _y} - {a_{xx}}{\sigma _x})}}{{{\kappa _x}{\varepsilon ^{}}}} \\& {c_{xx}} = \frac{{{\sigma _y}{\sigma _{\textit{z}}}}}{{{\varepsilon ^2}}} - {b_{xx}}\frac{{{\sigma _x}}}{{{\varepsilon ^{}}}},\;\;\;{d_{xx}} = \frac{{{\sigma _x}}}{{{\kappa _x}\varepsilon }},\;\;\;{k_{xx}} = {\kappa _x} \end{split} (19) 以上对角张量中其余元素的表达式可以通过对式（19）中下标的简单递推得到。 {\kappa _i} 和 {\sigma _i} 是PML矩阵相关的参数，其取值与Gedney[31]给出的取值一致。在非PML区域采用类似的推导方法，可得到空间离散后的PML区域矩阵方程为：
\begin{split} & \varepsilon {\boldsymbol{T}}_a^i\frac{{\partial {{\boldsymbol{e}}^i}}}{{\partial t}} = {\text{ }} - \varepsilon {\boldsymbol{T}}_b^i{{\boldsymbol{e}}^i} - \varepsilon {\boldsymbol{T}}_c^i{{\boldsymbol{p}}^e} + {{\boldsymbol{S}}^i}{{\boldsymbol{h}}^i} -\\&\;\;\;\; {\boldsymbol{F}}_{eh}^{ii}{{\boldsymbol{h}}^i} + {\boldsymbol{F}}_{ee}^{ii}{{\boldsymbol{e}}^i} + {\boldsymbol{F}}_{eh}^{ij}{{\boldsymbol{h}}^j} - {\boldsymbol{F}}_{ee}^{ij}{{\boldsymbol{e}}^j} \end{split} (20) {{\boldsymbol{M}}^i}\frac{{\partial {{\boldsymbol{p}}^h}}}{{\partial t}} = {\boldsymbol{T}}_k^i{h^i} - {\boldsymbol{T}}_d^i{{\boldsymbol{p}}^h} (21) \begin{split} & \mu {\boldsymbol{T}}_a^i\frac{{\partial {{\boldsymbol{h}}^i}}}{{\partial t}} = {\text{ }} - \mu {\boldsymbol{T}}_b^i{{\boldsymbol{h}}^i} - \mu {\boldsymbol{T}}_c^i{{\boldsymbol{p}}^h} - {{\boldsymbol{S}}^i}{{\boldsymbol{e}}^i} + {\boldsymbol{F}}_{he}^{ii}{{\boldsymbol{e}}^i} +\\&\qquad\qquad {\boldsymbol{F}}_{hh}^{ii}{{\boldsymbol{h}}^i} - {\boldsymbol{F}}_{he}^{ii}{{\boldsymbol{e}}^j} - {\boldsymbol{F}}_{hh}^{ij}{{\boldsymbol{h}}^j} \end{split} (22) {\boldsymbol{M}}^i\frac{{\partial {{\boldsymbol{p}}^e}}}{{\partial t}} = {\boldsymbol{T}}_k^i{{\boldsymbol{e}}^i} - {\boldsymbol{T}}_d^i{{\boldsymbol{p}}^e} (23) 其中：
{\left[ {{\boldsymbol{T}}_a^i} \right]_{kl}} = \int_{{V_i}} {{\boldsymbol{N}}_k^i \cdot {\bar {\bar {\boldsymbol{a}}}} \cdot {\boldsymbol{N}}_l^i} {\rm{d}}V {\left[ {{\boldsymbol{T}}_b^i} \right]_{kl}} = \int_{{V_i}} {{\boldsymbol{N}}_k^i \cdot {\bar {\bar {\boldsymbol{b}}}} \cdot {\boldsymbol{N}}_l^i} {\rm{d}}V {\left[ {{\boldsymbol{T}}_c^i} \right]_{kl}} = \int_{{V_i}} {{\boldsymbol{N}}_k^i \cdot {\bar {\bar {\boldsymbol{c}}}} \cdot {\boldsymbol{N}}_l^i} {\rm{d}}V {\left[ {{\boldsymbol{T}}_d^i} \right]_{kl}} = \int_{{V_i}} {{\boldsymbol{N}}_k^i \cdot {\bar {\bar {\boldsymbol{d}}}} \cdot {\boldsymbol{N}}_l^i} {\rm{d}}V {\left[ {{\boldsymbol{T}}_k^i} \right]_{kl}} = \int_{{V_i}} {{\boldsymbol{N}}_k^i \cdot {{{\bar {\bar {\boldsymbol{k}}}}}^{ - 1}} \cdot {\boldsymbol{N}}_l^i} {\rm{d}}V 然后，对式（20）～式（23）进行时间离散，得到PML区域完全离散的矩阵方程为 ：
\begin{split} & \left(\varepsilon {\boldsymbol{T}}_a^i + \frac{{\Delta t}}{2}\varepsilon {\boldsymbol{T}}_b^i\right){\boldsymbol{e}}_{n + 1}^i = \left( {\varepsilon {\boldsymbol{T}}_a^i - \frac{{\Delta t}}{2}\varepsilon {\boldsymbol{T}}_b^i} \right){\boldsymbol{e}}_n^i + \\&\quad \Delta t[ - \varepsilon {\boldsymbol{T}}_c^i{\boldsymbol{p}}_{n + 1/2}^e + ({{\boldsymbol{S}}^i} - {\boldsymbol{F}}_{eh}^{ii}){\boldsymbol{h}}_{n + 1/2}^i +\\&\quad\qquad {\boldsymbol{F}}_{eh}^{ij}{\boldsymbol{h}}_{n + 1/2}^j + {\boldsymbol{F}}_{ee}^{ii}{\boldsymbol{e}}_n^i - {\boldsymbol{F}}_{ee}^{ij}{\boldsymbol{e}}_n^j] \end{split} (24) \left({\boldsymbol{M}}^i + \frac{{\Delta t}}{2}{\boldsymbol{T}}_d^i\right){\boldsymbol{p}}_{n + 1}^h = \Delta t{\boldsymbol{T}}_k^i{\boldsymbol{h}}_{n + 1/2}^i + \left( {{\boldsymbol{M}}^i - \frac{{\Delta t}}{2}{\boldsymbol{T}}_d^i} \right){\boldsymbol{p}}_n^h (25) \begin{split} & \left(\mu {\boldsymbol{T}}_a^i + \frac{{\Delta t}}{2}\mu {\boldsymbol{T}}_b^i\right){\boldsymbol{h}}_{n + 3/2}^i = \left( {\mu {\boldsymbol{T}}_a^i - \frac{{\Delta t}}{2}\mu {\boldsymbol{T}}_b^i} \right){\boldsymbol{h}}_{n + 1/2}^i + \\&\qquad\quad \Delta t[ - \mu {\boldsymbol{T}}_c^i{\boldsymbol{p}}_{n + 1}^h - ({{\boldsymbol{S}}^i} - {\boldsymbol{F}}_{he}^{ii}){\boldsymbol{e}}_{n + 1}^i - \\&\qquad\quad {\boldsymbol{F}}_{he}^{ii}{\boldsymbol{e}}_{n + 1}^j + {\boldsymbol{F}}_{hh}^{ii}{\boldsymbol{h}}_{n + 1/2}^i - {\boldsymbol{F}}_{hh}^{ij}{\boldsymbol{h}}_{n + 1/2}^j] \end{split} (26) \left({\boldsymbol{M}}^i + \frac{{\Delta t}}{2}{\boldsymbol{T}}_d^i\right){\boldsymbol{p}}_{n + 3/2}^e = \Delta t{\boldsymbol{T}}_k^i{\boldsymbol{e}}_{n + 1}^i + \left( {{\boldsymbol{M}}^i - \frac{{\Delta t}}{2}{\boldsymbol{T}}_d^i} \right){\boldsymbol{p}}_{n + 1/2}^e (27) 1.3 局部时间步进
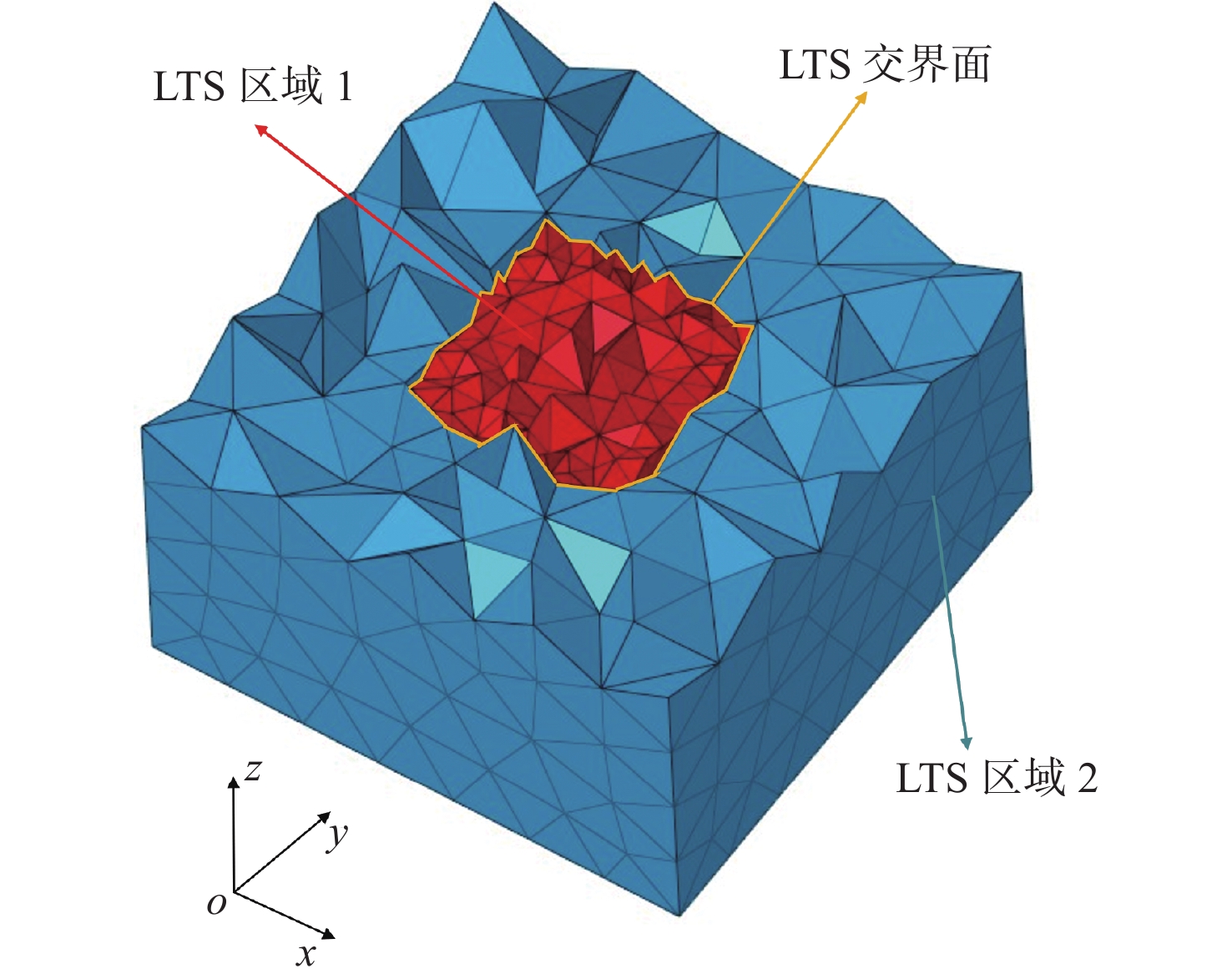
DGTD算法的时间步长受最小网格尺寸的限制，因此对于多尺度问题，其计算效率不高。在电磁屏蔽问题中，金属屏蔽体经常存在孔、槽等细小结构，为提高计算效率，本节将LTS法[32-34]引入到了DGTD算法中，以便更好地处理多尺度问题。LTS方法的实现分为以下4个步骤。
1） 如图3所示，根据模型中不同结构的实际物理尺寸，将整个计算域划分为不同的LTS区域。实际物理尺寸最小的区域用比较细的尺寸进行网格离散，标记为LTS区域1，其他区域可以用较粗的尺寸进行网格离散，标记为LTS区域2、LTS区域3等。
2） 根据CFL（Courent-Friedrichs-Lewy）条件[35]和LTS区域中的最小网格尺寸，计算每个LTS区域的局部时间步长 \Delta {t_i} ：
{c}_{i}\Delta {t}_{i}\left[\frac{4\sqrt{5}}{3}+\frac{8}{3}\mathrm{max}\left(\sqrt{\frac{{\mu }_{i}}{{\mu }_{j}}},\;\sqrt{\frac{{\varepsilon }_{i}}{{\varepsilon }_{j}}}\right)\right] \lt \frac{4{V}_{i}}{{P}_{i}} (28) 式中：ci为光速， {c_i} = 1/\sqrt {{\varepsilon _i}{\mu _i}} ； {V_i} 为LTS区域中最小单元的体积； {{P}_i} 为该最小单元4个面的总面积；下标j表示最小单元的相邻单元。
3） 设DGTD算法的全局时间步长 \Delta t 为最小 \Delta {t_i} ，即 \Delta {t_1} ，然后将局部时间步长 \Delta {t}_{i}(i=1,2,3,...) 重新设置为∆t的倍数：
\Delta {t_i} = {m_i}\Delta t (29) 式中， {m_i} 为一个严格的正整数。
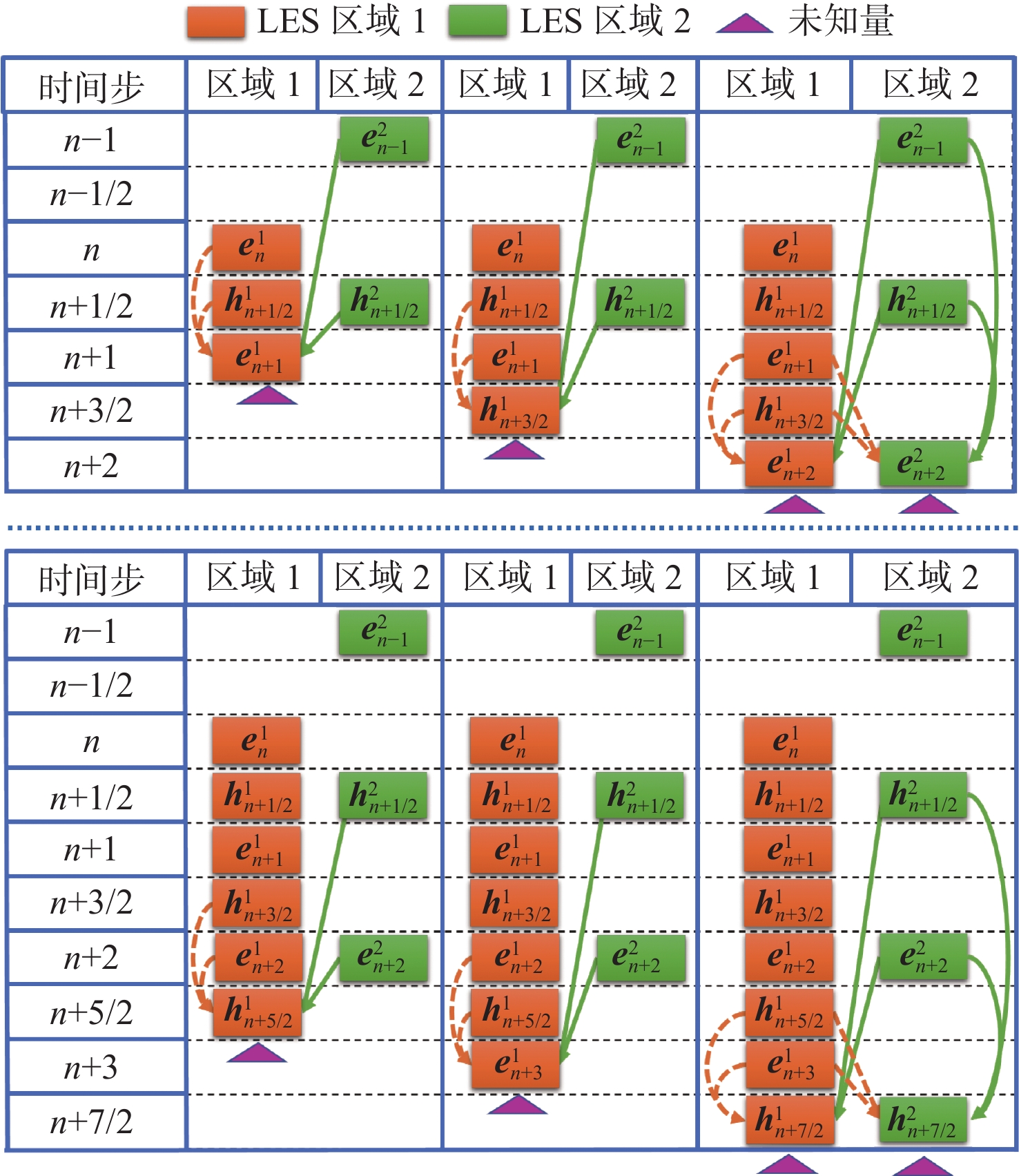
4）在每个LTS区域内进行局部时间步进。如图3所示，设LTS区域1的网格尺寸较小，而LTS区域2的网格尺寸则较大，根据前3步，将 {m_i} 设置为3，即 \Delta {t_1} = \Delta t ， \Delta {t_2} = 3\Delta t 。图4展示了LTS方法的具体求解过程（图中，Nt为总时间步数）。由式（9）和式（10）可知，如果要求解某一单元当前的电场和磁场，则需要求解该单元及其相邻单元前一时刻的电场和磁场。下面，将分4种情况讨论DGTD方程的解。
![]()
图 4 交界面上两组单元的局部时间步进求解过程Figure 4. Solving process of local time-stepping at the interface of two groups（1） 如果一个单元及其相邻单元都位于LTS区域1内，则该单元的DGTD矩阵方程用时间步长∆t求解，这可以从图4中区域1的列中观察到。电场和磁场均以∆t进行更新。
（2） 如果一个单元及其相邻单元都位于LTS区域2内，则该单元的DGTD矩阵方程用时间步长3∆t求解，这可以从图4中区域2的列中观察到。电场和磁场均以3∆t进行更新。
（3） 如果一个单元位于LTS区域1内，而其相邻单元位于LTS区域2内，即这2个单元位于区域1和区域2的交界面上，则与情形1）相比，该单元的DGTD矩阵方程仍用时间步长∆t求解。由于区域1和区域2的时间步长不同，在一些时刻，区域2中的电场和磁场是未知的，在这种情况下，直接调用区域2中最近一次更新的电场和磁场。例如，在图4中调用区域2中的 {\boldsymbol{e}}_{n - 1}^2 和 {\boldsymbol{h}}_{n + 1/2}^2 可以得到 {\boldsymbol{e}}_{n + 1}^1 ， {\boldsymbol{h}}_{n + 3/2}^1 和 {\boldsymbol{e}}_{n + 2}^1 的解。
（4） 类似地，如果一个单元位于LTS区域2内，而其相邻单元位于LTS区域1内，则与情形2）相比，该单元的DGTD矩阵方程仍用时间步长3∆t求解。在这种情况下，直接调用区域1中现有的最新电场和磁场。例如，在图4中调用在区域1中的 {\boldsymbol{e}}_{n + 1}^1 和 {\boldsymbol{h}}_{n + 3/2}^1 可以得到 {\boldsymbol{e}}_{n + 2}^2 的解。
由以上过程可以看出，采用局部时间步进法在LTS区域2中可以节省大量的计算，如图4所示，由 {\boldsymbol{h}}_{n + 1/2}^1 和 {\boldsymbol{h}}_{n + 1/2}^2 更新到 {\boldsymbol{h}}_{n + 7/2}^1 和 {\boldsymbol{h}}_{n + 7/2}^2 ，区域1中的单元需要求解6次方程，而区域2中的单元则只需求解2次方程。
1.4 LTS-DGTD并行技术
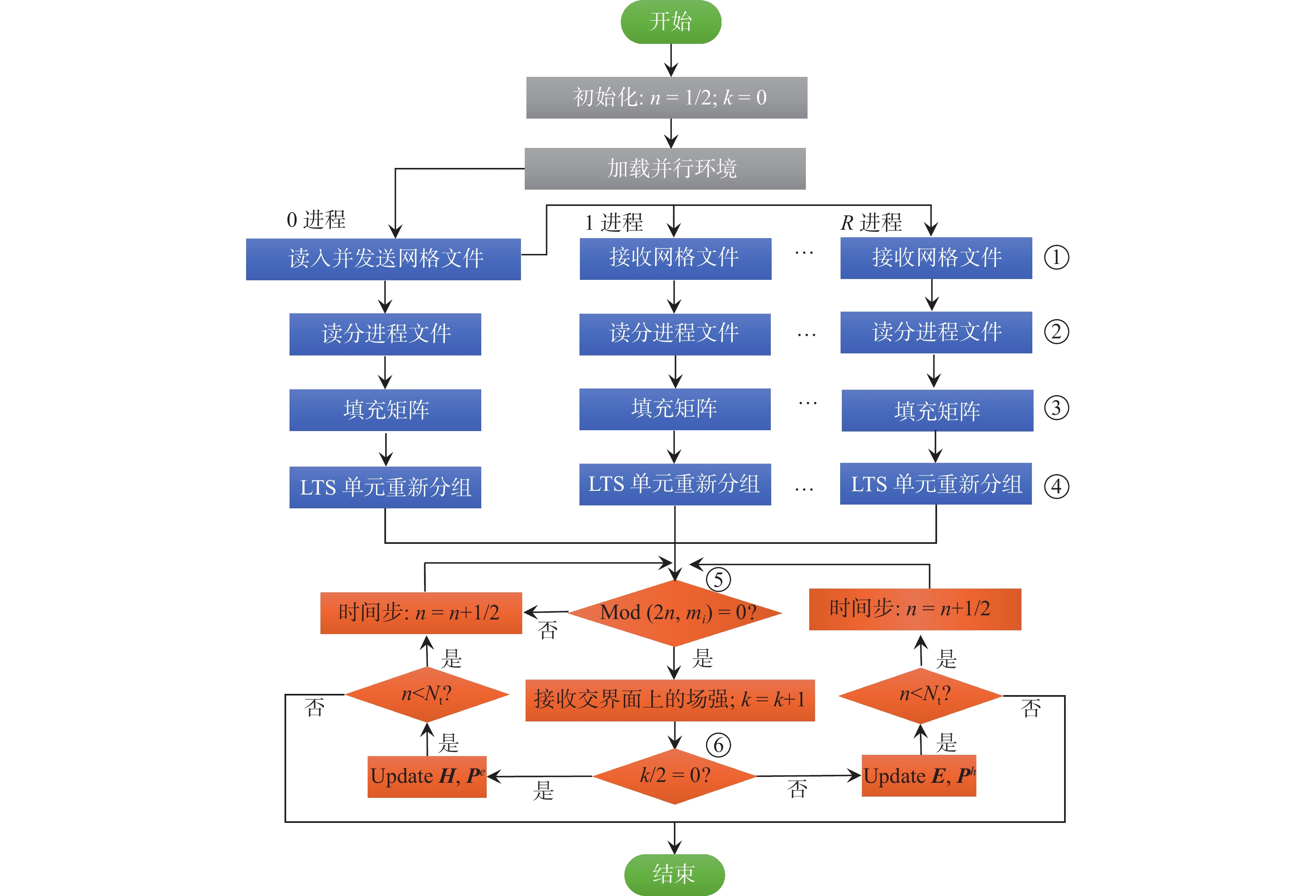
为进一步提高计算速度，采用消息传递接口（MPI）技术对LTS-DGTD方法进行并行化设计。通过METIS软件[36]对原始网格进行均匀分组，以使相邻两进程交界面上的单元数量最小，R为总进程数。接下来，将根据图5所示的并行策略，介绍LTS-DGTD方法的并行计算过程。
1） 0进程作为主进程，读取网格文件，并将网格信息发送给其他进程。
2） 每个进程都读取METIS的分进程文件，并决定需要处理哪些四面体单元。
3） 每个进程都填充非PML区域矩阵和PML区域矩阵。
4） 每个进程根据对需要处理的单元进行LTS区域分组并重新编号，以建立全局单元号与LTS区域局部单元号之间的映射关系。
5） 每个进程通过判断 \text{Mod}(\text{2}n，{m}_{i})=0 是否成立决定一组LTS单元是否跳过时间步进。
6） 用一个标志数k来控制电场和磁场交替地进行时间步进。根据式（24）～式（27），通常 {{{\boldsymbol{P}}}^h} 和电场一起求解，而 {{{\boldsymbol{P}}}^e} 则和磁场一起求解。
2. 数值算例
首先，采用本文所提方法对带矩形孔的金属屏蔽体进行数值仿真，并将仿真结果与采用商业软件所得结果进行对比，验证所提方法的正确性。然后，在此基础上探讨各种设计参数对金属屏蔽体时域屏蔽效能的影响。除非另有说明，本节的算例仿真均是在20核的Intel Xeon Gold 6230 CPU、内存为128 GB 的工作站上执行，如未特别说明，并行计算结果均是基于16个CPU核并行。
2.1 LTS-DGTD的正确性验证
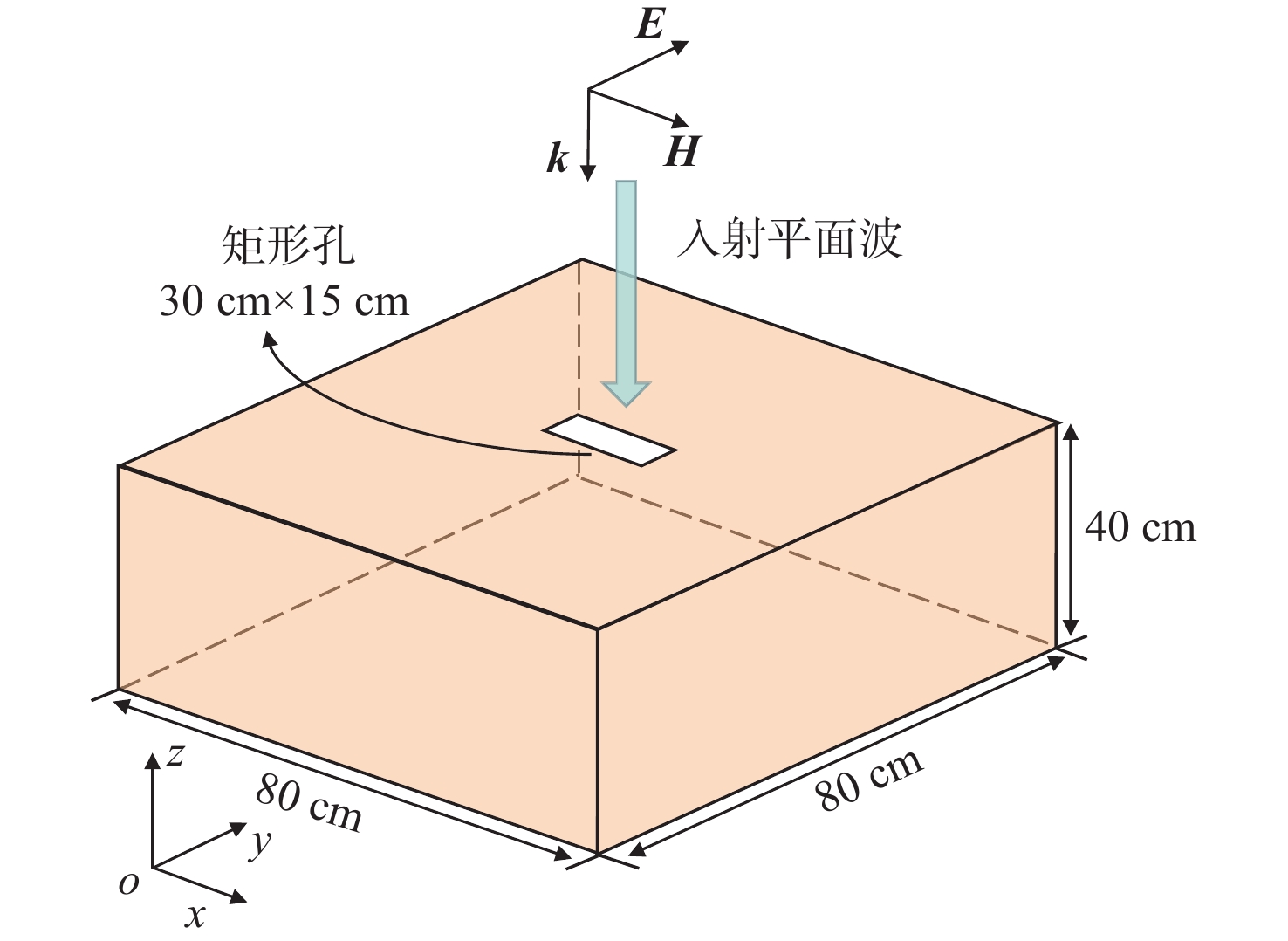
如图6所示，金属屏蔽体的上表面中心有一个30 cm × 15 cm的矩形孔。屏蔽体长80 cm，宽80 cm，高40 cm。平面波入射方向沿负z轴，如图中k所示，入射波电场极化方向沿正y轴，如图中E所示，激励源是幅值为1 V/m的调制高斯脉冲，其中心频率为300 MHz。假定腔体无厚度，在其表面施加理想的电导体（perfect electric conductort，PEC）边界条件。如图7所示，整个计算域被划分为3个LTS区域。LTS区域1包含整个矩形孔，LTS区域2包含整个金属腔，其余为LTS区域3。每个LTS区域的单元数量、 \Delta {t_i} 和 {m_i} 如表1所示。总仿真时间设置为90 ns，总时间步数为200 000。
![]()
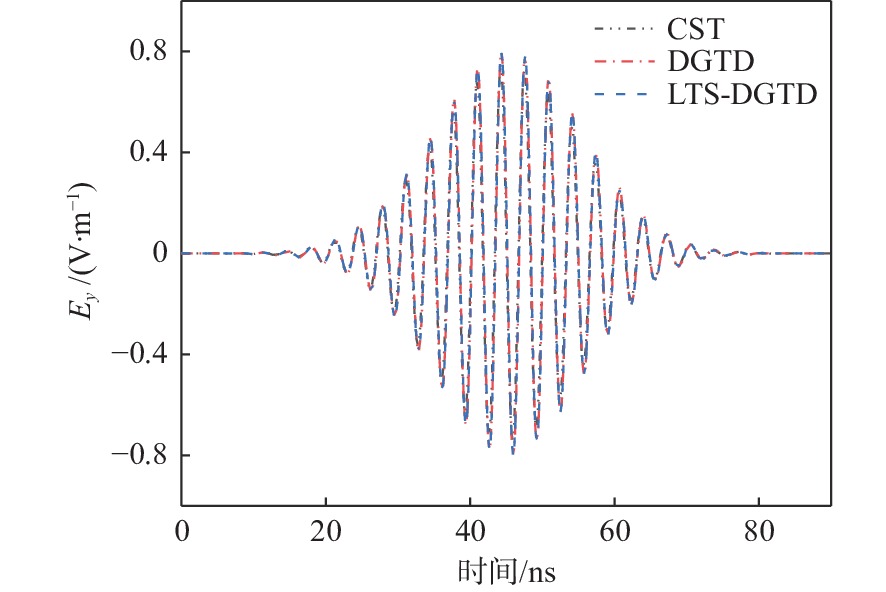
图 6 带矩形孔的金属屏蔽腔模型图Figure 6. The model of metallic enclosure with a rectangular aperture如图8所示，采用商业软件CST、传统DGTD算法和本文所提LTS-DGTD方法得到的腔体中心（0 mm，0 mm，0 mm）处的瞬态电场 {E_y} 吻合较好。同时，对比了串行DGTD、并行DGTD和并行LTS-DGTD方法的仿真速度，此时，总仿真时间设置为4.5 ns。由表2可以看到，采用本文所提LTS-DGTD方法可以有效地加速仿真。可见，采用本文所提方法可以加速后续对影响金属屏蔽体时域屏蔽效能的各种设计参数的研究。此外，本节中其他案例的腔体大小、入射波设置以及采样点均与本算例一致。
表 1 3个LTS区域的单元数量和时间步长Table 1. The number of mesh elements and time step for three LTS zones单元数量 \Delta {t_i} /s {m_i} LTS区域1 28 783 4.5×10−13 1 LTS区域2 42 921 1.8×10−12 4 LTS区域3 55 929 7.2×10−12 16 表 2 不同方法下的CPU时间比较Table 2. CPU time comparison of different methods方法 耗时/min 串行DGTD 419.5 并行DGTD 42.7 并行LTS-DGTD 17.1 ![]()
图 8 腔体中心处沿极化方向的电场强度Figure 8. Electric field intensity in polarization direction at the center of the enclosure为了评估并行LTS-DGTD方法的并行性能，表3给出了计算时间、并行效率与并行计算中使用的CPU核数之间的关系。从中可以发现，并行LTS-DGTD方法的并行效率较高。
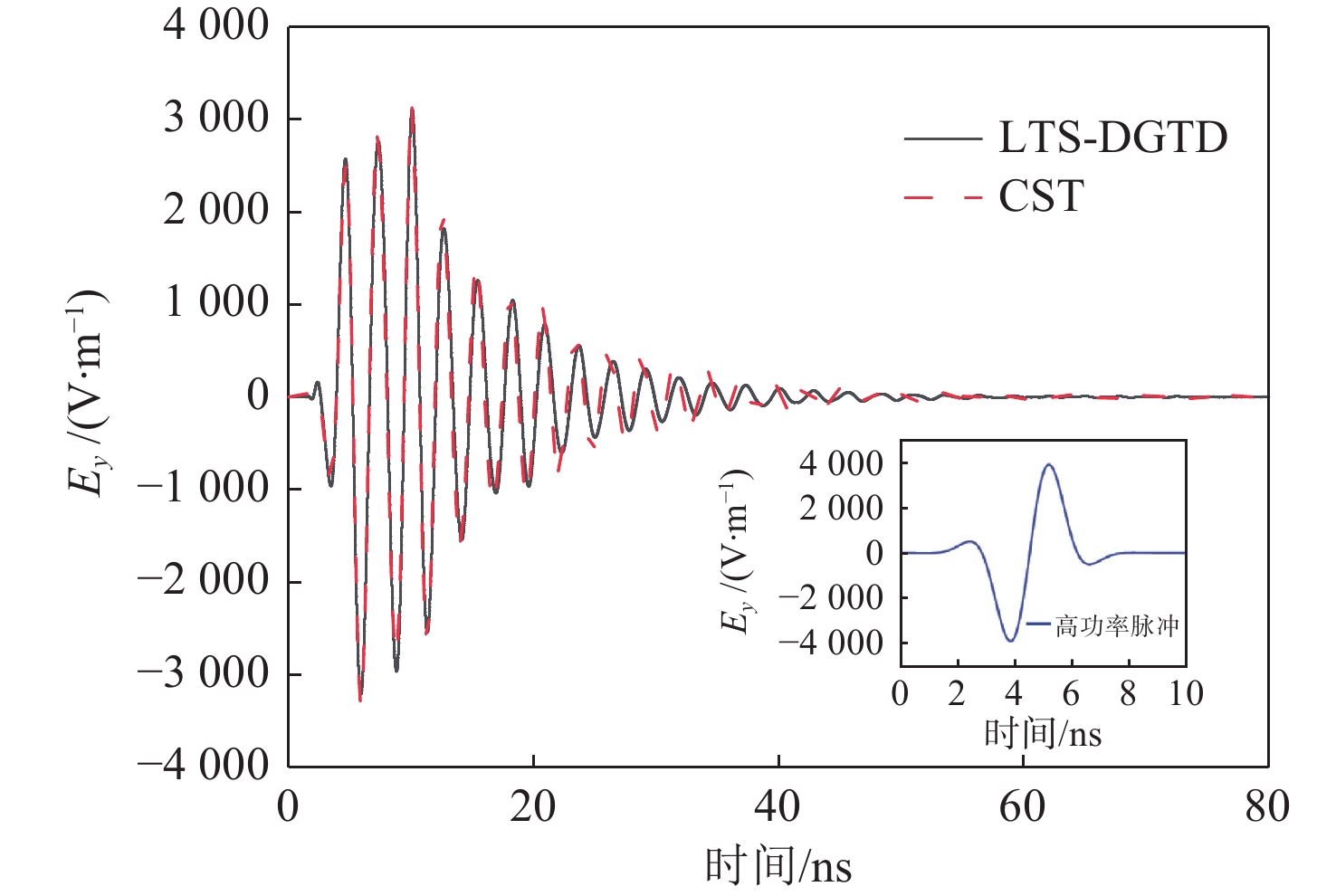
表 3 LTS-DGTD方法的CPU时间与并行效率Table 3. CPU time and parallel efficiency of LTS-DGTD核数 CPU时间/h 并行效率/% 4 22.8 100 8 12.5 91.2 16 6.4 89.1 32 3.4 83.8 48 2.6 73.1 为了检验算法平台的鲁棒性，用高功率电磁脉冲照射如图6所示的金属屏蔽腔，激励源为幅值为5 000 V/m的调制高斯脉冲，其波形如图9所示。最小时间步长为 \Delta t = 4 \times {10^{ - 13}}\;{\rm{s}} ，总时间步数是200000，总仿真时间设置为80 ns， LTS区域设置及 {m_i} 的取值与上一算例保持一致。仿真结果如图9所示。由图可见，采用 LTS-DGTD方法所得仿真结果与采用商业软件CST所得结果吻合较好。同时，还对比了传统并行DGTD方法和并行LTS-DGTD方法的仿真速度，此时，总仿真时间设置为4.5 ns。结果显示采用传统并行DGTD方法的耗时为59.9 min，采用并行LTS-DGTD方法的耗时为19.8 min，引入LTS后的计算速度为原来的3.03倍。由表2可知，在上一算例中传统并行DGTD方法和并行LTS-DGTD方法的耗时分别为42.7 和17.1 min，引入LTS后计算速度为原来的2.5倍。本算例相对上一算例其加速效果有所提升，其原因是本算例的时间步长与上一算例相比有所减小，故LTS的加速效果更加明显。
![]()
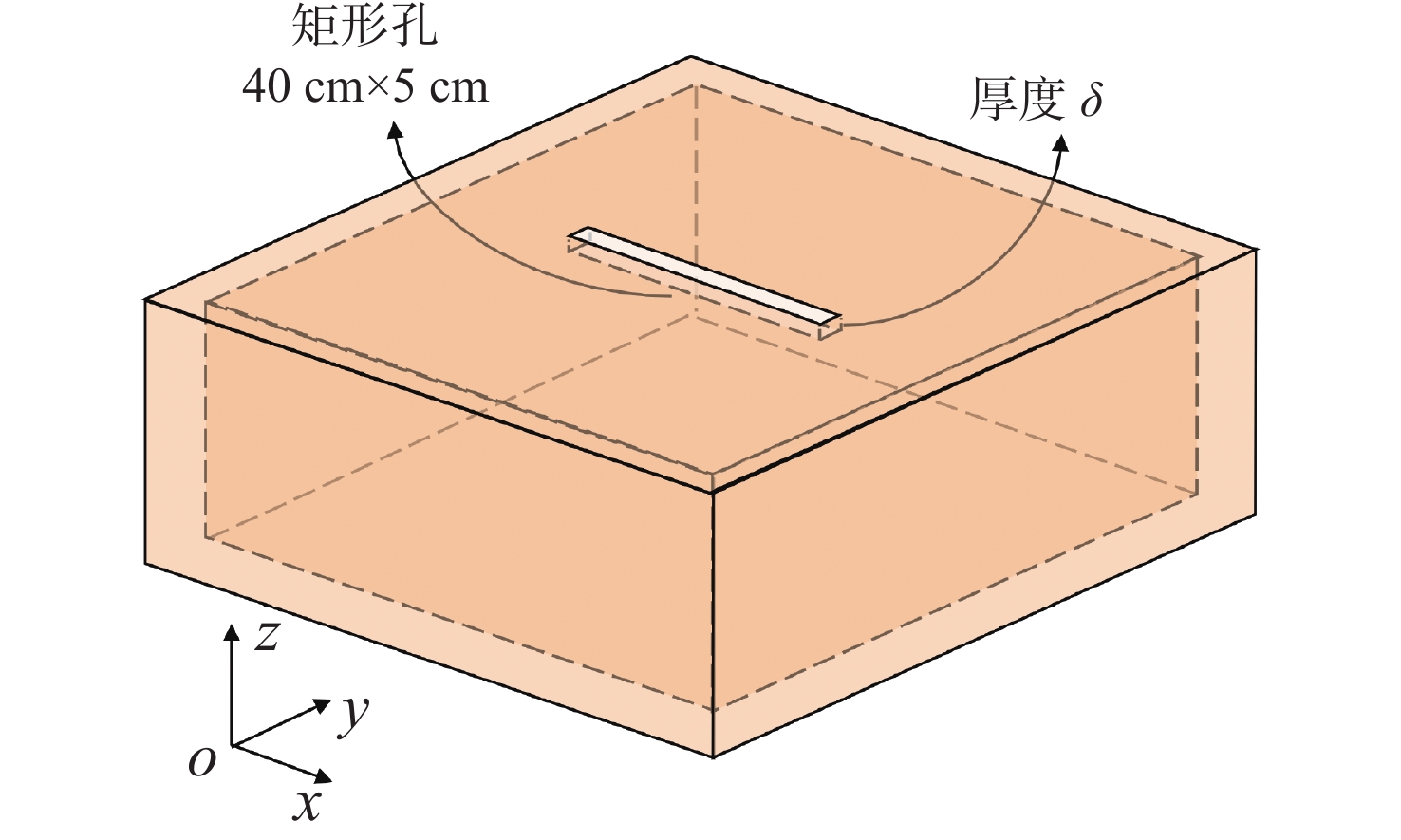
图 9 高功率脉冲照射下观察点处沿极化方向的电场强度Figure 9. Electric field intensity in polarization direction at the observation point under high power pulse irradiation2.2 腔体厚度对TDSE的影响
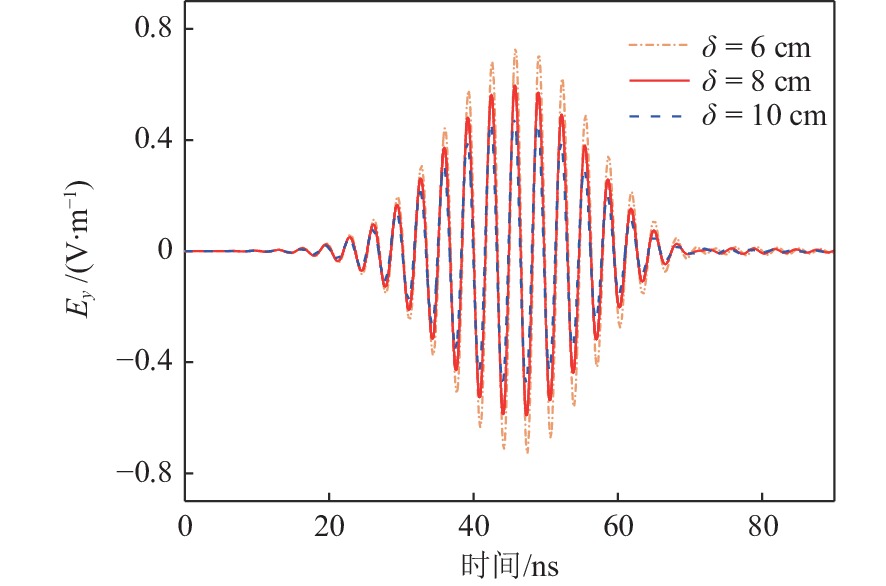
如图10所示，在第2个算例中，固定矩形孔的尺寸为40 cm × 5 cm，金属屏蔽腔体内壁尺寸不变，研究腔体厚度δ对TDSE的影响。图11给出了δ为6，8，10 cm时观察点处的瞬态电场。从图中可以看到，电场的振幅是随厚度的增加而减小的。常用的TDSE有3种[22]，分别为峰值衰减屏蔽效能、导数衰减屏蔽效能和能量密度衰减屏蔽效能。本文取峰值衰减屏蔽效能来表示TDSE。
![]()
图 10 带矩形孔的腔体厚度有限的金属屏蔽腔结构Figure 10. The construction of a metallic enclosure with a rectangular aperture of finite thickness![]()
图 11 腔体厚度对金属屏蔽腔中心电场Ey的影响Figure 11. Effect of thickness on Ey in the center of the metallic enclosure{TDSE} = 20 \lg \frac{{\mathop {\max }\limits_n \left| {{{\boldsymbol{E}}^{\rm{in}}}({{\boldsymbol{r}}_{\rm{o}}},n\Delta t)} \right|}}{{\mathop {\max }\limits_n \left| {{{\boldsymbol{E}}^s}({{\boldsymbol{r}}_{\rm{o}}},n\Delta t)} \right|}} (30) 式中： {{\boldsymbol{E}}^{\rm{in}}} ， {{\boldsymbol{E}}^s} 分别为无屏蔽时和有屏蔽时观察点处的电场强度；整个式子的分子为无屏蔽时观察点 {{\boldsymbol{r}}_{\rm{o}}} 处入射电场振幅的最大值；分母为有屏蔽时同一观察点处最大电场幅值。
由表4可知，TDSE是随金属屏蔽腔厚度的增加而增大的。究其原因，发现增加腔体厚度相当于增加了孔径附近的面积，从而会产生额外的表面电流。根据Araneo等[37]的理论，由于金属屏蔽腔内的辐射源减少了，因此TDSE便会增大。
表 4 金属屏蔽腔厚度对TDSE的影响Table 4. Effect of metallic enclosure thickness on TDSE腔体厚度δ/cm Ey最大幅值/(V∙m−1) TDSE/dB 6 0.72 2.85 8 0.58 4.73 10 0.45 6.93 2.3 矩形孔短边边长对TDSE的影响
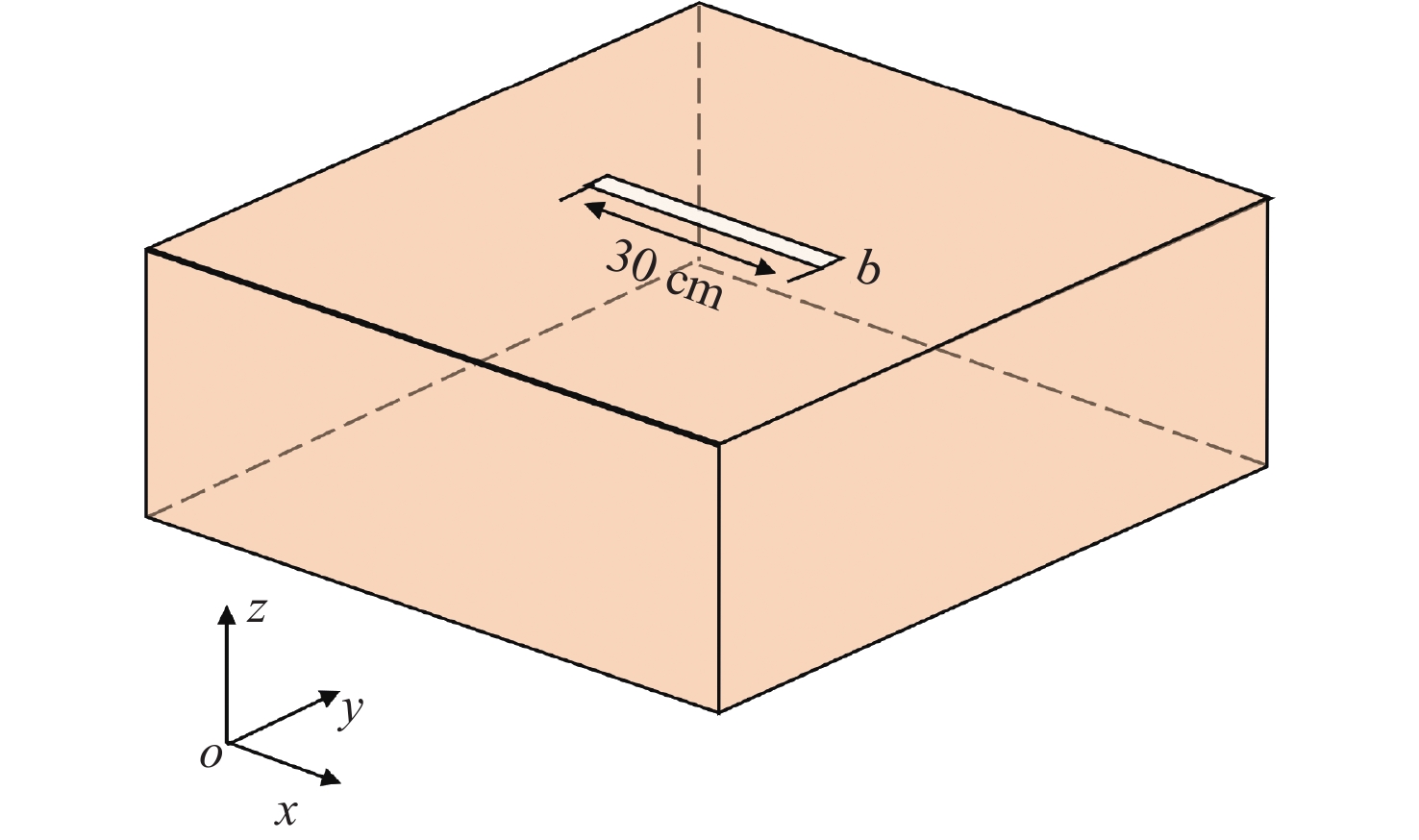
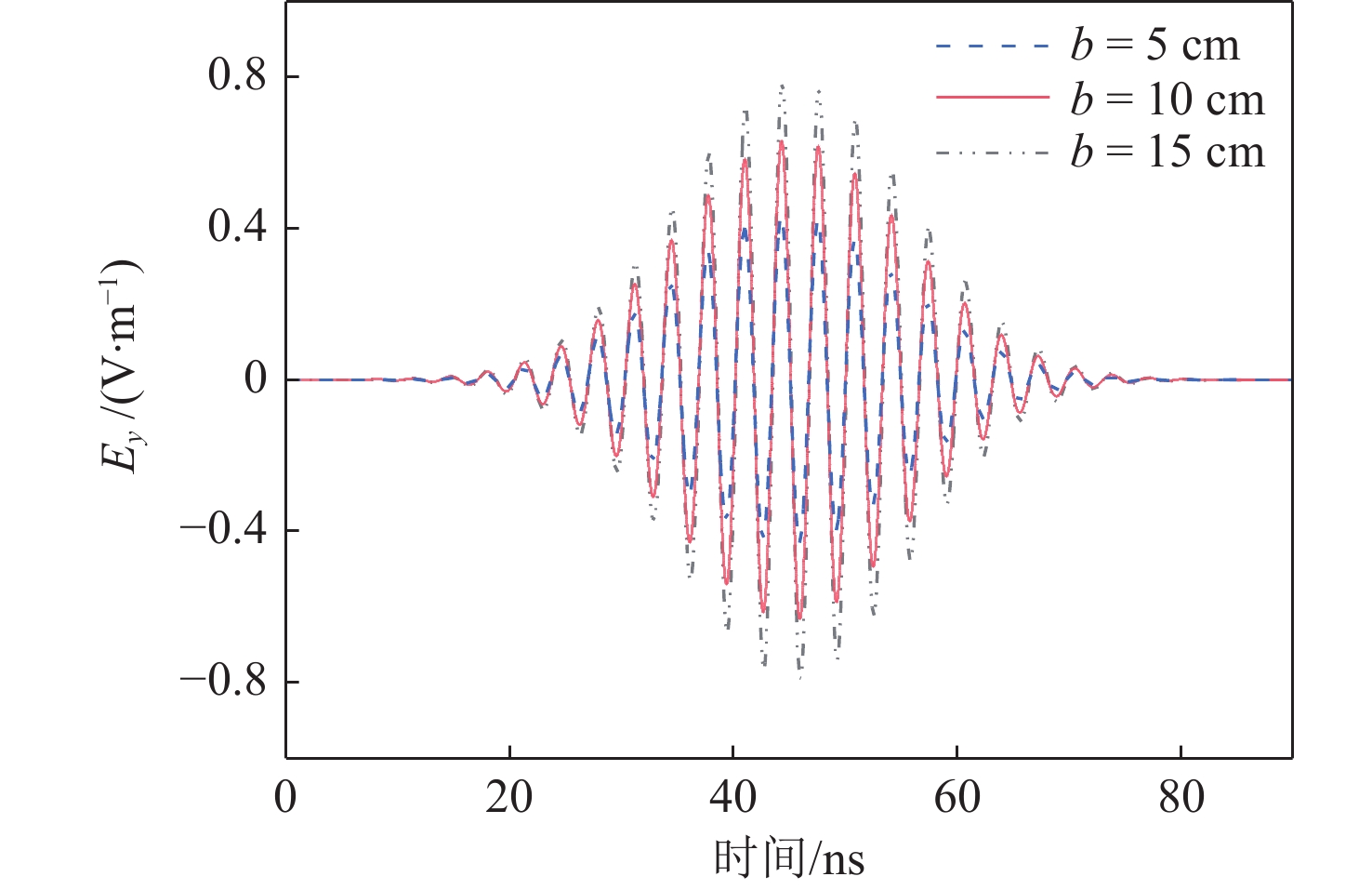
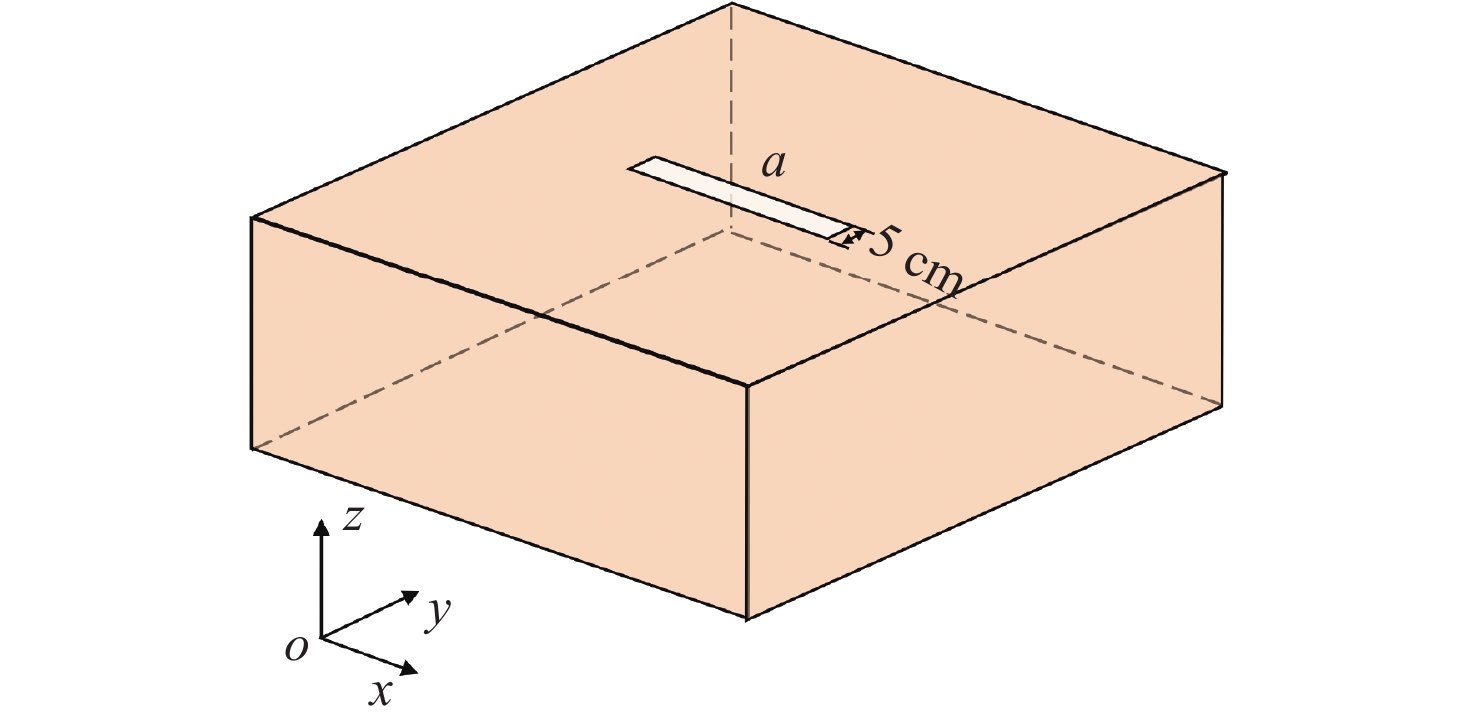
如图12所示，固定矩形孔长边长度a为30 cm，研究短边长度b对TDSE的影响。图13所示为b为5，10，15 cm时金属屏蔽腔中心的瞬态电场。从图中可以看到，观察点处的电场强度是随短边长度b的增加而增大的。根据表5，可以得出短边越短TDSE越大的结论。将矩形孔看成是一个天线，其短边长度的减小相当于天线有效接收面积的减小，这样会削弱天线接收电磁波的能力，由此进入屏蔽腔体的内部电场强度也会变小，计算得到的TDSE则会增大。
![]()
图 12 保持长边边长恒定为30 cm时的矩形孔示意图Figure 12. Schematic diagram of rectangular aperture keeping the long side length constant to 30 cm![]()
图 13 矩形孔短边边长对金属屏蔽腔中心电场Ey的影响Figure 13. Effect of short side length on the center electric field Ey of the metallic enclosure表 5 矩形孔短边边长对TDSE的影响Table 5. Effect of short side length of rectangular aperture on TDSE短边边长b/cm Ey最大幅值/(V∙m−1) TDSE/dB 5 0.42 7.53 10 0.63 4.01 15 0.79 2.04 2.4 矩形孔长边边长对TDSE的影响
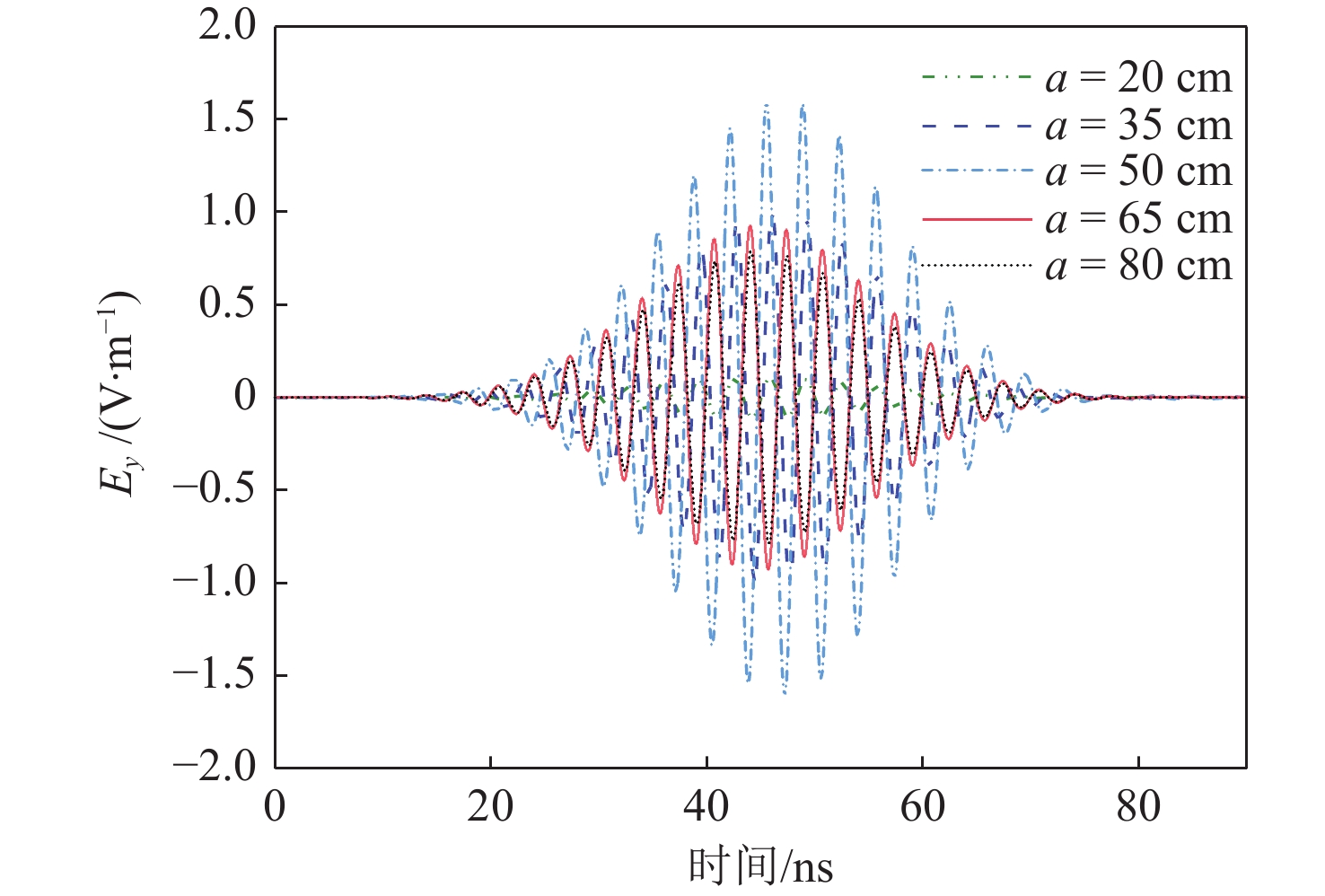
如图14所示，固定矩形孔短边长度b为5 cm，研究长边长度a对TDSE的影响。图15给出的是a为20 ，35，50，65，80 cm时金属屏蔽腔中心的瞬态电场。从图中可以看出，电场的振幅随长边长度的变化不是单调的。更具体地说，当a值接近于入射波的一半波长（本例中为50 cm）时，电场的振幅最大。表6给出了5种相应情况下计算得到的TDSE值。从表中可以看到，当a = 50 cm时，TDSE为−4.02 dB，负值表示设计的屏蔽效果相比没有金属外屏蔽体时更差。综上所述，当矩形孔的长边边长接近于入射波的一半波长时，TDSE会变差。这种现象也可以采用天线理论解释。将矩形孔看成是一个缝隙天线，当长边接近于入射波的一半波长时，天线工作在谐振模式附近，此时，天线耦合的能量比较大，导致TDSE较小。
![]()
图 14 保持短边长度恒定为5 cm的矩形孔示意图Figure 14. Schematic diagram of rectangular aperture keeping the short side length constant to 5 cm![]()
图 15 矩形孔长边边长对金属屏蔽腔中心电场Ey的影响Figure 15. Effect of long side length on the center electric field Ey of the metallic enclosure表 6 矩形孔长边边长对TDSE的影响Table 6. Effect of long side length of rectangular aperture on TDSE长边边长a/cm Ey最大幅值/(V∙m−1) TDSE/dB 20 0.10 20.00 35 1.00 0 50 1.59 -4.02 65 0.92 0.72 80 0.78 2.15 2.5 孔径阵列间距对TDSE的影响
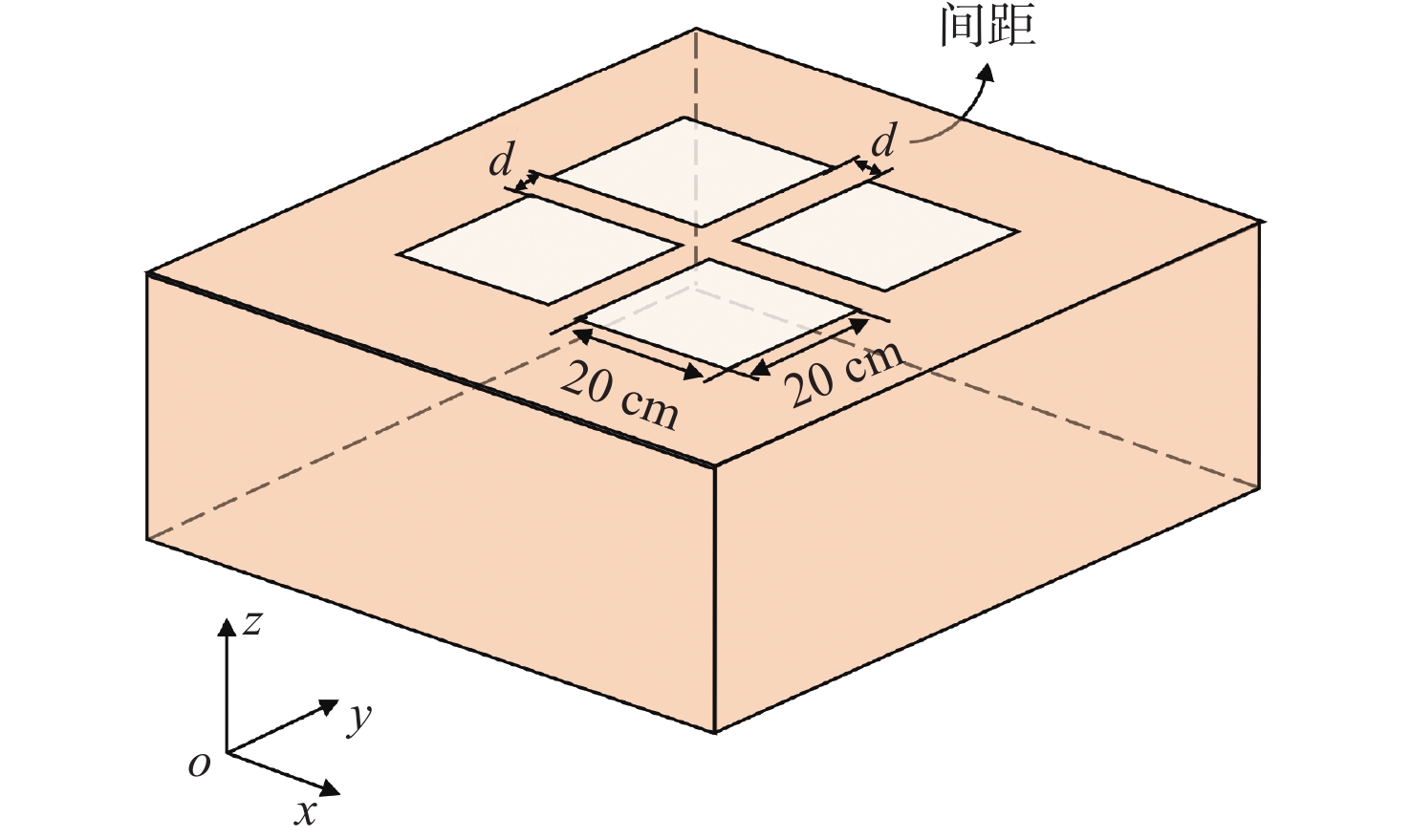
如图16所示，研究了2×2阵列孔间距的影响。孔径尺寸为20 cm× 20 cm，阵列单元间的间距d在x，y方向是相同的。图17所示为d = 2，6，10 cm时金属屏蔽腔中心的瞬态电场。由表7可见，TDSE是随间距d的增大而增大。间距的增大减小了孔与孔之间的耦合[38]，因此，进入金属屏蔽腔体内部的的电场会减少，TDSE增大。
![]()
图 16 不同间距的孔阵列结构图Figure 16. Structure diagram of aperture array with variable spacings![]()
图 17 孔阵列间距对金属屏蔽腔中心电场Ey的影响Figure 17. Effect of spacing of aperture array elements on the center electric field Ey of the metallic enclosure表 7 孔阵列间距对TDSE的影响Table 7. Effect of spacing of aperture array elements on TDSE孔阵列间距d/cm Ey最大幅值/(V∙m−1) TDSE/dB 2 0.88 1.11 6 0.53 5.51 10 0.39 8.17 2.6 孔阵列单元数对TDSE的影响
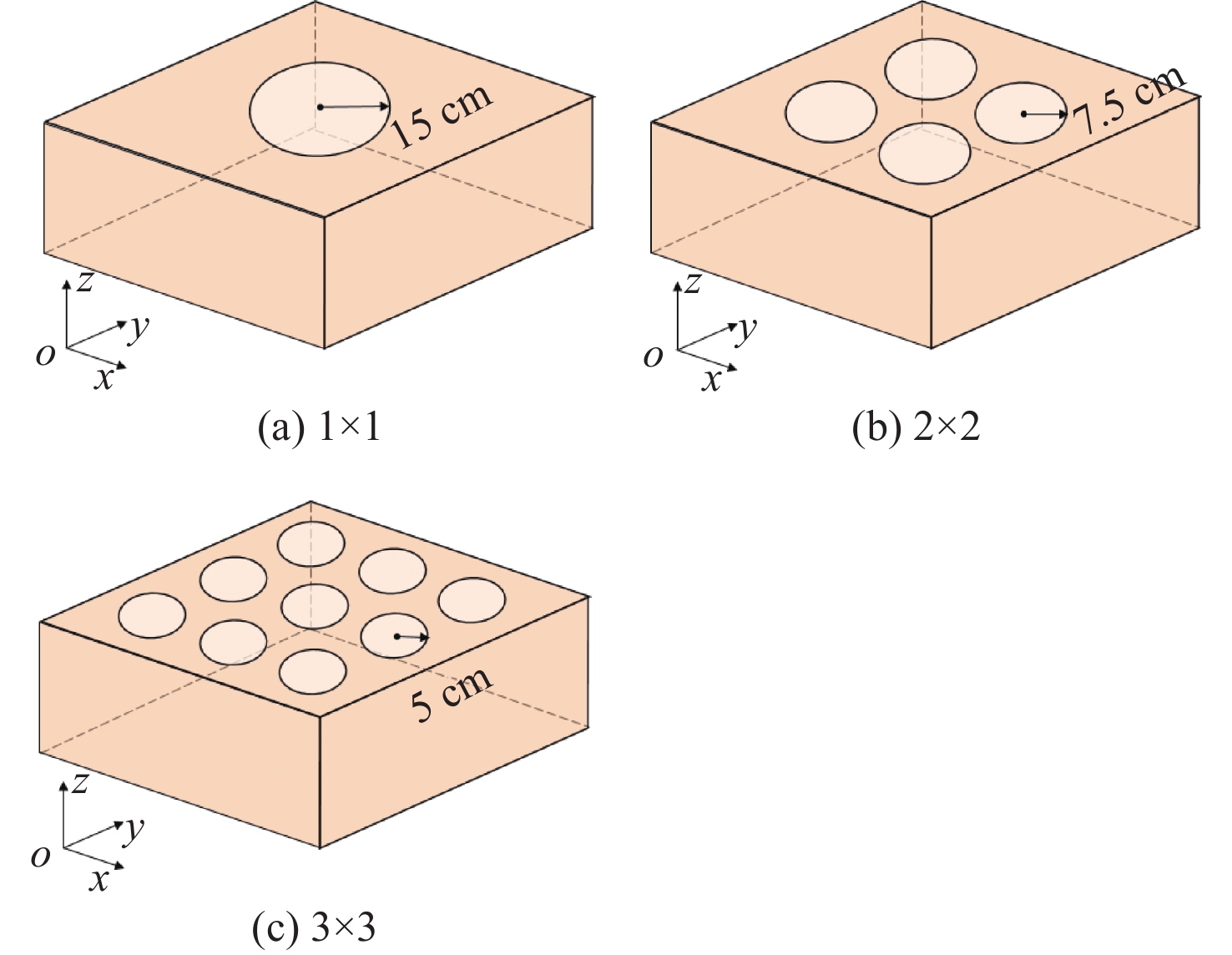
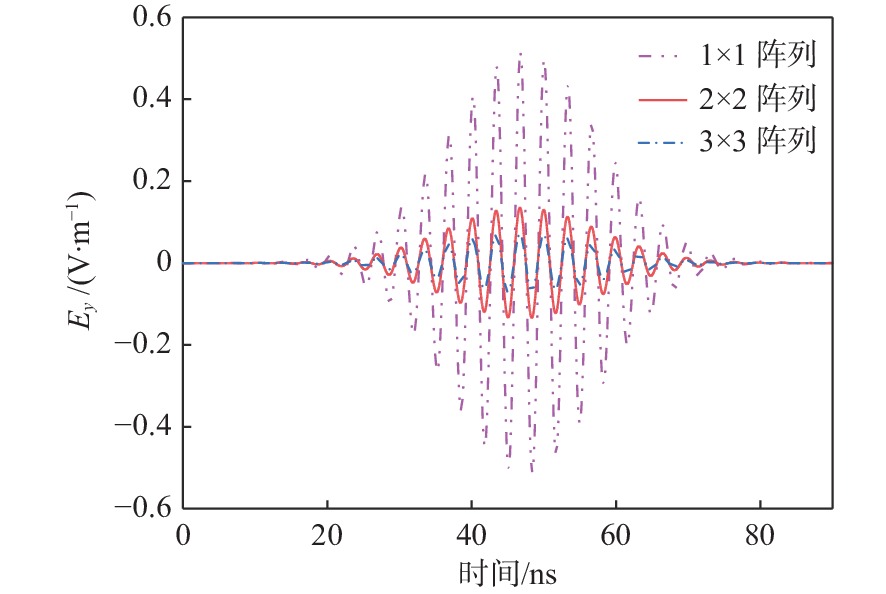
如图18所示，固定孔的总面积为225π cm2，孔间距固定为5 cm，研究孔阵列单元数对TDSE的影响。图19显示了孔阵列单元数分别为1 × 1，2 × 2和3 × 3时金属屏蔽腔中心的瞬态电场。从图中可以看到，随着孔阵列单元数量的增加，进入金属屏蔽体的电场变小。TDSE的值汇总于表8中，由表可见，随着孔阵列单元数量的增越多，TDSE越高。这是因为孔径阵列的总面积是固定的，孔阵列单元数的增加会使每个孔的面积减小，从而增大TDSE。
![]()
图 19 孔阵列单元数对金属屏蔽腔中心电场Ey的影响Figure 19. Effect of the number of aperture array elements on the center electric field Ey of the metallic enclosure表 8 孔阵列单元数对TDSE的影响Table 8. Effect of the number of aperture array elements on TDSE孔阵列单元数 Ey最大幅值/(V∙m−1) TDSE/dB 1×1 0.51 5.85 2×2 0.14 17.07 3×3 0.07 23.09 3. 结 论
本文采用DGTD算法对金属屏蔽腔的TDSE进行了分析，并采用LTS和并行技术加速了仿真过程，结果显示本文所提方法可为电磁屏蔽问题的仿真提供一种有效工具。随后，通过该方法在时域上对频域中一系列广为认可的屏蔽效果规律进行了验证。最后，从TDSE的角度给出了带孔金属屏蔽腔的设计规则：
1） 适当增加金属屏蔽腔腔体的厚度可以获得更好的屏蔽效果；
2） 设计矩形孔时，边长越短，TDSE越大，但应避免边长长度接近于入射波的半波长；
3） 对于一定数量的阵列孔，合理增大孔阵列间距可以获得更好的屏蔽效果；
4） 在孔的总面积一定的情况下，增加孔阵列单元数可以有效增大TDSE。
-
![]()
图 1 金属屏蔽体屏蔽效能分析的三维计算域
Figure 1. The 3-D computational domain for the shielding effectiveness analysis of metallic enclosure
![]()
图 2 金属屏蔽体屏蔽效能分析的二维计算域
Figure 2. The 2-D computational domain for the shielding effectiveness analysis of metallic enclosure
![]()
图 4 交界面上两组单元的局部时间步进求解过程
Figure 4. Solving process of local time-stepping at the interface of two groups
![]()
图 6 带矩形孔的金属屏蔽腔模型图
Figure 6. The model of metallic enclosure with a rectangular aperture
![]()
图 8 腔体中心处沿极化方向的电场强度
Figure 8. Electric field intensity in polarization direction at the center of the enclosure
![]()
图 9 高功率脉冲照射下观察点处沿极化方向的电场强度
Figure 9. Electric field intensity in polarization direction at the observation point under high power pulse irradiation
![]()
图 10 带矩形孔的腔体厚度有限的金属屏蔽腔结构
Figure 10. The construction of a metallic enclosure with a rectangular aperture of finite thickness
![]()
图 11 腔体厚度对金属屏蔽腔中心电场Ey的影响
Figure 11. Effect of thickness on Ey in the center of the metallic enclosure
![]()
图 12 保持长边边长恒定为30 cm时的矩形孔示意图
Figure 12. Schematic diagram of rectangular aperture keeping the long side length constant to 30 cm
![]()
图 13 矩形孔短边边长对金属屏蔽腔中心电场Ey的影响
Figure 13. Effect of short side length on the center electric field Ey of the metallic enclosure
![]()
图 14 保持短边长度恒定为5 cm的矩形孔示意图
Figure 14. Schematic diagram of rectangular aperture keeping the short side length constant to 5 cm
![]()
图 15 矩形孔长边边长对金属屏蔽腔中心电场Ey的影响
Figure 15. Effect of long side length on the center electric field Ey of the metallic enclosure
![]()
图 16 不同间距的孔阵列结构图
Figure 16. Structure diagram of aperture array with variable spacings
![]()
图 17 孔阵列间距对金属屏蔽腔中心电场Ey的影响
Figure 17. Effect of spacing of aperture array elements on the center electric field Ey of the metallic enclosure
![]()
图 19 孔阵列单元数对金属屏蔽腔中心电场Ey的影响
Figure 19. Effect of the number of aperture array elements on the center electric field Ey of the metallic enclosure
表 1 3个LTS区域的单元数量和时间步长
Table 1 The number of mesh elements and time step for three LTS zones
单元数量 \Delta {t_i} /s {m_i} LTS区域1 28 783 4.5×10−13 1 LTS区域2 42 921 1.8×10−12 4 LTS区域3 55 929 7.2×10−12 16 
下载: 导出CSV
表 2 不同方法下的CPU时间比较
Table 2 CPU time comparison of different methods
方法 耗时/min 串行DGTD 419.5 并行DGTD 42.7 并行LTS-DGTD 17.1
下载: 导出CSV
表 3 LTS-DGTD方法的CPU时间与并行效率
Table 3 CPU time and parallel efficiency of LTS-DGTD
核数 CPU时间/h 并行效率/% 4 22.8 100 8 12.5 91.2 16 6.4 89.1 32 3.4 83.8 48 2.6 73.1
下载: 导出CSV
表 4 金属屏蔽腔厚度对TDSE的影响
Table 4 Effect of metallic enclosure thickness on TDSE
腔体厚度δ/cm Ey最大幅值/(V∙m−1) TDSE/dB 6 0.72 2.85 8 0.58 4.73 10 0.45 6.93
下载: 导出CSV
表 5 矩形孔短边边长对TDSE的影响
Table 5 Effect of short side length of rectangular aperture on TDSE
短边边长b/cm Ey最大幅值/(V∙m−1) TDSE/dB 5 0.42 7.53 10 0.63 4.01 15 0.79 2.04
下载: 导出CSV
表 6 矩形孔长边边长对TDSE的影响
Table 6 Effect of long side length of rectangular aperture on TDSE
长边边长a/cm Ey最大幅值/(V∙m−1) TDSE/dB 20 0.10 20.00 35 1.00 0 50 1.59 -4.02 65 0.92 0.72 80 0.78 2.15
下载: 导出CSV
表 7 孔阵列间距对TDSE的影响
Table 7 Effect of spacing of aperture array elements on TDSE
孔阵列间距d/cm Ey最大幅值/(V∙m−1) TDSE/dB 2 0.88 1.11 6 0.53 5.51 10 0.39 8.17
下载: 导出CSV
表 8 孔阵列单元数对TDSE的影响
Table 8 Effect of the number of aperture array elements on TDSE
孔阵列单元数 Ey最大幅值/(V∙m−1) TDSE/dB 1×1 0.51 5.85 2×2 0.14 17.07 3×3 0.07 23.09
下载: 导出CSV
-
[1] RADASKY W A, HOAD R. Recent developments in high power EM (HPEM) standards with emphasis on high altitude electromagnetic pulse (HEMP) and intentional electromagnetic interference (IEMI)[J]. IEEE Letters on Electromagnetic Compatibility Practice and Applications, 2020, 2(3): 62–66. doi: 10.1109/LEMCPA.2020.3009236
[2] SHOURVARZI A, JOODAKI M. Shielding effectiveness estimation of a metallic enclosure with an aperture using S-parameter analysis: analytic validation and experiment[J]. IEEE Transactions on Electromagnetic Com-patibility, 2017, 59(2): 537–540. doi: 10.1109/TEMC.2016.2615525
[3] BETHE H A. Theory of diffraction by small holes[J]. Physical Review, 1944, 66(7/8): 163–182.
[4] ROBINSON M P, BENSON T M, CHRISTOPOULOS C, et al. Analytical formulation for the shielding effectiveness of enclosures with apertures[J]. IEEE Transactions on Electromagnetic Compatibility, 1998, 40(3): 240–248. doi: 10.1109/15.709422
[5] NIE B L, LIU Q S, DU P A. An improved thickness correction method of analytical formulations for shielding effectiveness prediction[J]. IEEE Transactions on Electromagnetic Compatibility, 2016, 58(3): 907–910. doi: 10.1109/TEMC.2016.2533661
[6] LIU E B, DU P A, NIE B L. An extended analytical formulation for fast prediction of shielding effectiveness of an enclosure at different observation points with an off-axis aperture[J]. IEEE Transactions on Electromagnetic Compatibility, 2014, 56(3): 589–598. doi: 10.1109/TEMC.2013.2289742
[7] NIE B L, DU P A, XIAO P. An improved circuital method for the prediction of shielding effectiveness of an enclosure with apertures excited by a plane wave[J]. IEEE Transactions on Electromagnetic Compatibility, 2018, 60(5): 1376–1383. doi: 10.1109/TEMC.2017.2761399
[8] SARTO M S. A new model for the FDTD analysis of the shielding performances of thin composite structures[J]. IEEE Transactions on Electromagnetic Compatibility, 1999, 41(4): 298–306. doi: 10.1109/15.809798
[9] YAN L P, FANG M J, ZHAO X, et al. Efficient shielding effectiveness prediction of metallic structures with three-dimensional arbitrary thin slots using extended CP-FDTD[J]. IEEE Transactions on Electromagnetic Compatibility, 2019, 61(4): 1353–1361. doi: 10.1109/TEMC.2019.2909989
[10] CHEN J, WANG J G. A three-dimensional semi-implicit FDTD scheme for calculation of shielding effectiveness of enclosure with thin slots[J]. IEEE Transactions on Electromagnetic Compatibility, 2007, 49(2): 354–360. doi: 10.1109/TEMC.2007.893329
[11] CHEN J, GUO J Y, TIAN C M. Analyzing the shielding effectiveness of a graphene-coated shielding sheet by using the HIE-FDTD method[J]. IEEE Transactions on Electromagnetic Compatibility, 2018, 60(2): 362–367. doi: 10.1109/TEMC.2016.2621884
[12] LIU Z, WANG X C. FDTD numerical calculation of shielding effectiveness of electromagnetic shielding fabric based on warp and weft weave points[J]. IEEE Trans-actions on Electromagnetic Compatibility, 2020, 62(5): 1693–1702. doi: 10.1109/TEMC.2019.2947133
[13] FELIZIANI M. A FEM approach to shielding effectiveness in braided-shield cables[J]. IEEE Transactions on Magnetics, 1990, 26(2): 929–932. doi: 10.1109/20.106470
[14] HASSELGREN L, MOLLER E, HAMNERIUS Y. Calculation of magnetic shielding of a substation at power frequency using FEM[J]. IEEE Transactions on Power Delivery, 1994, 9(3): 1398–1405. doi: 10.1109/61.311168
[15] MADDAH-ALI M, SADEGHI S H H, DEHMOLLAIAN M. Efficient method for calculating the shielding effectiveness of axisymmetric multilayered composite enclosures[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(1): 218–228. doi: 10.1109/TEMC.2019.2894989
[16] NAZARI M, MOINI R, FORTIN S, et al. On the performance of grounding, bonding, and shielding systems for direct and indirect lightning strikes[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(1): 135–143. doi: 10.1109/TEMC.2018.2885965
[17] PIENAAR H, READER H C, DAVIDSON D B. Karoo array telescope berm shielding: efficient computational modeling and multicopter measurement[J]. IEEE Transactions on Electromagnetic Compatibility, 2017, 59(2): 375–382. doi: 10.1109/TEMC.2016.2618911
[18] YUAN H B, BAO W T, LEE C H, et al. A method of moments wide band adaptive rational interpolation method for high-quality factor resonant cavities[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(5): 3595–3604. doi: 10.1109/TAP.2022.3142281
[19] CHEN K, DU P A, NIE B L, et al. An improved MOM approach to determine the shielding properties of a rectangular enclosure with a doubly periodic array of apertures[J]. IEEE Transactions on Electromagnetic Compatibility, 2016, 58(5): 1456–1464. doi: 10.1109/TEMC.2016.2574739
[20] ARANEO R, CELOZZI S. Toward a definition of the shielding effectiveness in the time-domain[C]//2013 IEEE International Symposium on Electromagnetic Compatibility. Denver, CO, USA: IEEE, 2013: 113–117.
[21] CELOZZI S, ARANEO R. Alternative definitions for the time-domain shielding effectiveness of enclosures[J]. IEEE Transactions on Electromagnetic Compatibility, 2014, 56(2): 482–485. doi: 10.1109/TEMC.2013.2282713
[22] TATEMATSU A, RACHIDI F, RUBINSTEIN M. Analysis of electromagnetic fields inside a reinforced concrete building with layered reinforcing bar due to direct and indirect lightning strikes using the FDTD method[J]. IEEE Transactions on Electromagnetic Compatibility, 2015, 57(3): 405–417. doi: 10.1109/TEMC.2015.2400132
[23] CAO L, XIE Y Z, GAO M X. Analysis of time-domain shielding effectiveness of enclosures above lossy half-space using an improved half-space FDTD method[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(5): 2076–2083. doi: 10.1109/TEMC.2020.2964267
[24] FAN K H, WEI B, HE X B. A subgridding unconditionally stable FETD method based on local eigenvalue solution[J]. IEEE Transactions on Antennas and Propaga-tion, 2021, 69(8): 4695–4705. doi: 10.1109/TAP.2020.3048503
[25] CHEN K, LIU J, ZHUANG M W, et al. New mixed SETD and FETD methods to overcome the low-frequency breakdown problems by tree-cotree splitting[J]. IEEE Transactions on Microwave Theory and Techniques, 2020, 68(8): 3219–3228. doi: 10.1109/TMTT.2020.2995721
[26] CHEN K, HOU X Y, ZHUANG M W, et al. An efficient mixed finite-element time-domain method for complex electrically small problems[J]. IEEE Transactions on Microwave Theory and Techniques, 2019, 67(4): 1285–1294. doi: 10.1109/TMTT.2019.2899842
[27] BERNARD L, TORRADO R R, PICHON L. Efficient implementation of the UPML in the generalized finite-difference time-domain method[J]. IEEE Transactions on Magnetics, 2010, 46(8): 3492–3495. doi: 10.1109/TMAG.2010.2045357
[28] ANDERSEN L S, VOLAKIS J L. Hierarchical tangential vector finite elements for tetrahedra[J]. IEEE Microwave and Guided Wave Letters, 1998, 8(3): 127–129. doi: 10.1109/75.661137
[29] WEBB J P. Hierarchal vector basis functions of arbitrary order for triangular and tetrahedral finite elements[J]. IEEE Transactions on Antennas and Propagation, 1999, 47(8): 1244–1253. doi: 10.1109/8.791939
[30] GEDNEY S D, KRAMER T, LUO C, et al. The discontinuous Galerkin finite element time domain method (DGFETD)[C]//2008 IEEE International Symposium on Electromagnetic Compatibility. Detroit, MI, USA: IEEE, 2008: 1–4.
[31] GEDNEY S D. An anisotropic PML absorbing media for the FDTD simulation of fields in lossy and dispersive media[J]. Electromagnetics, 1996, 16(4): 399–415. doi: 10.1080/02726349608908487
[32] MONTSENY E, PERNET S, FERRIÉRES X, et al. Dissipative terms and local time-stepping improvements in a spatial high order discontinuous Galerkin scheme for the time-domain Maxwell's equations[J]. Journal of Computational Physics, 2008, 227(14): 6795–6820. doi: 10.1016/j.jcp.2008.03.032
[33] COHEN G, FERRIERES X, PERNET S. A spatial high-order hexahedral discontinuous Galerkin method to solve Maxwells equations in time domain[J]. Journal of Computational Physics, 2006, 217(2): 340–363. doi: 10.1016/j.jcp.2006.01.004
[34] LIN C P, YAN S, ARSLANBEKOV R R, et al. A DGTD algorithm with dynamic h-adaptation and local time-stepping for solving Maxwell's equations[C]//2016 IEEE International Symposium on Antennas and Propagation (APSURSI). Fajardo, PR, USA: IEEE, 2016: 2079–2080.
[35] FEZOUI L, LANTERI S, LOHRENGEL S, et al. Convergence and stability of a discontinuous Galerkin time-domain method for the 3D heterogeneous Maxwell equations on unstructured meshes[J]. ESAIM: Mathematical Modelling and Numerical Analysis, 2005, 39(6): 1149–1176. doi: 10.1051/m2an:2005049
[36] POSPIŠEK T, KONEČNY D. METIS[CP]// Berlin, Heidelberg: Springer, 2010.
[37] ARANEO R, LOVAT G, PAULOTTO S. Effects of aperture thickness on the shielding effectiveness of metallic enclosures[C]//2007 IEEE International Symposium on Electromagnetic Compatibility. Honolulu, HI, USA: IEEE, 2007: 1–3.
[38] LI M, NUEBEL J, DREWNIAK J L, et al. EMI from air-flow aperture arrays in shielding enclosures-experiments, FDTD, and MoM modeling[J]. IEEE Transactions on Electromagnetic Compatibility, 2000, 42(3): 265–275. doi: 10.1109/15.865333
计量
- 文章访问数: 650
- HTML全文浏览量: 74
- PDF下载量: 71
