0.   引　言

操纵性是体现水下航行体水动力性能的重要方面，而艉操纵面的布局选型与设计是影响操纵性的重要因素。关于X形艉水下航行体的操纵性水动力特性，国内外学者近年来开展了不少研究。

例如，MaCkay^[1]整理了1987～1988年期间有关十字形和X形艉水下航行体缩比艉段风洞模型的试验结果，但公开的试验数据分析及结论极少。该研究中开展的压力测量试验仅针对艉操纵面，未考虑艉段表面，尤其是与艉附体紧邻的主体表面。Bettle^[2]采用经验公式与数值模拟相结合的方法，对不同X形艉舵面积方案的水下航行体操纵性能进行了预报，但在文中未提及姿态角对舵水动力影响的评估。Broglia等^[3]针对不同面积的十字形和X形艉水下航行体在深水及近水面时水平面内非定常PMM运动的水动力进行了数值模拟，并对比评估了两个方案的稳定性，但未对与舵角相关的水动力特性进一步开展深入分析。国内学者也针对X形艉水下航行体的操纵性展开了相关研究^[4-10]。

综上所述，由X形艉水下航行体操纵性水动力特性研究现状可知：涉及X形艉布局方案的水下航行体变舵角及其姿态角耦合下的水动力特性分析不多。由于此研究是采用数学模型预报X形艉布局的水下航行体操纵运动的重要组成部分，因此，计及姿态角影响来开展X形艉水下航行体舵角水动力特性的研究具有重要意义。

本文将针对基于SUBOFF模型的X形艉布局改型方案，通过数值计算分析该布局方案下变单舵、变单舵耦合攻角和漂角时的操纵性水动力特性，按照现有的船标推荐的公式^[11]，对姿态角耦合下的变舵角水动力特性进行拟合研究，用以为X形艉水下航行体的操控及仿真评估提供支撑。

1.   数值计算简介

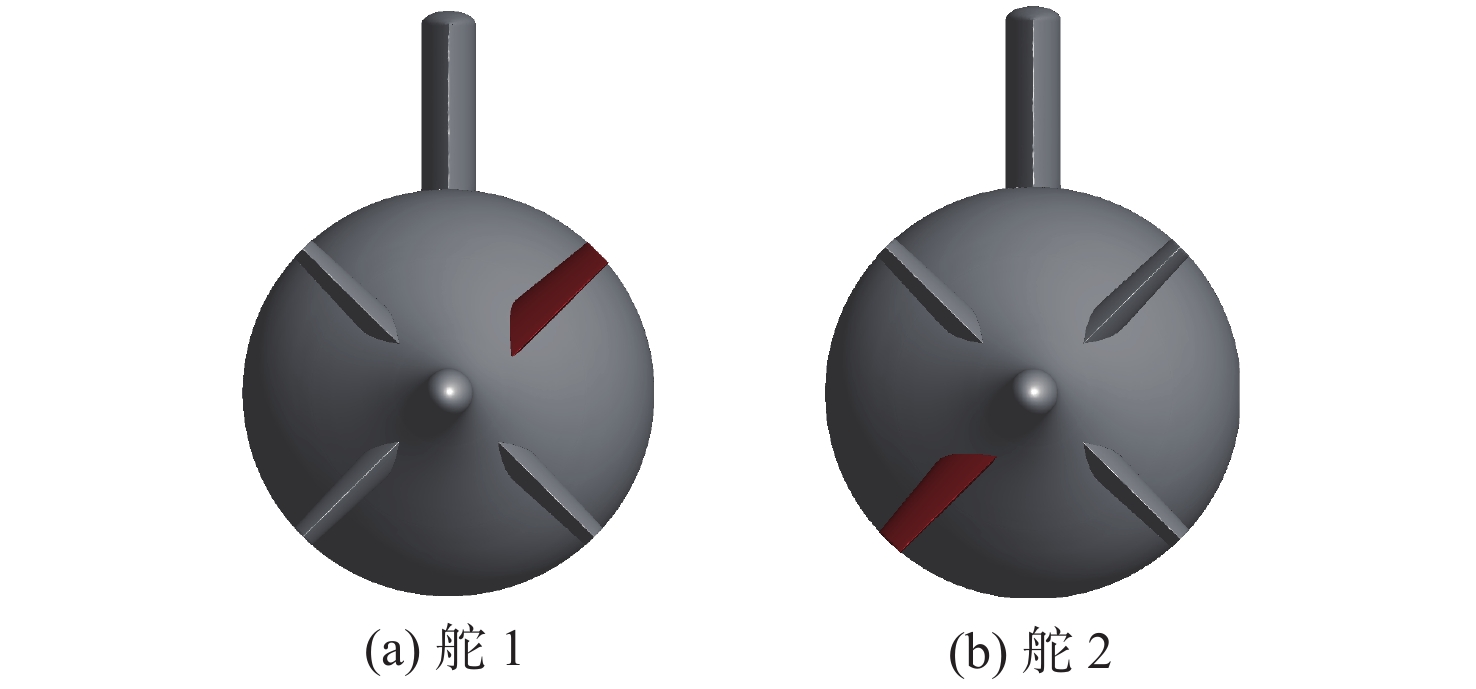
研究对象为基于SUBOFF模型的改型，如图1所示。其由主体、围壳及艉操纵面（4个全动舵，由SUBOFF十字形方案旋转45°得到）构成，其中不含导管及支柱。表1给出了主要参数^[12]。

图  1  SUBOFF潜艇模型

Figure  1.  SUBOFF submarine model

下载: 全尺寸图片 幻灯片

表  1  研究对象主要参数

Table  1.  Main parameters of SUBOFF submarine model

参数	数值
垂线间长Lpp /m	4.261
坐标原点距艏纵向距离x/m	2.013
坐标原点距基线垂向距离z/m	0.254
舵轴距舵尾缘纵向距离xR/m	0.137
舵面积S/m2	0.025
展弦比λ	0.720

下载: 导出CSV 

| 显示表格

1.1   X舵舵角定义

图2给出了本文计算所涉及的舵1及舵2正舵角定义。各舵尾缘朝下偏转为正，主体攻角、漂角及其侧向力Y、垂向力Z、俯仰力矩M、偏航力矩N按照通用艇体坐标系定义^[13]。

图  2  X舵正舵角定义

Figure  2.  Definition of X-rudder angle

下载: 全尺寸图片 幻灯片

1.2   计算策略及数据处理

本文数值研究的计算域、网格生成参数、边界条件定义等与文献[9]中的计算策略完全一致。针对SUBOFF的操纵性水动力计算，已将文献[9]与文献[12]的模型试验结果进行了验证，这里不再赘述。

数值计算的操纵性水动力/矩按通用艇体坐标系表达^[13]，并按式（1）～式（4）无因次化。

式中：$\rho$为流体介质密度；$U$为入口合速度。

2.   计算结果及分析

2.1   变单舵操纵性水动力特性

由于舵角超过一定值后可能会出现失速现象，为了使计算研究结论具有一定的普适性，并考虑到研究对象舵展弦比较小，因此确定本次计算分析时姿态角耦合舵角δ最大为10°。

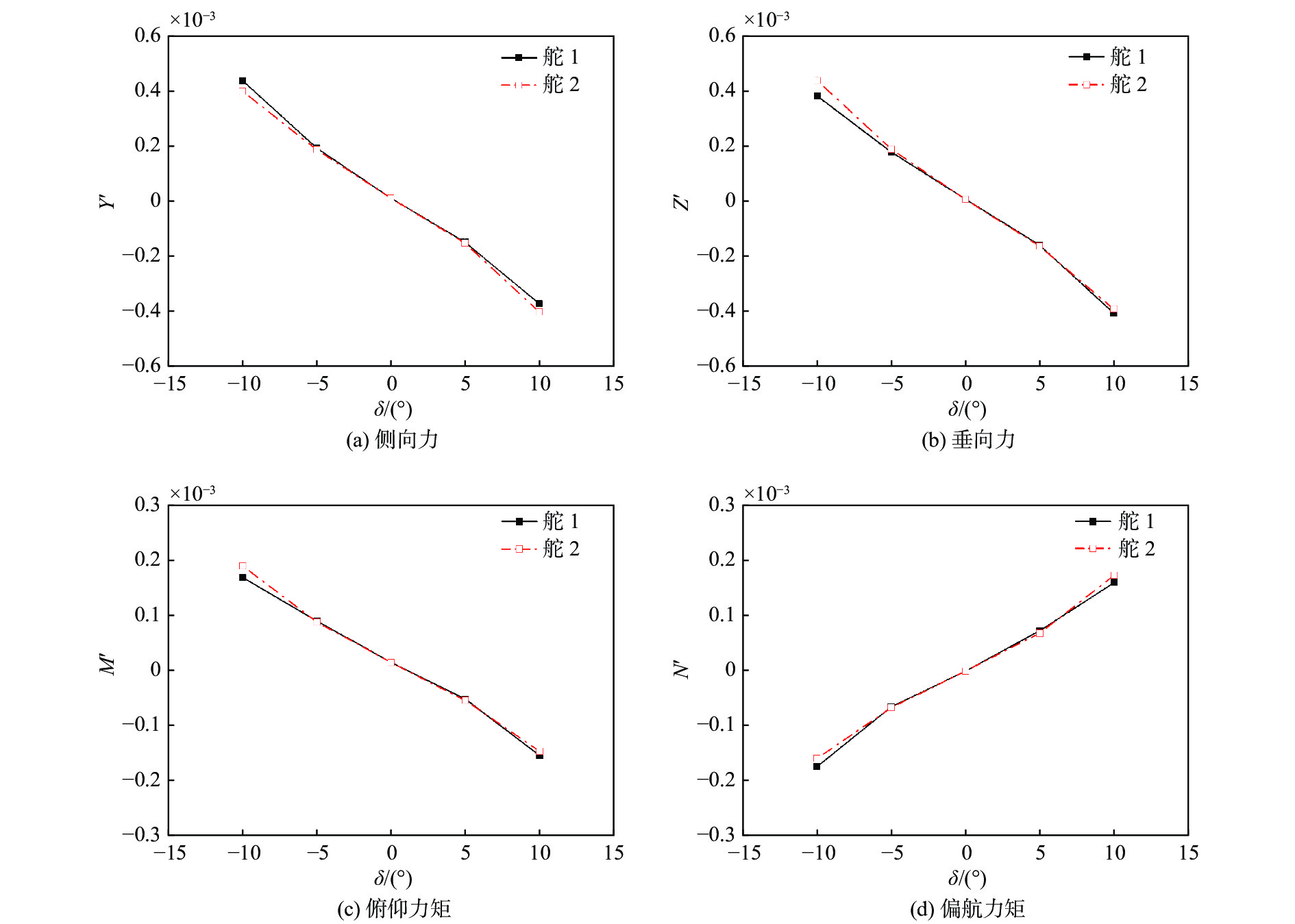
首先，针对舵1和舵2开展变单舵的操纵性水动力计算，舵角δ变化范围为−10°～+10°，Δδ = 5°，如图3所示。由图可见，舵1和舵2的舵角增大时，整体操纵性水动力/矩分量呈单调变化。需要注意的是：在同一舵角下，水平面和垂直面内的水动力分量（Y′与Z′）、矩分量（M′与N′）并不是简单地按照45°分解成相同的两个分量； 在10°舵角时，两者存在着较大差异；在舵角相同及符号相反时，同一方向的水动力/矩分量也存在明显的差异。以舵1的舵角 δ₁ = ±10°的水动力为例，表2给出了各部件的操纵性水动力量值对比，以进一步分析产生上述差异的原因。

图  3  变单舵数值计算结果

Figure  3.  Computational results of single rudder variation

下载: 全尺寸图片 幻灯片

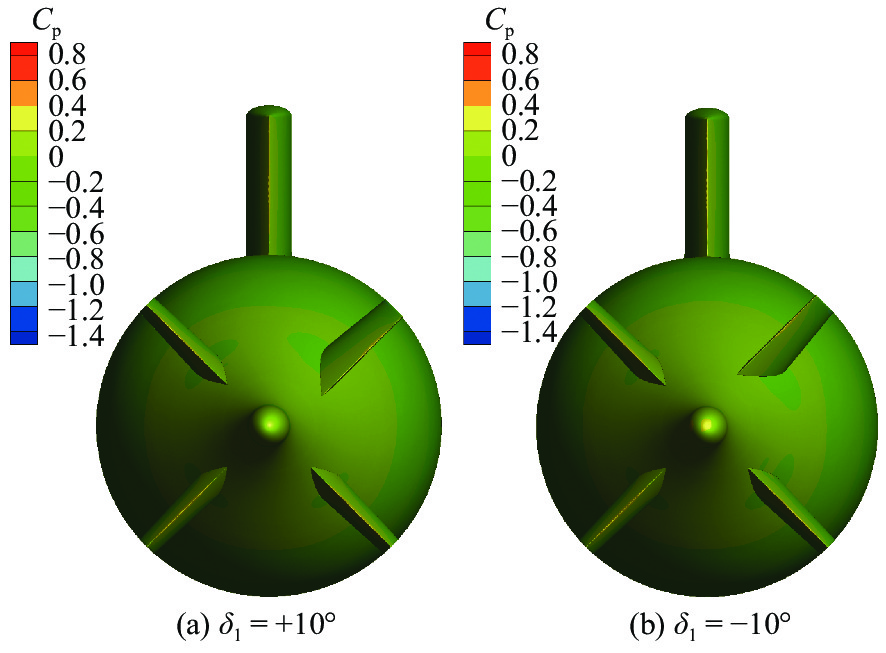
表  2  潜艇各部件水动力对比

Table  2.  Comparison of hydrodynamic forces on each part of submarine

δ1/(°)	位置力	主体	围壳	舵1	舵2	右下舵	左上舵	合计
−10	1 000Y′	0.194	0.005	0.230	0.011	0.019	−0.032	0.427
10		−0.145	0.004	−0.216	−0.016	−0.016	0.010	−0.378
−10	1 000Z′	0.402	−0.251	0.223	0.012	−0.022	0.016	0.380
10		0.069	−0.251	−0.223	−0.007	0.024	−0.017	−0.406

下载: 导出CSV 

| 显示表格

考虑到受围壳影响，垂向力在各舵角为0时存在零升力。因此，为更好地分析对称舵角所引起的非对称力，此处仅对δ₁ = ±10°的侧向力进行分析。由表2中加粗数值可见：当舵1的舵角相同但符号相反时，除舵1外，主体上的水动力差异较为明显，其他部件力基本不变（相较主体差了一个量级甚至更多）。图4分别给出了两个舵角时艉部压力系数C_p的云图对比。由图4可见，在δ₁ = +10°时，主体位于舵1的吸力面侧产生了较大的低压区。由于该低压区位于舵1上侧，从投影面上看，该低压区在垂直面的贡献要高于水平面，即主体在水平面产生的侧向力较小；反之，在δ₁ = −10°时，低压区位于舵1下侧方向，同样根据投影，该低压区在水平面的贡献要高于垂直面，即主体在水平面产生的侧向力较大。由表2中统计的合力结果可见，在δ₁ = −10°时，产生的侧向力较δ₁ = +10°时增大了近13%。综上，产生上述差异的原因是有舵角时舵与主体艉部间的相互作用在水平面、垂直面两个正交平面内不同所致。

图  4  变单舵时艉部压力云图比较

Figure  4.  Comparison of pressure contours on the afterbody for single rudder variation

下载: 全尺寸图片 幻灯片

2.2   计及攻角的变舵角操纵性水动力特性

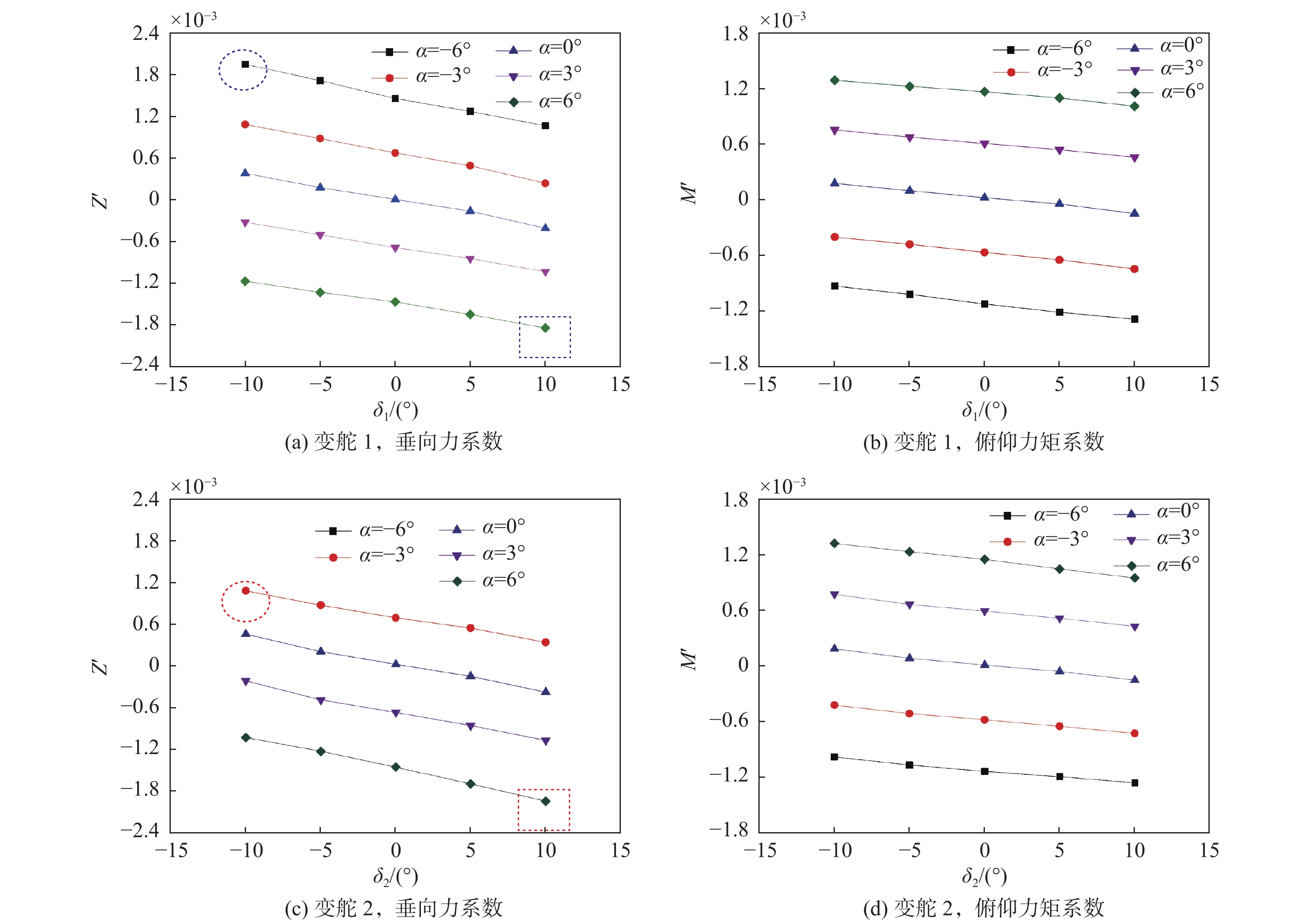
为进一步计算舵1和舵2在不同攻角下的变舵角操纵性水动力数值，设攻角α变化范围为−6°～+6°，得到如图5所示各工况下的垂向力、俯仰力矩结果。通过对攻角耦合舵角的操纵性水动力数据分析可知：

图  5  不同攻角下变单舵的数值计算结果

Figure  5.  Computational results of single rudder variation at different attack angles

下载: 全尺寸图片 幻灯片

1） 因航行体零升力和零俯仰力矩较小，在舵1和舵2的角度均为0°时，其垂向力系数、俯仰力矩系数量值基本上是关于攻角反对称的。

2） 攻角耦合舵1或舵2后的水动力不是反对称的，在正、负舵角时呈现出了差异。以舵1耦合攻角后的垂向力系数为例，如图5（a）蓝色线框所示，此处产生差异的原因是，变舵1时舵与主体艉部间的相互作用在水平面、垂直面不同。更重要的是，此处还包含了航行体攻角对舵力的影响：有别于负攻角，对于正攻角，舵1处于主体尾流之中； 此时，舵升力特性较弱，导致了位置力（矩）较小。

3） 对比舵1和舵2耦合攻角后的水动力特性可知，两种工况也存在差异，如图5（a）和图5（c）中相同形状的线框所示。同样，以舵角−10°、攻角−6°时为例，变舵1对应的垂向力系数较大，变舵2对应的垂向力系数较小，这是主体尾流造成舵1和舵2升力特性存在差异所致。

为定量评估攻角变化对舵1和舵2水动力特性的影响，分别对两者在不同攻角下的舵导数进行拟合，结果如表3及图6所示。

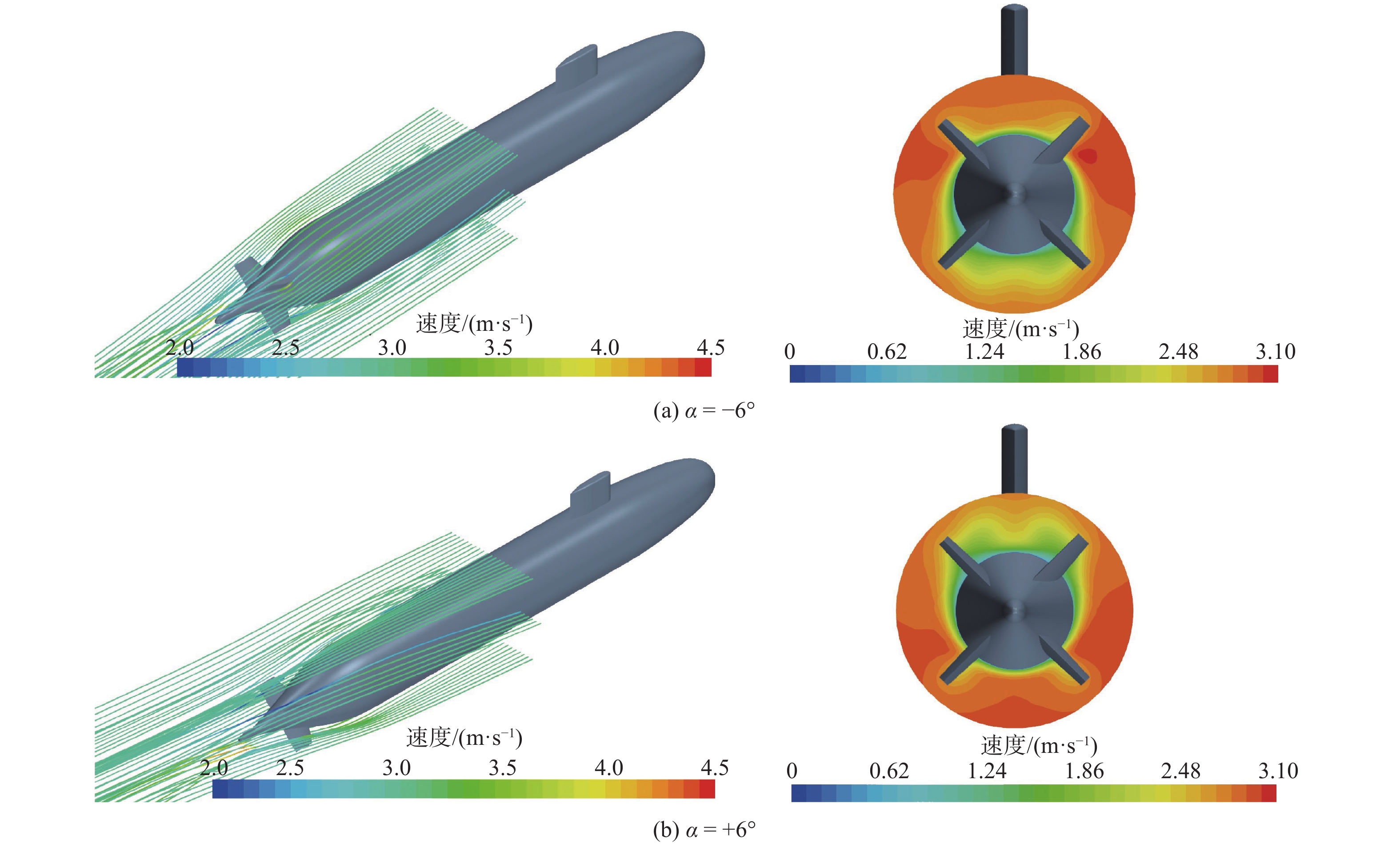
表  3  舵1和舵2在不同攻角下的舵导数

Table  3.  Rudder derivatives of rudder-1 and rudder-2 at different attack angles

舵	$Z_\delta '$						${ {M} }_\delta '$
	α = −6°	α = −3°	α = 0°	α = 3°	α = 6°		α = −6°	α = −3°	α = 0°	α = 3°	α = 6°
δ1	−2.528	−2.380	−2.197	−2.021	−1.899		−1.036	−0.979	−0.902	−0.827	−0.777
δ2	−1.905	−2.069	−2.308	−2.373	−2.636		−0.782	−0.850	−0.933	−0.969	−1.064

下载: 导出CSV 

| 显示表格

图  6  舵导数随攻角变化曲线

Figure  6.  Variation of rudder derivatives with attack angles

下载: 全尺寸图片 幻灯片

由表3及图6可见，攻角增大使得舵1、舵2的舵效（力、矩导数）分别呈减小和增大的趋势。相比无攻角时的舵导数，其相对变化的最大量值达15%。图7以固定 δ ₁ = −10°为例，给出了攻角为−6°和+6°时的表面速度场流线图（左）及舵前方剖面的速度场云图（右）。

图  7  攻角±6°时舵1附近流线及速度场云图

Figure  7.  Streamlines and velocity contours around rudder-1 at ±6° of attack angle

下载: 全尺寸图片 幻灯片

从图7的结果对比可见，有别于−6°攻角，在+6°攻角时，舵1被主体尾流包围，流速呈现较明显的低速状态。因此，在此尾流中系列变舵角的舵效会明显低于−6°攻角状态。与此类似，舵2只是在正攻角时处于迎流端，使得舵效高于负攻角状态。这解释了图6中舵1和舵2的舵效随攻角的变化呈现不同趋势的原因。

进一步地，为更好地对水下航行体操纵运动进行预报仿真，按照现有船标推荐公式^[11]，对舵1和舵2与攻角耦合的水动力导数量值进行了回归分析，拟合公式如下：

式中： i = 1，2；F代表各舵的水动力（矩）分量，即Z，M；w为无因次化的垂向速度。按此线性拟合的各系数如表4所示。

表  4  变攻角耦合变舵角水动力系数整体拟合

Table  4.  Fitting of hydrodynamic coefficients of single rudder coupling with attack angle

水动力系数	量值
	Z′相关	M′相关
$F_0'$	−0.001×10−3	0.0120×10-3
$F_w'$	−13.950×10−3	10.880×10−3
$F_{\delta_1}'$	−2.205×10−3	−0.904×10−3
$F_{w\delta_1}'$	3.085×10−3	1.280×10−3
$F_{\delta_2}'$	−2.258×10−3	−0.920×10−3
$F_{w\delta_2}'$	−3.375×10−3	−1.305×10−3

下载: 导出CSV 

| 显示表格

由表4可见，拟合的舵1和舵2的线性导数$F_{{\delta _i}}'$符号相同、量值相当，但攻角与舵角相关的耦合导数$F_{w \delta_{t}}^{\prime}$符号是不同的，这与图6中两舵舵导数随攻角变化关系不同是一致的。

2.3   计及漂角的变舵角操纵性水动力特性

与攻角计算工况类似，分别计算舵1和舵2在不同漂角下的变舵角操纵性水动力数值，设漂角β变化范围为−6°～+6°，得到如图8所示各工况下的计算结果。

图  8  不同漂角下变单舵的数值计算结果

Figure  8.  Computational results of single rudder variation for different drift angles

下载: 全尺寸图片 幻灯片

由图8可见，对于漂角与舵1和舵2耦合的操纵性水动力特性而言，其与变攻角类似，这里不再赘述。

同样地，为定量评估不同漂角下舵1和舵2的舵效，分别对两者在不同漂角下的舵导数进行拟合，结果如表5和图9所示。

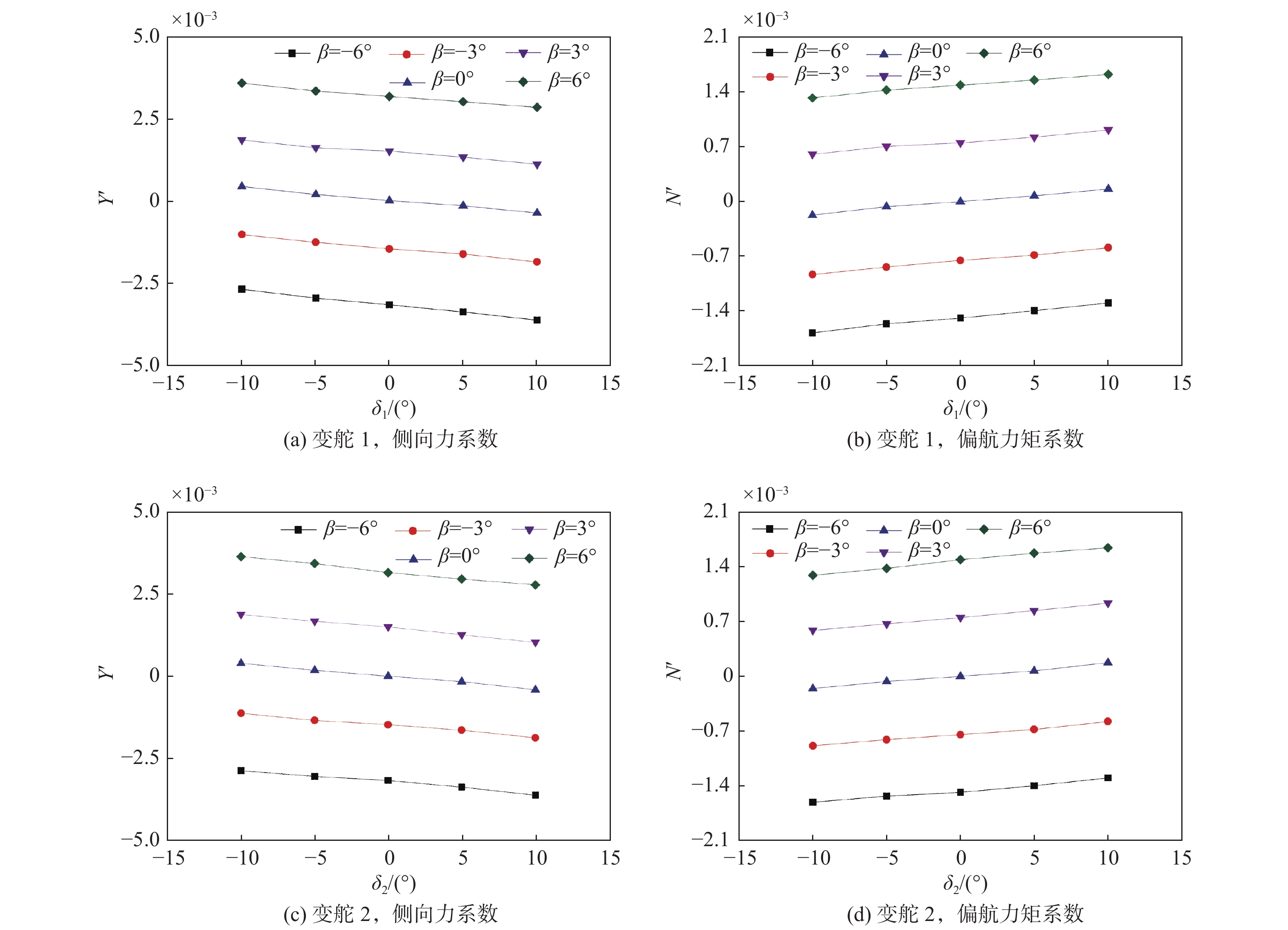
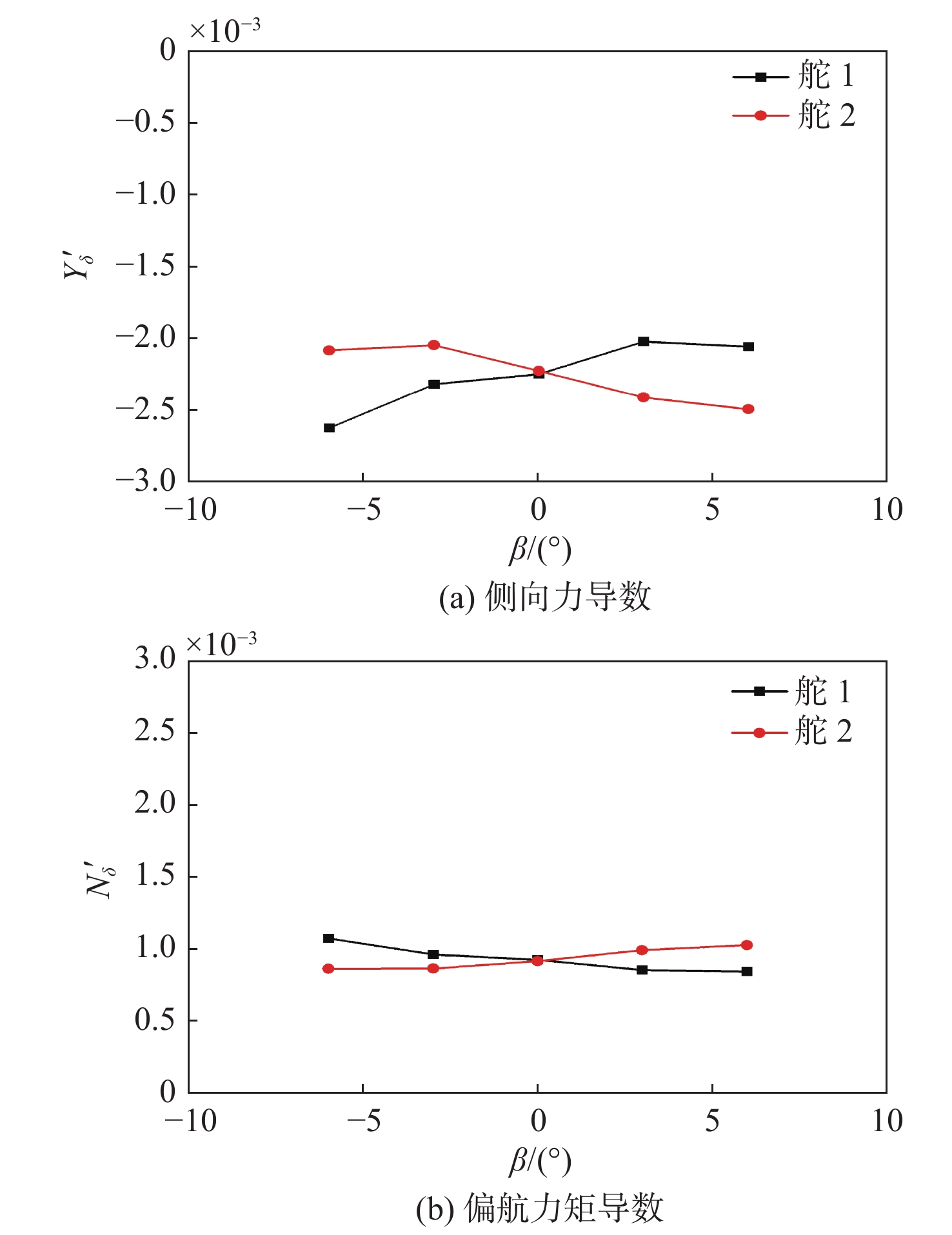
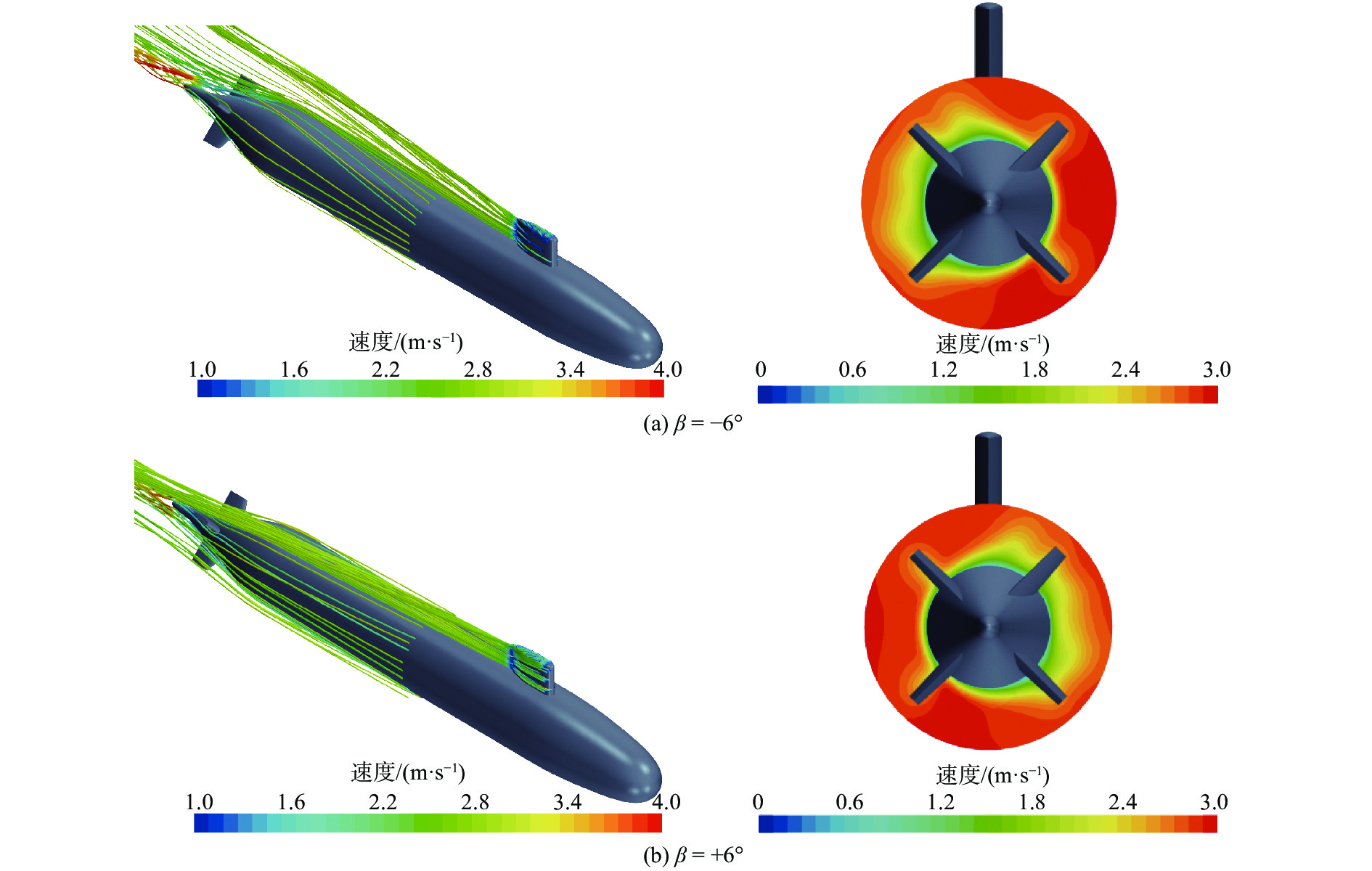
表  5  舵1和舵2在不同漂角下的舵导数

Table  5.  Rudder derivatives of rudder-1 and rudder-2 at different drift angles

舵	$Y_\delta '$						${{N} }_\delta '$
	β = −6°	β = −3°	β = 0°	β = 3°	β = 6°		β = −6°	β = −3°	β = 0°	β = 3°	β = 6°
δ1	−2.624	−2.319	−2.247	−2.022	−2.058		1.071	0.959	0.922	0.851	0.842
δ2	−2.083	−2.046	−2.225	−2.411	−2.493		0.861	0.863	0.914	0.990	1.025

下载: 导出CSV 

| 显示表格

图  9  舵导数随漂角变化曲线

Figure  9.  Curves of rudder derivatives related with drift angles

下载: 全尺寸图片 幻灯片

由表5和图9可见，随着漂角的增大，舵1和舵2的舵效（力、矩导数）分别呈减小和增大的趋势。相比于无漂角的情况，舵效相对变化的最大量值达16%。图10以δ₁ = −10°为例，给出了漂角为−6°和+6°时的表面速度场流线图（左）及速度场云图（右）。

图  10  漂角±6°时舵1附近流线及速度场云图

Figure  10.  Streamlines and velocity contours around rudder-1 at ±6° of drift angle

下载: 全尺寸图片 幻灯片

从图10的结果对比可见，有别于−6°漂角，在+6°漂角时，舵1被主体尾流包围，流速呈现较明显的低速状态。此外，围壳根部的低速尾流也影响了舵1的表面流动状态，因此在此尾流中系列变舵角的舵效会明显低于负漂角状态。舵2与之类似，只是在正漂角时，舵2处于迎流端，使得舵效高于负漂角情况。这解释了图9中舵1与舵2的舵效存在差异的原因。

同样地，为更好地对水下航行体操纵运动进行预报仿真，对舵1和舵2与漂角耦合的水动力导数量值进行了回归分析，拟合公式如下：

式中： i =1，2；F代表各舵的水动力（矩）分量，即Y，N；v为无因次化的横向速度。按此线性拟合的各系数如表6所示。

表  6  变漂角耦合变舵角水动力系数整体拟合

Table  6.  Fitting of hydrodynamic coefficients of single rudder coupling with drift angle

水动力系数	量值
	Y′相关	N′相关
$F_0'$	0	0
$F_v'$	−29.840×10−3	−14.210×10−3
$F_{\delta_1}'$	−2.254×10−3	0.929×10−3
$F_{v\delta_1}'$	−2.727×10−3	1.082×10−3
$F_{\delta_2}'$	−2.252×10−3	0.930×10−3
$F_{v\delta_1}'$	2.264×10−3	−0.871×10−3

下载: 导出CSV 

| 显示表格

由表6可见，舵1和舵2漂角相关舵导数符号不同，这与图9中两舵舵导数随漂角变化关系不同是一致的。

3.   结　论

本文以基于SUBOFF潜艇模型的X形艉布局为研究方案，采用经过验证的数值计算方法分析了变单舵、变单舵耦合攻角及变单舵耦合漂角时的操纵性水动力特性，并按照现有船标推荐公式，对姿态角耦合下的变舵角水动力特性进行了拟合研究。主要研究结论如下：

1） 变单舵时，同一舵角下水平面和垂直面内的水动力分量（Y′与Z′）、矩分量（M′与N′）存在差异；当舵角角度相同及符号相反时，同一方向的水动力（矩）量值存在明显差异。上述现象在大舵角时尤为明显。经分析，上述差异是由于X舵与主体艉部间存在相互作用，使得在垂直面、水平面内的投影不同所导致。

2） 无姿态角时的X舵舵效与耦合姿态角后的X舵舵效差异较大。在本文研究的姿态角及舵角范围内，舵1和舵2的舵效分别随攻角/漂角的增大而呈减小和增大的趋势。无姿态角时的舵导数相对变化量值最大达16%。经分析典型工况下的流场可知，两舵舵效呈不同趋势变化是由于不同姿态角下的主体尾流影响了舵表面流动所致。

3） 按照现有船标推荐公式拟合获得的舵1和舵2舵角、姿态角耦合的水动力（矩）导数量值与各自的线性导数相当，且舵1和舵2的耦合导数符号相反，这与主体姿态角的影响密切相关。

上述结论可为与X形艉水下航行体变舵角相关的操纵运动数学建模以及操纵性分析提供技术支撑，分析方法适用于X形艉布局的水下航行体变双舵或四舵的情形。后续工作中，建议对主体艉部及舵表面的压力测试进行分析以进一步验证结论1）。